---
title: 'The Fermat''s principle F'
media_order: stationnarite3_650.jpg
published: false
routable: false
visible: false
---

!!!! *IN  CONSTRUCTION !*
!!!!
!!!! *very imperfect course,*
!!!i *not validated by the teaching team*

-------------

### Fundamentals of geometric optics

#### Geometric optics: <br> a simple physical model.

Its *fundamentals* are:
* The concept of **light ray** : oriented trajectory of light energy
* The concept of **refractive index** : characterizes the apparent speed of light in a homogeneous medium
* The **Fermat's principle**

##### Ray of light

![](rays_forest.jpg)

<!--For the audio:
Walking in the forest on a hot summer day is a huge pleasure. The contrast between the freshness of the shaded parts by the foliage and the tree trunks, and the heat in the direct sunlight is striking. The beams of direct light increase the temperature of the air, making you sweat, and hit your skin giving you this slight sensation, not unpleasant because mastered, burning. The light carries energy .... As you walk, you can anticipate, hurry to the arrival of a shaded area, because the play of light with the trees zebra the space around you. In the air with the unique and wonderful scents of the forest, the rays of light propagate in straight lines, they follow the path of propagation of the luminous energy .-->

[AUDIO : _the intuition of the "ray of light" during a walk in the forest_](OG_rayons_foret.mp3)

The **light rays** are *oriented lines* that in each of their points indicate the *direction of propagation of the luminous energy*.

The light rays follow *straight lines in a homogeneous medium*.

Light rays *do not interact with each other*

##### The refraction index

**Refractive Index $`n`$** &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
**$`n \; = \; \dfrac{c}{v}`$**
* **`c`** : *speed of light in vacuum* (absolute limit)
* **`v`** : *speed of light in the middle* homogeneous

**$`\Longrightarrow \: : \: n`$** : physical dimension **without dimension** and **always > 1**.

Dependency : **$`n \; = \; n (\nu) \; \; \; `$**, or **$` \; \; \; n \; = \; n (\lambda_0) \; \ ; \; `$** *(with $`\lambda_0`$ wavelength in vacuum)*

<!--
I wanted to make this important remark here, but it is not simple: with Doppler effect, medium of propagation does not move with respect to the observer ... I must think to make the warning in the main text, and a summary of all this in for example a parallel 1:

!!!! ATTENTION: the $`\nu`$ frequency of a wave (temporal magnitude) measured by a given observer does not depend on the propagation 
!!!! medium in which the measurement takes place. This is not the case of the measured wavelength $`\lambda`$, which depends on the propagation medium because the propagation speed of the $V$ wave may depend on this medium. Frequency, wavelength and speed of propagation of a wave are related
!!!! by the equation $'\lambda\;=\;\dfrac{V}{\nu}'$, but : <br>
!!!! the **fundamental quantity** (independent of the middle) is the **frequency $`\nu`$ (the temporal magnitude)**.
-->

!! TO GO FURTHER :
!!
!! over the entire electromagnetic spectrum and for any medium:
!! $`n`$: complex value dependent on the $\nu$ frequency of the electromagnetic wave, strong variations representative of all light / matter interaction mechanisms: $`n (\nu) = \Re[n(\nu )] + \Im[n(\nu)]`$ <br>
!!
!! In the visible domain (where $`\lambda_0`$ is more used than $`\nu`$) and for transparent medium : <br>
!! real value, small variations of $`n`$ with $`\lambda_0`$ $`\left(\frac{\Delta n}{n} < 1\%\right)`$

##### Optical path

**optical path** *$`\delta`$* &nbsp;&nbsp;&nbsp;&nbsp; $`=`$
**euclidean length** *$`s`$* &nbsp;&nbsp;&nbsp; $`\times`$ &nbsp;&nbsp; **refractive index** *$`n`$*

* **$`\Gamma`$** : *path (solid line) between 2 fixed points A and B*
* **$`\mathrm{d}s_P`$** : *element of infinitesimal length at point P on path $`\Gamma`$*
* **$` n_P`$** : *refractive index at point P*
* **$`\mathrm{d}\delta_P`$** : *infinitesimal optical path at point P on path $`\Gamma`$*

Optical path along a path between 2 fixed points A and B :
**$`\delta\;=\;\displaystyle\int_{P \in \Gamma}\mathrm{d}\delta_P\;`$$`=\;\displaystyle\int_{P \in \Gamma}n_P\cdot\mathrm{d}s_P`$**

* **$`\delta`$** $`=\displaystyle\int_{\Gamma}n\cdot\mathrm{d}s\;=\;\int_{\Gamma}\dfrac{c}{v}\cdot\mathrm{d}s`$ = $`c\;\displaystyle\int_{\Gamma}\dfrac{\mathrm{d}s}{v}`$ = *$`\;c\;\tau`$*
* **$`\delta`$** is *proportional to the travel time*.



#### Optical path

**optical path** *$\delta$* &nbsp;&nbsp;&nbsp;&nbsp; $=$
**euclidean length** *$s$* &nbsp;&nbsp;&nbsp; $\times$ &nbsp;&nbsp; **refractive index** *$n$*

* **$\Gamma$** : *path (solid line) between 2 fixed points A and B*
* **$\mathrm{d}s_P$** : *element of infinitesimal length at point P on path $\Gamma$*
* **$ n_P$** : *refractive index at point P*
* **$\mathrm{d}\delta_P$** : *infinitesimal optical path at point P on path $\Gamma$*

Optical path along a path between 2 fixed points A and B :
**$\delta\;=\;\int_{P \in \Gamma}\mathrm{d}\delta_P\;=\;\int_{P \in \Gamma}n_P\cdot\mathrm{d}s_P$**

* **$\delta$** $=\int_{\Gamma}n\cdot\mathrm{d}s\;=\;\int_{\Gamma}\frac{c}{v}\cdot\mathrm{d}s$ = $c\;\int_{\Gamma}\frac{\mathrm{d}s}{v}$ = *$\;c\;\tau$*
* **$\delta$** is *proportional to the travel time*.


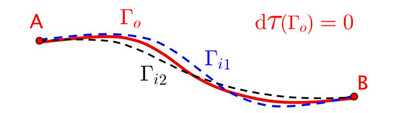
#### Stationarity

* **$\Gamma_o$** : *path between two fixed point A and B*
* **$\lambda_i$** : *parameter that defines a path*
* **${\Large\tau}$** : *grandeur physique caractérisant un chemin*
 
**${\Large\tau}(\Gamma_o)$ stationnaire &nbsp;&nbsp;
${\Longleftrightarrow}\:\:\:\:\:\mathrm{d}{\Large\tau}(\Gamma_o)=\sum_i\frac{\partial{\large\tau}}{\partial\lambda_i}(\Gamma_o)\;\mathrm{d}\lambda_i=0$**

![](stationnarite3_400.jpg)

#### Fermat's principle

**Between two points** of its path, a **ray of light** follows **the path(s)** that present(s) a *stationary travelling time*.

or (equivalent )

**Between two points** of its path, a **ray of light** follows **the path(s)** that present(s) a *stationary optical path*.


#### Examples 

##### Spherical concave mirror

* **A** : *point source* that emits or diffuses lights in all directions.
* **B** : *fixed point in space*.

For this mirror, **according to the positions of points A and B** :

* **several extrema** : here *2 maxima* et *1 minimum* **$\Longrightarrow$ several ligh rays**from A go through B : here *3 rays* :

<!--à finaliser si possible :
1) DIFFICILE : mise au point automatique : largeur 100% de l'écran et bonne hauteur 'difficile cela' de toute application geogebra.
2) TRES DIFFICILE : faire en sorte que en mode connexion, l'image animée correspondante au geogebra s'affiche tant que l'animation iframe geogebra n'est pas téléchargée, puis elle ne s'affiche pas lorsque le geogeba est prêt, et que ce soit elle qui s'affiche en mode "hors connexion".-->

<!--a supprimer
[Click here for geogebra animation](https://www.geogebra.org/material/iframe/id/syegm6gp)
-->

<!--image gif correspondante-->
![](Fermat_mir_3ray_650.gif)

!!!! *Be careful* :<br>
!!!! Understand this example of application of Fermat's theorem. It says that *the 3 trajectories drawn between A and B satisfy the Fermat's principle* and therefore *are possible trajectories between these two points* to the exclusion of any other trajectory. If point A is a point source that emits light in all directions, then these 3 paths will be followed by light. If a ray goes through A with one of these 3 directions, then the corresponding trajectory will be realized.
!!!! *But* the points *A and B are not conjugate points within th meaning of paraxial optics* : B is not the image point of point source A, and vice versa.
!!! It is the same for all the animations of this chapter "examples".

* other positions of A and B : **1 minimum $\Longrightarrow$ 1 unique ray** from A goes trhough B .

![](Fermat_mir_1ray_min_650.gif)

* other positions of A and B : **1 maximum $\Longrightarrow$ 1 unique ray** from A goes trhough B .

![](Fermat_mir_1ray_max_650.gif)

##### Elliptical concave mirror. 

* Elliptical mirror : mirror whose surface is part of an ellipsoid of revolution.

! <details markdown=1>
! <summary>
! Ellipsoid and ellipsoid of revolution
! </summary>
! Est-il nécessaire de rapeller ici ce que sont les ellipsoïde et ellipsoïde de révolution? rappel en texte? ou 2 liens vers Wikipédia? ou lien vers une autre page m3p2 sur les quadriques en géométrie euclidienne (page encore à créer) ? Si oui, dans une partie Beyond, parler du miroir elliptique concave acoustique, c'est impressionnant quand on le vit.
! </details>

* **between the two geometrical foci"** F et F' of an elliptical mirror, **all path are stationary** : they have the same optical path<br>
**$\Longrightarrow$** : *all the rays coming from one of the two foci and intercepting the mirror converge towards the second geometric focus *.

<!-- a supprimer
[Click here for geogebra animation](https://www.geogebra.org/m/aaus5dpr)
-->

![](fermat_mir_elliptique_650.gif)

!!!! *BE CAREFUL* : 
!!! the "geometric foci" of the ellipsoid of revolution, the "geometric surface" in which the surface of the elliptical mirror is inscribed, do not correspond to the optical foci (the two focal points)  of the elliptical mirror as they will be defined in the "optical sense" of the word "focus" in the remainder of this course. 

'The 4 laws of geometrical optics'
---

* **Fermat's principle** *$\Longrightarrow$ the 4 laws of geometrical optics* :

#### Law of reversibility of the path of light.

Optical path and property of stationarity : concept of orientation not used <br>
*$\Longrightarrow$ stationarity property does not depend on the orientation* of the path.

**$\Longrightarrow$**  the **trajectory** *followed by the light* is **indépendant of the direction of propagation along the trajectory**.

#### Law of the rectilinear light trajectory in homogeneous and isotrope media. 

Euclidian space : *straight line = shortest path between 2 points*

**$\Longrightarrow$**  in an **optically homogeneous and isotrope medium**, the *light travels rectilinearly* : the **light rays are straight lines**.

#### The 2 laws of reflection and refraction
! <details markdown=1>
! <summary>
! IF NECESSARY : reminder if the definitions of the angles and refractive indexes used below. 
! </summary>
! $n_{incid}$ : refractive index of the incident light medium.<br>
! $n_{émerg}$ : refractive index of the emergent light medium (so after crossing the surface).<br>
! $i_{incid}$ : incident ray - normal to the surface at the point of impact angle.<br>
! $i_{émerg}$ : emergent ray - normal to the surface at the point of impact angle.<br>
! </details>

For any incident ray impacting a surface :
* The **surface at the point of impact** is *locally a plane*.
* **Plan of incidence** : plane that *contains the incident ray and normal to the surface at the point of impact*.
* **Refracted and reflected rays** are *in the plane of incidence*, on the *side opposite to the incident ray in relation to the normal* at the surface at the impact point.

*Reflection law* : **$i_{réflec} = i_{incid}$**

*Refraction law (Snell-Descartes)* : for any $i_{incid}$  :
* if $\dfrac{n_{incid}}{n_{émerg}}\cdot\sin(i_{incid})\leqslant1$ then **refraction phenomenon** :<br><br>
**$n_{émerg}\cdot sin(i_{émerg})=n_{incid}\cdot sin(i_{incid})$**<br>

* if $\dfrac{n_{incid}}{n_{emerg}}\cdot\sin(i_{incid})>1$ then **total reflection phenomenon** :<br>
*reflected ray* on the interface that follows the reflection law **$i_{réflec} = i_{incid}$**<br>

* **Critical angle** (of inidence) **for total reflection : $i_{incid_limit}=\arcsin\left (\dfrac{n_{émerg}}{n_{incid}}\right)$** *$\Longrightarrow i_{émerg}=\pi/2\:rad = 90 °$*

_Phenomena of reflection and refraction on a refracting surface._

![](interaction_lumiere_surface_3_650.gif)

!! <details markdown=1>
!! <summary>
!! TO GO FURTHER : intensity distribution between reflected and transmitted beam at a refracting surface.
!! </summary>
!! Geometrical optics: does not quantify the reflected $R$ and transmitted $T$ parts of the  incident beam intensity at a plane refracting surface. This distribution varies according to the incidence angle, the polarization of the incident light, the wavelength. This is described by electromagnetism.
!! However a simple result is useful and to know :
!! *The light intensity is either reflected or transmitted* : $R+T=1$.
!!
!! For a light beam of wavelength $\lambda$ of normal incidence upon a refracting surface :
!! - ratio reflected power versus incident power : $R=\left(\dfrac{n_{incid}-n_{émerg}}{n_{incid}+n_{émerg}}\right)^2$
!! - ratio transmitted power versus incident power  : $T=1-R$
!!</details>

_Total reflection phenomenon_

<!--to finalize if possible :
1) DIFFICULT : geogebra animation should spend over 100% of the window width, and keep its correct ratio width / height.
2) VERY DIFFICULT: make sure that in connection mode, the animated image corresponding to the geogebra is displayed as long as the animation iframe geogebra is not downloaded, then it does not appear when the geogeba is ready, and that it is displayed in offline mode".-->

<!--
<!iframe width="auto" height="auto" sandbox="allow-same-origin allow-scripts" src="https://www.geogebra.org/material/iframe/id/bg5ewxee" frameborder="0" allowfullscreen></iframe>

_smartphone : switch to "landscape" mode to see the geogebra animations._
<iframe width="640" height="360" sandbox="allow-same-origin allow-scripts" src="https://www.geogebra.org/material/iframe/id/bg5ewxee" frameborder="0" allowfullscreen></iframe>
<!--image gif correspondante-->

![](Opt_Geo_refle_lim_650.gif)
<!--
animation : https://www.geogebra.org/material/iframe/id/bg5ewxee
-->