---
title: 'The thin lens'
media_order: 'Const_lens_conv_point_AapresO.gif,lens-convergent-N2-en.jpeg,Const_lens_conv_point_AentreFO.gif,lens-convergent-N2-es.jpeg,lens-convergent-N2-fr.jpeg,Const_lens_conv_point_AavantF.gif,lens-divergent-N2-es.jpeg,lens-divergent-N2-fr.jpeg,lens-divergent-N2-en.jpeg,diverging-thin-lens-representation.jpeg,converging-thin-lens-representation.jpeg'
published: true
routable: true
visible: false
lessons:
- slug: simple-optical-elements
- order: 3
---
!!!! *COURS EN CONSTRUCTION :*
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est *en construction*, il n'est *pas validé par l'équipe pédagogique* à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.
--------------------
### What is a lens ?
#### Objective
* initial : to **focuse or disperse the light**.
* ultimate : to **realize images**, alone or as part of optical instruments.
#### Physical principle
* **uses the refractive phenomenon**, described by the Snell-Descartes' law.
#### Constitution
* Piece of **glass, quartz, plastic** (for visible and near infrared and UV).
* **Rotationally symmetrical**.
* **2 polished surfaces** perpendicular to its axis of symmetry, **either or both curved** (and most often spherical).
#### Interest in optics : thin lenses
* **Thin lens** : *thickness << diameter*
* Thins lens : **most important simple optical element** that is *used alone or combined in serie in most optical instruments* : magnifying glasses, microscopes, tele and macro objectives, camera, refracting telescopes.
### Modeling a thin lens surrounded by air, gaz or vaccum.
#### Why modeling ?
* To **understand, calculate and predict images** of objects given by thin lenses
##### Why surrounded by air, gaz or vaccum?
* **In most optical instruments**, lenses are *surrounding by air*.
* **air, gaz and vaccum** have refractive index values in the range "$1.000\pm0.001$, and can be approximated by *$n_{air}=n_{gaz}=n_{vaccum}=1$*
$\Longrightarrow$ same optical behavior in air, gaz and vacuum.
#### Types and characterization of thin lenses
**Convergent** = **converging** = **convexe** = **positive** lenses

* Characterized by :
\- **Focal lenght** (usually in cm) always >0 *+* adjective "**converging**"
or
\- Its **image focal length** $f'$ (in *algebraic value*, usually in cm), that is *positive $f'>0$*.
or
\- Its **vergence** $V$ (in ophtalmology) that is *positive $V>0$*,
with $V (\delta)=\dfrac{1}{f'(m)}$ ($f'$ being expresssed in m "meter" and $V$ in $\delta$ "dioptre", so $\delta=m^{-1}$).
**Divergent** = **diverging** = **concave ** = **negative** lenses

* Characterized by :
\- **Focal lenght** (usually in cm) always >0 *+* adjective "**diverging**"
or
\- Its **image focal length** $f'$ (in *algebraic value*, usually in cm), that is *negative $f'<0$*.
or
\- Its **vergence** $V$ (in ophtalmology) that is *negative $V<0$*,
with $V (\delta)=\dfrac{1}{f'(m)}$ ($f'$ being expresssed in m "meter" and $V$ in $\delta$ "dioptre", so $\delta=m^{-1}$).
### Analytical modeling
(_for thin lens surrounded by air, gaz or vaccum_)
##### Thin lens equation
**$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=V=-\dfrac{1}{\overline{OF}}=\dfrac{1}{\overline{OF'}}$**
##### Transverse magnification expression
**$M_{T-thinlens}=\dfrac{\overline{OA'}}{\overline{OA}}$**
### Graphical modeling
#### Thin lens representation
* **optical axis** = *revolution axis* of the lens, positively *oriented* in the direction of propagation of the light (_from the object towards the lens_).
* **thins lens representation** :
\- *line segment*, perpendicular to optical axis, centered on the axis with symbolic *indication of the lens shape* at its extremities (_convexe or concave_).
\- **S = C = O** : vertex S = nodal point C = center O of the thin lens $\Longrightarrow$ is used point O.
\- *point O*, intersection of the line segment with optical axis.
\- *object focal point F* and *image focal point F'*, positioned on the optical axis symmetrically with respect to the point O ($f=-f'$) at algebraic distances $\overline{OF}=f$ and $\overline{OF'}=f'$.
\- *object focal plane (P)* and *image focal plane (P')*, planes perpendicular to the optical axis at respectively points $F$ and $F'$.
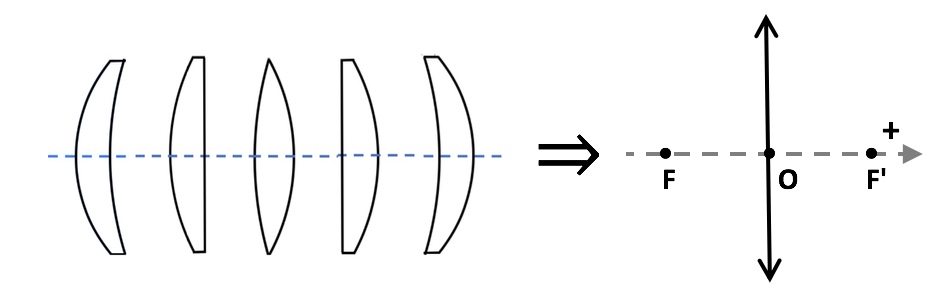
_Converging thin lens representation : $\overline{OF}<0$ , $\overline{OF'}>0$ and $|\overline{OF}|=|\overline{OF'}|$_
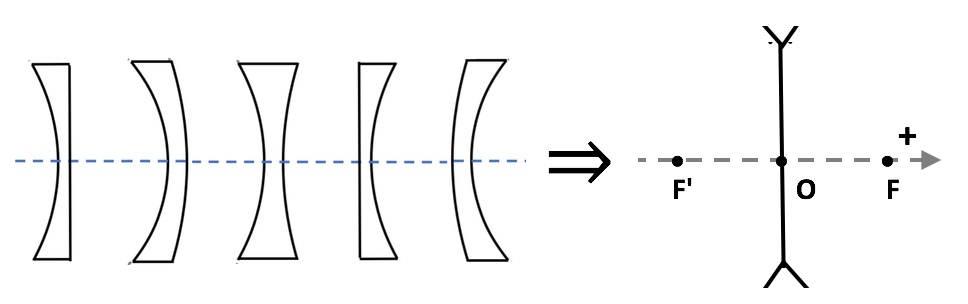
_Divverging thin lens representation : $\overline{OF}>0$ , $\overline{OF'}<0$ and $|\overline{OF}|=|\overline{OF'}|$_
#### Determining conjugate points :
##### Converging thin lens
* **Point source located between ∞ et F**

* **Point source located between F et O**

* **Virtual object point** (will be seen at level foothills, to remove from here).

##### Diverging thin lens
(to be implemented)