---
title: 'La lentille mince'
media_order: 'lens-convergent-N2-en.jpeg,lens-divergent-N2-fr.jpeg,lens-convergent-N2-es.jpeg,lens-convergent-N2-fr.jpeg,lens-divergent-N2-en.jpeg,lens-divergent-N2-es.jpeg'
published: true
routable: true
visible: false
lessons:
- slug: simple-optical-elements
order: 3
---
!!!! *COURS EN CONSTRUCTION :*
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est *en construction*, il n'est *pas validé par l'équipe pédagogique* à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.
---------
### Qu'est-ce qu'une lentille ?
#### Objectif
* premier : **focaliser ou disperser la lumière**.
* ultime : **réaliser des images optiques**, seule ou en tant que composant dans un instrument optique.
#### Principe physique
* **utilise le phénomène de réfraction**, décrit par la loi de Snell-Descartes (loi de la réfraction)
#### Constitution
* réalisé en **verre, quartz, plastique** (pour le domaine visible et proches infrarouge et UV).
* présente une **symétrie de révolution**.
* **2 faces polies** perpendiculaires à son axe de symétrie, **une ou les deux étant courbes** (et le plus souvent la face courbe s'inscrit dans une sphère).
#### Intérêt en optique : les lentilles minces
* **Lentille mince** : *éoaisseur << diamètre*
* Lentille minces : **élément optique simple le plus important** qui est *utilisé seul ou associé en série dans la plupart des instruments optiques* : loupes, microscopes, téléobjectifs et macro-objectifs, appareils photo, lunettes astronomiques et terrestres.
### Modélisation d'une lentille mince plongée dans l'air, un gaz ou le vide.
#### Pourquoi modéliser ?
* Pour **comprendre, calculer et prédire les images** d'objets données par des lentilles minces.
##### Pourquoi plongée dans l'air, un gaz ou le vide ?
* **Dans la plupart des instruments optiques**, les lentilles sont *entourées d'air*.
* **L'air les gaz et le vide** ont des indices de réfraction voisins et proches de "$1.000\pm0.001$, et ils peuvent être approximés par *$n_{air}=n_{gaz}=n_{vaccum}=1$*
$\Longrightarrow$ même comportement optique dans l'air, un gaz et le vide.
#### Types et caractérisations des lentilles minces
**Convergente** = **convexe** = lentille **positive**

Fig. 1. Lentilles convergentes.
* Caractérisée par :
\- **Distance focale** (en général en cm) toujours >0 *+* adjectif "**convergente**"
or
\- Sa **distance focale image** $f'$ (en *valeur algébrique*, en général en cm), qui est *positive $f'>0$*.
or
\- Sa **vergence** $V$ (en ophtalmologie) qui est *positive $V>0$*,
avec $V (\delta)=\dfrac{1}{f'(m)}$ ($f'$ étant exprimée en m "mètre" et $V$ en $\delta$ "dioptrie", donc $\delta=m^{-1}$).
**Divergente** = **concave ** = lentille **negative**

Fig. 2. Lentilles divergentes.
* Caractérisée par :
\- **Distance focale** (en général en cm) toujours >0 *+* adjectif "**divergente**"
or
\- Sa **distance focale image** $f'$ (en *valeur algébrique*, en général en cm), qui est *négative $f'<0$*.
or
\- Sa **vergence** $V$ (en ophtalmologie) qui est *négative $V<0$*,
avec $V (\delta)=\dfrac{1}{f'(m)}$ ($f'$ étant exprimée en m "mètre" et $V$ en $\delta$ "dioptrie", donc $\delta=m^{-1}$).
### Modélisation analytique
(pour les lentilles minces plongées dans l'air, un gaz ou le vide) for thin lens surrounded by air, gaz or vaccum)
##### relation de conjugaison de le lentille mince
**$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=V=-\dfrac{1}{\overline{OF}}=\dfrac{1}{\overline{OF'}}$**
##### Expression du grandissement transversal
**$M_{T-thinlens}=\dfrac{\overline{OA'}}{\overline{OA}}$**
### Modélisation graphique
#### Représentation d'une lentille mince
* **axe optique** = *axe de révolution* de la lentille, *orienté* positivement en direction de propagation de la lumière (de l'object vers la lentille).
* **Représentation d'une lentille mince** :
\- *sègment de droite*, perpendiculaire à l'axe optique, centré sur l'axe avec *indication symbolique de la forme de la lentille* à ses extrémités (convexe ou concave).
\- **S = C = O** : sommet S = point nodal C (= centre O d'une lentille mince symétrique) $\Longrightarrow$ est utilisé le point O.
\- *point O*, intersection du sègment de droite avec l'axe optique.
\- *point focal objet F* et *point focal image F'*, positionnés sur l'axe optique à égales distances de part et d'autre du point O ($f=-f'$) aux distances algébriques $\overline{OF}=f$ et $\overline{OF'}=f'$.
\- *plan focal objet (P)* et *plan focal image (P')*, plans perpendiculaires à l'axe optique, respectivement aux points $F$ et $F'$.
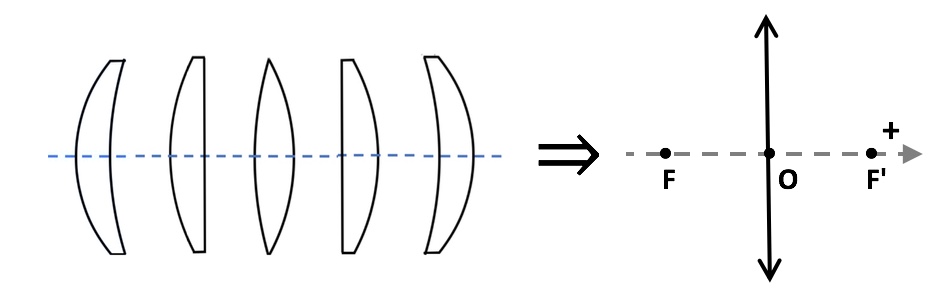
Fig. 3. Représentation d'une lentille mince convergente : $\overline{OF}<0$ , $\overline{OF'}>0$ et $|\overline{OF}|=|\overline{OF'}|$.
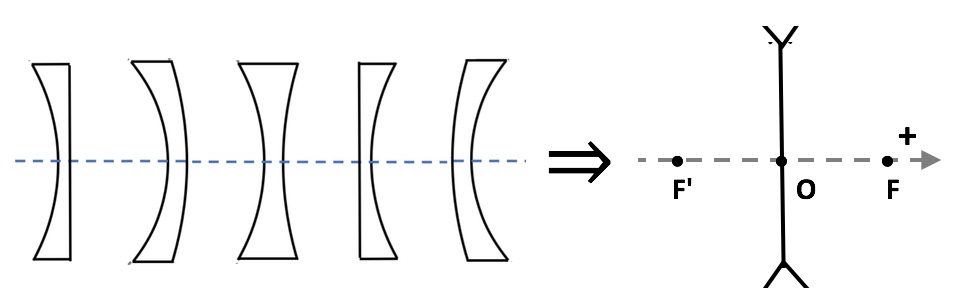
Fig. 3. Représentation d'une lentille mince divergente : $\overline{OF}>0$ , $\overline{OF'}<0$ et $|\overline{OF}|=|\overline{OF'}|$.
#### Détermination des points conjugués :
##### Lentille mince convergente
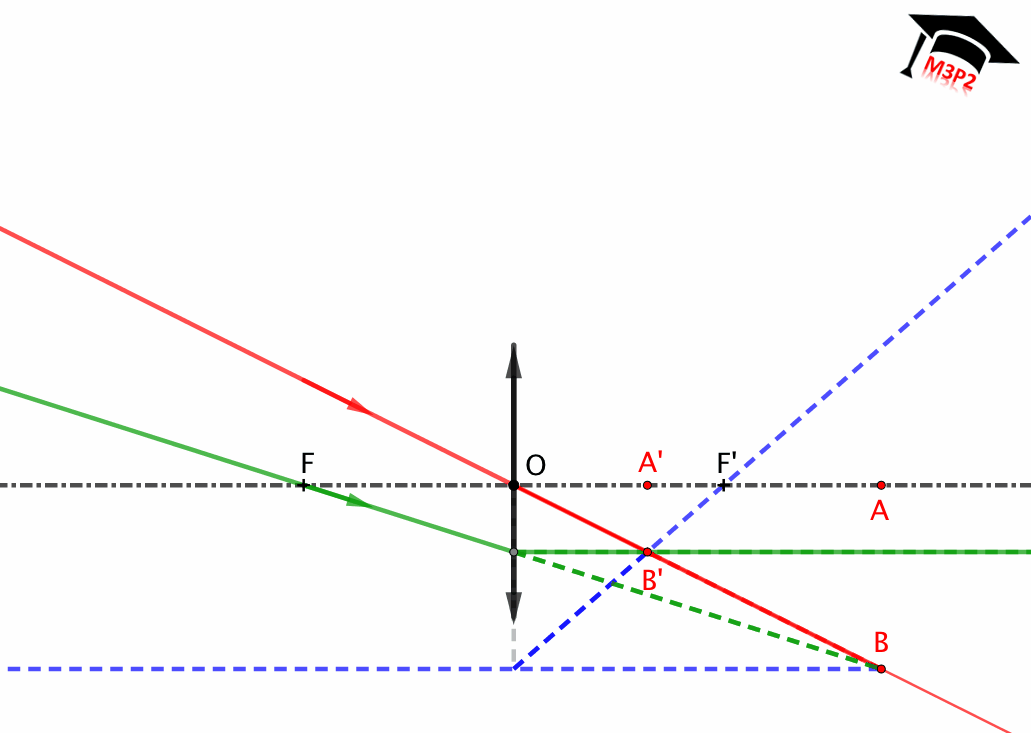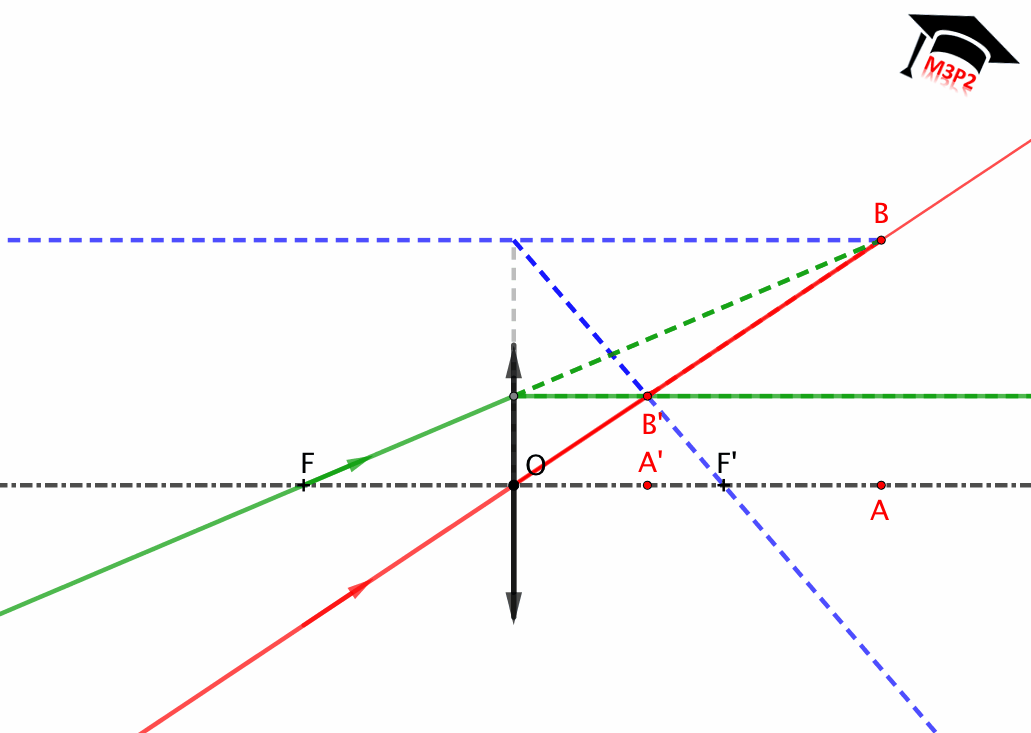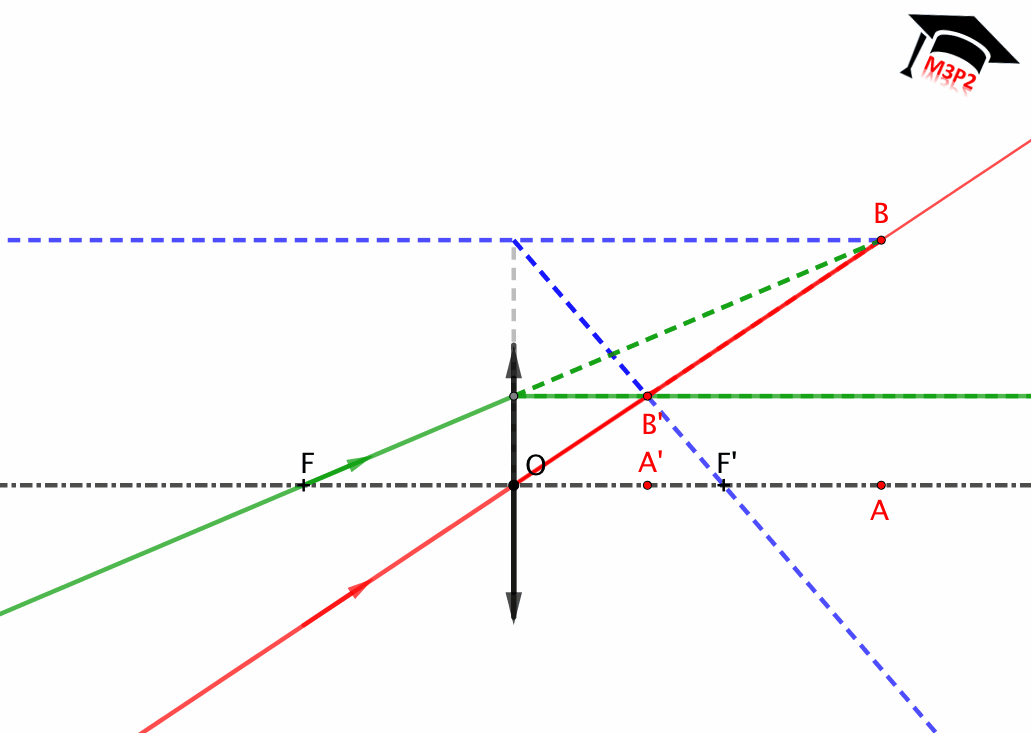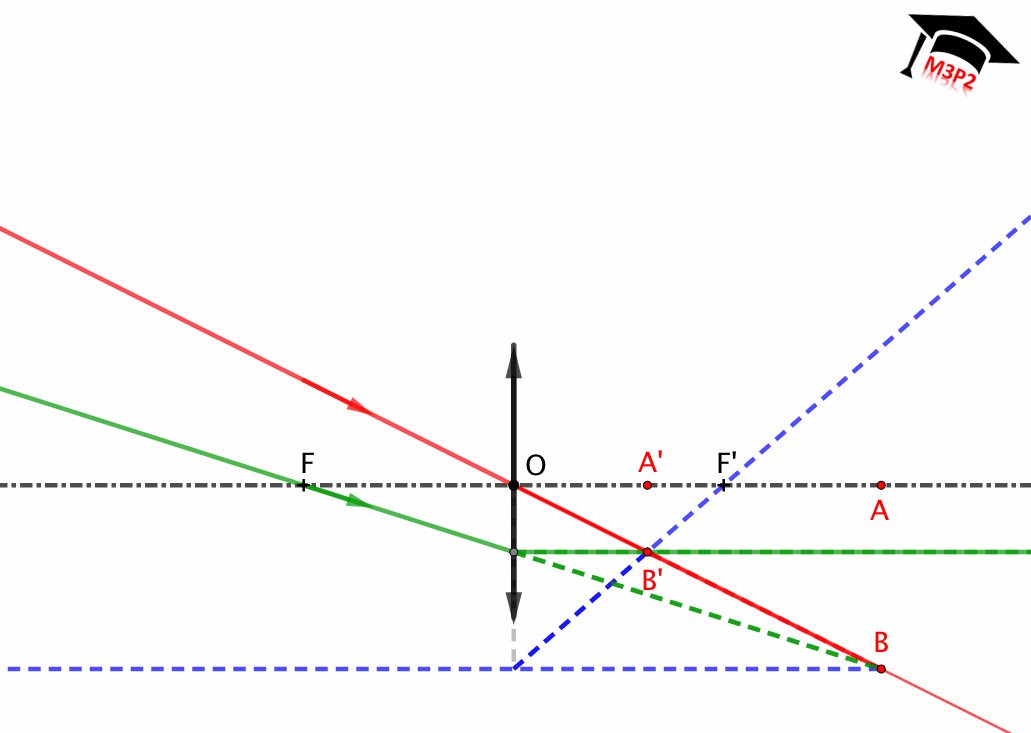
* **Source ponctuelle localisée entre ∞ et F**

* **Source ponctuelle localisée entre F et O**

* **Point object virtuel** (sera expliqué au niveau contreforts).
##### Lentille mince divergente
(à construire)