---
title: Démonstration du théorème de Gauss
published: true
routable: true
visible: false
lessons:
- slug: gauss-ampere-theorems-demonstration
order: 2
---
$`\def\oiint{\displaystyle\mathop{{\iint}\mkern-18mu \scriptsize \bigcirc}}`$
$`\def\Ltau{\Large{\tau}\normalsize}`$
$`\def\Sopen{\mathscr{S}_{\smile}}`$
$`\def\Sclosed{\mathscr{S}_{\displaystyle\tiny\bigcirc}}`$
$`\def\Ssclosed{\mathscr{S}_{\scriptsize\bigcirc}}`$
$`\def\PSopen{\mathscr{S}_{\smile}}`$
$`\def\PSclosed{\mathscr{S}_{\displaystyle\tiny\bigcirc}}`$
!!!! *COURS EN CONSTRUCTION :*
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est *en construction*, il n'est *pas validé par l'équipe pédagogique* à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.
! *Thème* :
! *Electrostatique / Démonstration du théorème de Gauss, forme intégrale et forme locale*
! Guide pour établir les 3 parties : main, overview, beyond
!
! (_précède le thème : Electrostatique : Application du théorème de Gauss, forme intégrale et forme locale._)
ÉNONCÉS DU THÉORÈME DE GAUSS
( appliqué à l' ÉLECTROSTATIQUE )
: ---
*Domaine de validité* :
Électrostatique et Électromagnétisme.
_Attention : Les expressions ci-dessous ne sont valables que dans le système international d'unité $`SI`$, anciennement $`MKS`$._
---
*FORME INTÉGRALE*
La flux du vecteur champ électrique $`\overrightarrow{E}`$ à travers toute surface fermée $`S`$ est égal à la charge électrique totale $`Q_{int}`$ (en valeur algébrique) située à l'intérieur de $`S`$ , divisée par la constante électrique $`\epsilon_0`$ :
$`\displaystyle\mathbf{\oiint_{S} \overrightarrow{E}\cdot\overrightarrow{dS}=\dfrac{Q_{int}}{\epsilon_0}}`$
*Différentes formulations de la charge intérieure* :
* charges discrètes $`q_i`$ : $`Q_{int}=\sum_i q_i`$
* densité volumique de charge $`\rho`$ : $`\displaystyle Q_{int}=\iiint_{\tau\leftrightarrow S} \rho\cdot d\tau`$
avec $`\tau`$ le volume délimité par $`S`$.
*FORME LOCALE*
En tout point de l'espace, la divergence du champ électrique, $`div\,\overrightarrow{E}`$, est égale à la densité volumique de charge en ce point $`\rho`$ divisée par la constante électrique $`\epsilon_0`$ :
$`\mathbf{div\,\overrightarrow{E}=\dfrac{\rho}{\epsilon_0}}`$
---
*avec les unités $`SI`$* :
\- champ électrique $`E`$ : $`V\;m^{-1}`$
\- charge électrique $`Q_{int},q_i`$ : $` C`$
\- densité volumique de charge $`\rho`$ : $` C\;m^{-3}`$
\- $`\epsilon_0=8,85418782\cdot 10^{-12}\;SI`$
#### Quel est l'intérêt du théorème de Gauss intégral ?
* Le théorème de Gauss est un théorème très général.
* Il *permet d'établir l'équation de conservation* de toute grandeur physique.
* Dans la limite où une surface de Gauss tend vers 0, il *permet de définir la notion de divergence* qui quantifie une propriété locale de tout champ vectoriel :
$`\Longrightarrow`$ le théorème de Gauss aura une expression locale.
* Cette notion de divergence est l'*une des trois notions essentielles* (avec le gradient et le rotationnel) *pour décrire les lois de la physique* au niveau universitaire.
* Il *permet de calculer les champs électrostatique $`\overrightarrow{E}`$ et gravitationnel $`\mathcal{\overrightarrow{G}}`$* lorsque les distributions de charge et de masse présentent des invariances et symétries, en remplaçant des calculs qui seraient extrêmement complexes.
#### Quels sont les concepts nécessaires pour comprendre le théorème de Gauss ?
* **Théorème** = *peut être démontré*.
* La démonstration nécessite de connaître les concepts de :
\- *angle solide*.
\- *surface ouverte et surface fermée*.
\- *flux* à travers une surface.
\- *force centrale décroissante en $`1/r^2`$*.
\- *théorème de superposition*.
\- *divergence* d'un champ vectoriel.
#### Qu'est-ce qu'un angle solide ?
##### Que représente-t-il ?
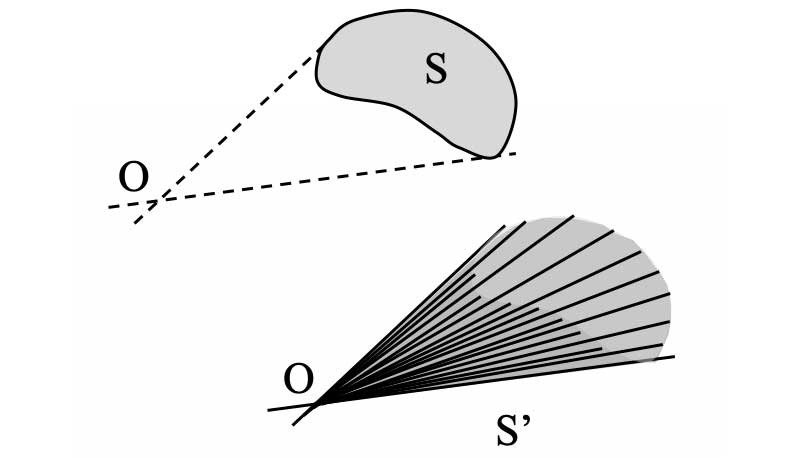
* L’**angle solide** est une notion qui permet de définir et quantifier la *portion d’espace*
\- sous laquelle un observateur voit depuis un point O une surface S dans cet espace.
\- *contenue à l’intérieur d’un faisceau de demi-droites* d'origine $`O`$.
---
##### Comment le définir ?
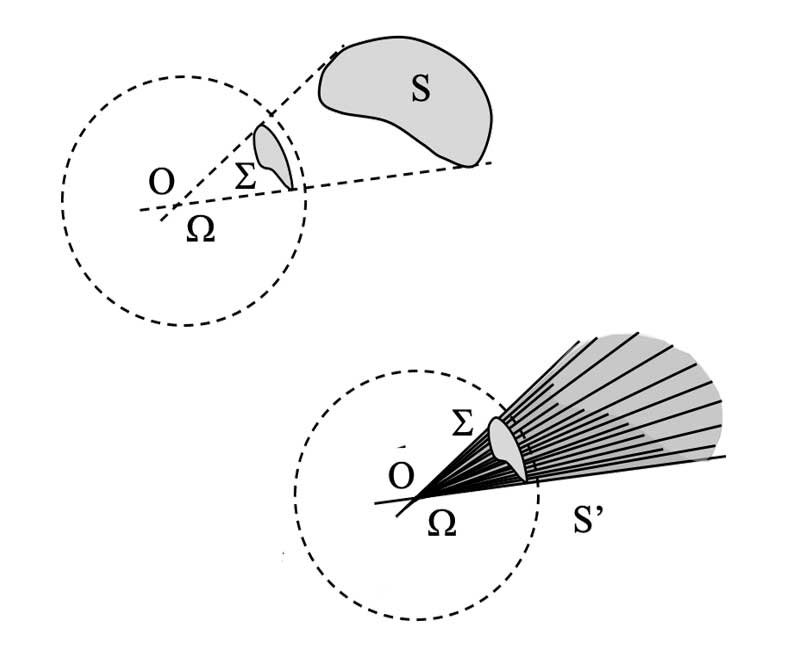
* L’angle solide $`\Omega`$ est défini comme la surface $`\Sigma`$ obtenue par projection de la surface $`S`$ sur la sphère de centre $`O`$ et de rayon $`R`$, divisé par le rayon $`R`$ élevé au carré.
**$`\mathbf{\Omega=\dfrac{\Sigma}{R^2}}`$**
* Ainsi exprimé, l’angle solide est une *grandeur physique sans dimension*. La valeur numérique de l’angle solide ainsi obtenue est l’angle solide exprimé en *stéradian (sr)*.
---
##### Comment le calculer en pratique ?
*Angle solide élémentaire $`d\Omega`$*
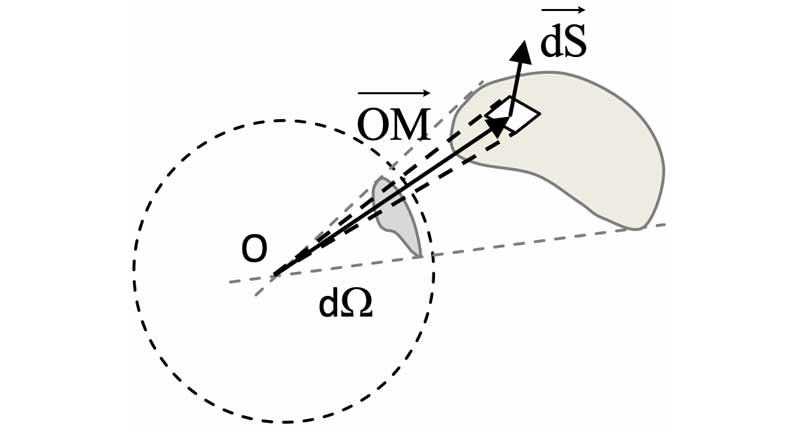
* Si le point $`O`$ et une surface élémentaire orientée $`\overrightarrow{dS}`$ de l’espace sont donnés, alors :
**$`\displaystyle\mathbf{d\Omega=\dfrac{|\,\overrightarrow{OM}\cdot\overrightarrow{dS}\,|}{OM^3}}\quad`$**,
avec $`OM=||\overrightarrow{OM}||`$
* **En notation algébrique**, l'angle solide élémentaire peut être positif ou négatif :
**$`\displaystyle\mathbf{d\Omega=\dfrac{\overrightarrow{OM}\cdot\overrightarrow{dS}}{OM^3}}\quad`$**,
avec $`OM=||\overrightarrow{OM}||`$
Lorsque la surface est ouverte, deux sens sont possibles pour l’orientation des $`\overrightarrow{dS}`$, qui conditionnent le signe de l’angle solide.
---
*Angle solide $`\Omega`$*
* Si le point $`O`$ et une surface orientée $`S`$ de l’espace sont donnés, alors :
**$`\displaystyle\mathbf{\Omega=\iint d\Omega=\iint_S \dfrac{|\,\overrightarrow{OM}\cdot\overrightarrow{dS}\,|}{OM^3}}\quad`$**,
avec $`OM=||\overrightarrow{OM}||`$
* **En notation algébrique**, l'angle solide peut être positif ou négatif :
**$`\displaystyle\mathbf{\Omega=\iint d\Omega=\iint_S \dfrac{\overrightarrow{OM}\cdot\overrightarrow{dS}}{OM^3}}\quad`$**,
avec $`OM=||\overrightarrow{OM}||`$
#### Qu'est-ce qu'une surface ouverte ou fermée ?
* **surface fermée** : *frontière délimitant un volume intérieur et un espace extérieur*.
$`\Longrightarrow`$ par convention :
\- les éléments vectoriels de surface **$`\overrightarrow{dS}`$** sont **orientés de l'intérieur vers l'extérieur**.
\- l'*intégration* sur une surface fermée utilise le **symbole $`\oiint_S...\,dS`$**
* **surface ouverte** : *n'est pas la frontière d'un volume*.
$`\Longrightarrow`$ :
\- l'*orientation* des éléments vectoriels de surface **$`\overrightarrow{dS}`$** doit être choisie parmi les **deux sens possibles**.
\- l'*intégration* sur une surface fermée utilise le symbole **$`\displaystyle\iint_S...\,dS`$**.
#### Qu'est-ce que le flux d'un champ vectoriel à travers une surface ?
##### Flux élémentaire d'un champ vectoriel
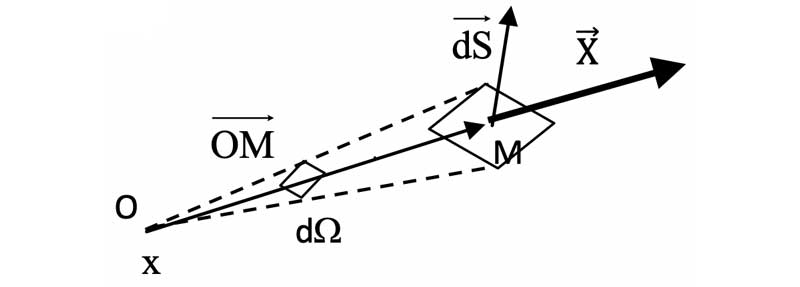
* Le **flux élémentaire $`d\Phi_X`$** d'un champ vectoriel $`\overrightarrow{X}`$ est le flux de $`\overrightarrow{X}`$ à travers un élément vectoriel de surface $`\overrightarrow{dS}`$.
* Par définition, $`d\Phi_X`$ est le *produit scalaire $`\overrightarrow{X}\cdot\overrightarrow{dS}`$* :
**$`\mathbf{d\Phi_X=\overrightarrow{X}\cdot\overrightarrow{dS}}`$**
---
##### Flux d'un champ vectoriel à travers une surface
* $`\displaystyle\Phi_X=\int d\Phi_X`$
* flux à travers une *surface ouverte* : **$`\displaystyle\mathbf{\Phi_X=\iint_S \overrightarrow{X}\cdot\overrightarrow{dS}}`$**.
* flux à travers une *surface fermée* : **$`\displaystyle\mathbf{\Phi_X=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}}`$**.
#### Qu'est-ce qu'un champ de force centrale décroissante en $`1/r^2`$ ?
* **Force centrale** : force d'interaction à distance, toujours *dirigée en direction de sa source élémentaire*.
(élémentaire = considérée comme °ponctuelle* à l'échellle d'observation).
* **Force décroissante en $`1/r^2`$** : force d'interaction à distance, dont *l'intensité décroit comme le carré de la distance* à sa source ponctuelle.
* **Expression générale** *d'un champ de force centrale décroissante en $`1/r^2`$* :
**$`\mathbf{\overrightarrow{X}=K\cdot x\cdot\dfrac{\overrightarrow{OM}}{OM^3}}\quad`$**, avec :
\- $`O`$ : point où se situe la source élémentaire.
\- $`x`$ : grandeur physique qui caractérise la sensibilité de la source élémentaire à l'interaction X.
\- $`M`$ : point où est exprimé le champ de la force.
\- $`K`$ : constante réelle qui dépend du système d'unités.
\- $`OM=||\overrightarrow{OM}||`$.
et *dans le repère sphérique $`(O,\overrightarrow{e_r},\overrightarrow{e_{\theta}},\overrightarrow{e_{\varphi}})`$* :
**$`\mathbf{\overrightarrow{X}=K\cdot\dfrac{x}{r^2}\cdot\overrightarrow{e_r}}\quad`$**
avec $`r=OM\quad`$ et $`\quad\overrightarrow{e_r}=\dfrac{\overrightarrow{OM}}{OM}`$.
!!! Exemples de champs de force centrale décroissantes en $`1/r^2`$ :
!!! \- champ gravitationnel : $`\mathcal{\overrightarrow{G}}=-\,G\cdot\dfrac{m}{r^2}\cdot\overrightarrow{e_r}`$.
!!! \- champ électrostatique : $`\overrightarrow{E}=\dfrac{1}{4\pi\varepsilon_0}\;\dfrac{q}{r^2}\cdot\overrightarrow{e_r}`$.
!!!
!!!
!!! Plus d'information sur ces deux expressions
!!!
!!! Sont données en coordonnées sphériques :
!!! \-expression du champ gravitationnel créé à une distance $`r`$ d'une source élémentaire de masse $`m`$ située en !!! $`O`$, G est la constante universelle de gravitation.
!!! \-expression du champ électrique créé à une distance $`r`$ d'une source élémentaire de charge électrique $`q`$ immobile en $`O`$, $`\varepsilon_0`$ est la permittivité électrique du vide, encore appelée constante électrique.
!!!
#### Quelle propriété particulière possède le flux d'un champ de force centrale décroissante en $`1/r^2`$ ?
Flux d'un champ de force centrale en $`1/r^2`$ à travers une surface fermée
##### Expression du flux élémentaire
* $`d\Phi_X=\overrightarrow{X}\cdot\overrightarrow{dS}`$
$`\quad=\left(K\cdot x\cdot\dfrac{\overrightarrow{OM}}{OM^3}\right)\cdot\overrightarrow{dS}`$
$`\quad=K\cdot x\cdot\left(\dfrac{\overrightarrow{OM}\cdot\overrightarrow{dS}}{OM^3}\right)`$
**$`\mathbf{d\Phi_X=K\cdot x\cdot d\Omega}`$**
##### La surface fermée ne contient pas la source ponctuelle du champ
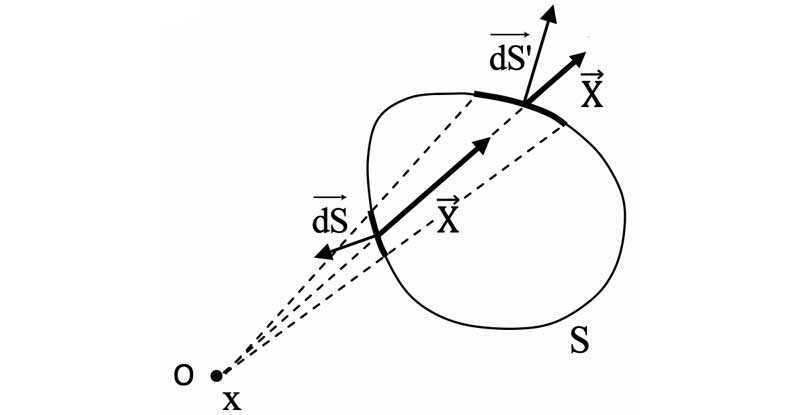
* Partant de $`O`$, toute demi-droite $`\Delta`$ en direction de la surface $`S`$ traverse $`S`$ un nombre pair de fois .
* Observé dans un même angle solide $`d\Omega`$ centré autour de $`\Delta`$, le flux élémentaire total
$`d\Phi_{\Delta}`$ est égal à la somme d'un nombre pair $`2n`$ de flux élémentaires $`d\Phi_i`$ d'égales valeurs absolues.
* Dans une moitié des cas : $`0<\widehat{\overrightarrow{X}\overrightarrow{dS}}<\pi/2 \Longrightarrow d\Phi_i>0`$,
dans l'autre moitié : $`\pi/2<\widehat{\overrightarrow{X}\overrightarrow{dS}}<\pi \Longrightarrow d\Phi_i<0`$
$`\Longrightarrow`$*$`\;d\Phi_{\Delta}=\sum d\Phi_i=0`$*.
* *$`\Longrightarrow`$ Le flux $`\Phi_X`$ à travers toute surface fermée qui ne contient pas la source de $`X`$ est nul* :
**$`\mathbf{\Phi_X=\displaystyle\int_S d\Phi_{\Delta} =\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}=0}`$**
---
##### La surface fermée contient la source ponctuelle du champ
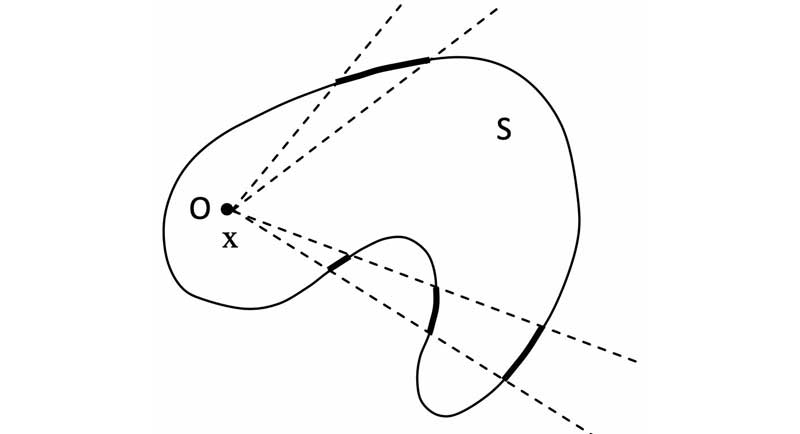
* Partant de $`O`$, toute demi-droite $`\Delta`$ en direction de la surface $`S`$ traverse $`S`$ un nombre impair de fois .
* Observé dans un même angle solide $`d\Omega`$ centré autour de $`\Delta`$, le flux élémentaire total
$`d\Phi_{\Delta}`$ est égal à la somme d'un nombre impair $`2n+1`$ de flux élémentaires $`d\Phi_i`$ d'égales valeurs absolues.
* $`2n`$ flux élémentaires s'annulent, et le flux élémentaire total $`d\Phi_{\Delta}`$ est égal au flux restant :
$`\Longrightarrow`$**$`\; d\Phi_{\Delta}=\sum d\Phi_i=K\cdot x\cdot d\Omega\quad`$**,
avec $`d\Phi_{\Delta}>0\;\Longleftrightarrow\;x>0`$.
* Le flux $`\Phi_X`$ à travers toute surface fermée qui contient la source de $`X`$ est égal à :
$`\Phi_X=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}=\int_{\Omega_S} K\cdot x\cdot d\Omega`$
* Depuis le point $`O`$ situé à l'intérieur de la surface fermée $`S`$, l'angle solide $`\Omega_S`$ sous lequel est vue $`S`$ est de $`4\pi`$ stéradians : $`\Omega_S=2\pi\;\text{sr}`$
* *$`\Longrightarrow`$ Le flux $`\Phi_X`$ à travers toute surface fermée qui contient pas la source de $`X`$ est nul* :
**$`\mathbf{\Phi_X=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}=4\pi\,K\,x}`$**
---
#### Qu'est-ce que le théorème de superposition ?
* La présence ou non d'autre sources n'influence pas le champ $`\overrightarrow{X}_{tot}`$ créé par une source élémentaire. Donc le champ total $` X`$ créé par une distribution de sources élémentaires est la somme des champs $`X`$ créé par chacune des sources élémentaires.
* $`\Longrightarrow`$ :
\- pour une *distribution discrète de sources* : **$`\mathbf{\overrightarrow{X}_{tot}=\sum_i \overrightarrow{X}_i}`$**.
\- pour une *distribution continue de sources* : **$`\displaystyle\mathbf{\overrightarrow{X}_{tot}=\int d\overrightarrow{X}}`$**.
#### Que devient le flux à travers une surface fermée contenant plusieurs sources de champ ?
* Soit **$`S`$** une **surface fermée** dans l'espace démilitant un *volume $`\tau`$*.
* Si $`S`$ contient en un point $`P_1`$ une **unique source $`x_1`$** créant une champ vectoriel $`\overrightarrow{X_1}`$ central décroissant en $`1/r^2`$, le flux $`\Phi_{X_1}`$ de $`\overrightarrow{X_1}`$ à travers $`S`$ s'écrit :
**$`\mathbf{\Phi_{X_1}=\oiint_S \overrightarrow{X_1}\cdot\overrightarrow{dS}=4\pi\,K\, x_1}`$**
* Si $`S`$ contient en un autre point $`P_2`$ une **unique autre source $`x_2`$**, de même le flux flux $`\Phi_{X_2}`$ s'écrit :
**$`\mathbf{\Phi_{X_2}=\oiint_S \overrightarrow{X_1}\cdot\overrightarrow{dS}=4\pi\,K\, x_2}`$**
* Si les sources **$`x_1`$ et $`x_2`$ existent simultanément**, alors le *théorème de superposition* dit qu'en tout point de l'espace, le champ électrostatique total $`\overrightarrow{X}`$ est la somme des champs $`\overrightarrow{X_1}`$ et $`\overrightarrow{X_2}`$ :
*$`\overrightarrow{X}=\overrightarrow{X_1}+\overrightarrow{X_2}`$*
$`\Longrightarrow`$ le flux total de $`\overrightarrow{X}`$ à travers $`S`$ s'écrit :
$`\Phi_{X}=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}`$
$`\quad=\oiint_S (\overrightarrow{X_1}+\overrightarrow{X_2})\cdot\overrightarrow{dS}`$
$`\quad=\oiint_S \overrightarrow{X_1}\cdot\overrightarrow{dS}+\oiint_S \overrightarrow{X_2}\cdot\overrightarrow{dS}`$
**$`\mathbf{\Phi_{X}=4\pi\,K\,(x_1+x_2)}`$**
* Ce résultat *se généralise facilement* à tout nombre entier de sources discrètes $`x_i`$ ou à une distribution continue de densité volumique $`\rho_x(\overrightarrow{r})`$
\- pour *n sources discrètes* :
**$`\displaystyle\mathbf{\quad\Phi_{X}=4\pi\,K\,\sum_{i=1}^n s_i}`$**
\- pour une *densité volumique $`\mathbf{\rho_x(\overrightarrow{r})}`$* :
**$`\displaystyle\mathbf{\quad\Phi_{X}=4\pi\,K\,\iiint_{\Ltau} \rho_x(\overrightarrow{r})\cdot d\tau}`$**
#### Que dit le théorème de Gauss intégral en électrostatique ?
##### L'interaction électrostatique
* La **charge électrique**, de symbole **$`q`$**, est la grandeur physique $`x`$ qui *caractérise la sensibilté d'un corps à l'interaction électrostatique* (et plus généralement à l'interaction électromagnétique).
* La charge $`q`$ peut être **négative ou positive**.
* La **force d'interaction électrostatique** $`\overrightarrow{F}_{1\rightarrow 2}`$ qu'exerce une particule de charge $`q_1`$ immobile en $`M_1`$ sur une autre particule de charge $`q_2`$ située en $`M_2`$ s'écrit :
**$`\mathbf{\overrightarrow{F}_{1\rightarrow 2}=\dfrac{1}{4\pi\,\epsilon_0}\cdot q_1\,q_2\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}}`$**
C'est une *force centrale décroissant en $`1/r^2`$*$`\quad\Longrightarrow`$ le théorème de Gauss s'applique.
* Cette force se réécrit :
$`\overrightarrow{F}_{1\rightarrow 2}=q_2\cdot \overrightarrow{E_{1,M_2}}`$
où $`\overrightarrow{E_{1,M_2}}`$ est le champ électrostatique créé par la particule immobile en $`M_1`$ au point $`M_2`$ :
$`\overrightarrow{E}_{1\rightarrow 2}=\dfrac{1}{4\pi\,\epsilon_0}\cdot q_1\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}`$
C'est une force centrale décroissant en $`1/r^2`$.
* Le **champ électrostatique** créé en tout point $`M`$ de l'espace par une particule de charge $`q`$ immobile en un point $`O`$ s'écrit :
**$`\mathbf{\overrightarrow{E}=\dfrac{1}{4\pi\,\epsilon_0}\cdot q\cdot \dfrac{\overrightarrow{OM}}{OM^3}}`$**
##### Quel est le lien entre électrostatique et électromagnétisme ?
* L'électrostatique décrit le champ électrique créé par des particules chargées immobile.
* L'électromagnétisme généralise aux champs électrique et magnétiques créés par des particules chargées immobiles ou en mouvement.
##### Le théorème de Gauss intégral en électrostatique
* Soit une *distribution de charges maintenues immobiles* dans l'espace.
* **Théorème de Gauss** :
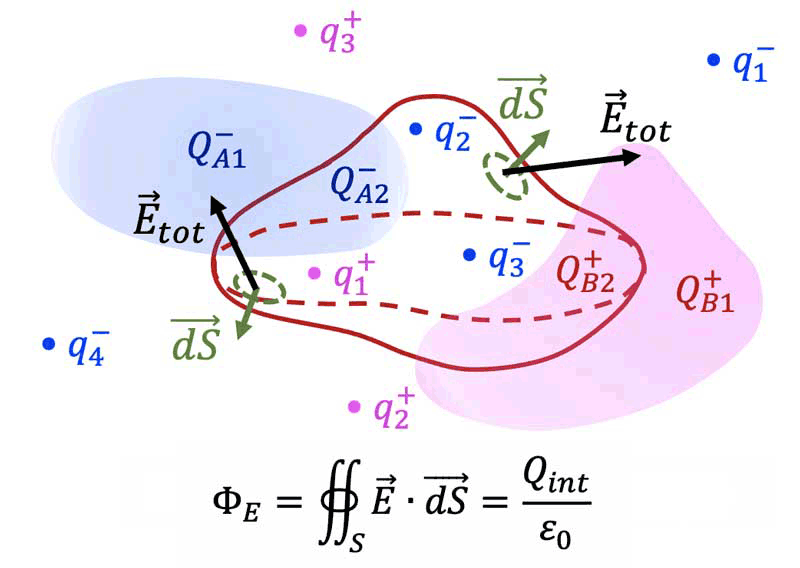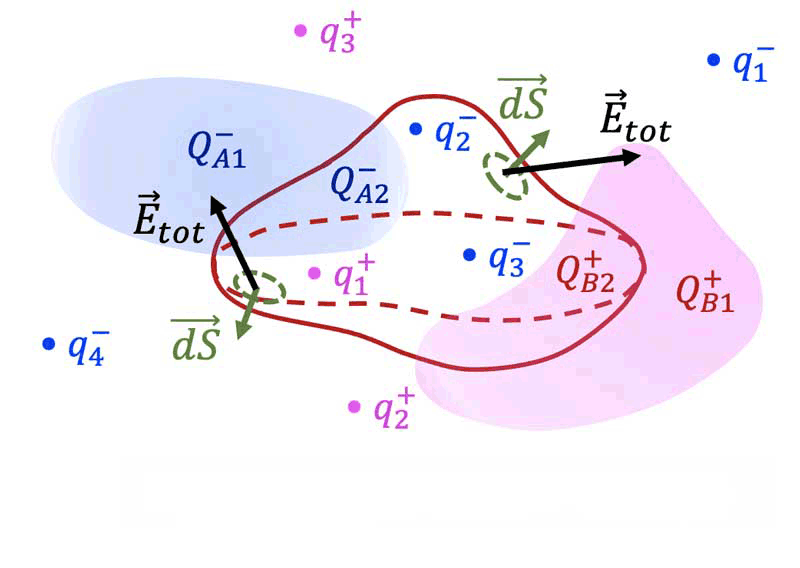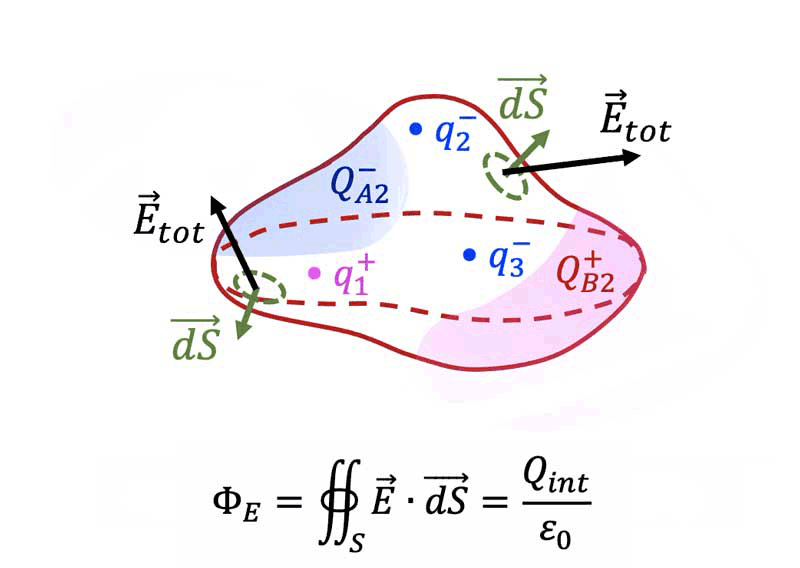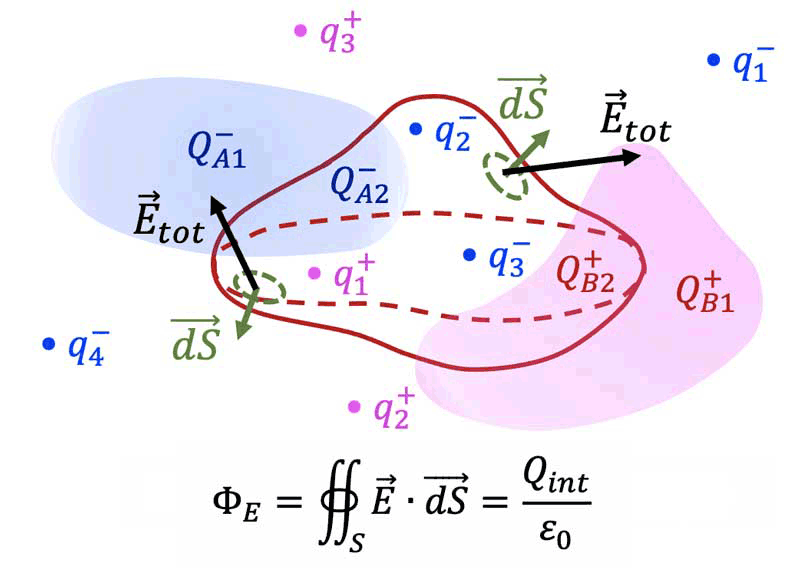
Le flux $`\Phi_E`$ du vecteur champ électrique à travers toute *surface fermée $`S`$* de l'espace
est égal à la *charge totale $`Q_{int}`$ contenue à l'intérieur de $`S`$* divisée par la constante électrique $`\epsilon_0`$.
**$`\mathbf{\Phi_E=\oiint_S \overrightarrow{E}\cdot\overrightarrow{dS}=\dfrac{Q_{int}}{\epsilon_0}}`$**
##### Quelles sont les différentes expression de $`Q_{int}`$ rencontrées?
* Pour *n charges discrètes $`q_i`$* dans le volume $`\tau`$ :
**$`\displaystyle\mathbf{Q_{int}=\sum_{i=1}^n q_i}`$**
* Pour une *densité volumique de charge $`\mathbf{\rho(\overrightarrow{r})}`$* (cas de la réalité 3D à l'échelle d'observation) :
**$`\displaystyle\mathbf{Q_{int}=\iiint_{\Ltau} \rho(\overrightarrow{r}) \cdot d\tau }`$**
* Lorsque les charges sont réparties sur une surface $`S`$ (2D $`\Longleftrightarrow`$ une épaisseur 1D est négligée) avec une *densité surfacique de charge $`\mathbf{\sigma}`$* :
**$`\displaystyle\mathbf{Q_{int}=\iint_{S\cap\Ltau} \sigma(\overrightarrow{r}) \cdot dS }`$**
* Lorsque les charges sont réparties sur un fil $`\Gamma`$ (1D $`\Longleftrightarrow`$ une section 2D est négligée) avec une *densité linéïque de charge $`\mathbf{\lambda}`$* :
**$`\displaystyle\mathbf{Q_{int}=\int_{\Gamma\cap\Ltau} \lambda(\overrightarrow{r}) \cdot dl }`$**
----
#### Que dit le théorème de Gauss intégral en gravitation ?
##### L'interaction gravitationnelle
* La **masse**, de symbole **$`m`$**, est la grandeur physique $`x`$ qui *caractérise la sensibilté d'un corps à l'interaction gravitationnelle*.
* La masse $`m`$ de la matière est *toujours positive*.
* La **force d'interaction gravitationnelle de Newton** $`\overrightarrow{F}_{1\rightarrow 2}`$ qu'exerce un corps de masse $`m_1`$ en $`M_1`$ sur un autre corps de masse $`m_2`$ située en $`M_2`$ s'écrit :
**$`\mathbf{\overrightarrow{F}_{1\rightarrow 2}=-\;G\cdot m_1\,m_2\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}}`$**
où $`G`$ est la constante universelle de la gravitation.
C'est une *force centrale décroissant en $`1/r^2`$*$`\quad\Longrightarrow`$ le théorème de Gauss s'applique.
* Cette force se réécrit :
$`\overrightarrow{F}_{1\rightarrow 2}=m_2\cdot \mathcal{\overrightarrow{G}}_{M_1,M_2}`$
où $`\mathcal{\overrightarrow{G}}_{M_1,M_2}`$ est le champ gravitationnel créé par le corps en $`M_1`$ au point $`M_2`$ :
$`\mathcal{\overrightarrow{G}}_{M_1,M_2}=\;G\cdot m_1\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}`$
C'est une force centrale décroissant en $`1/r^2`$.
* Dans le cadre de la physique classique, le **champ gravitationnel $`\mathcal{\overrightarrow{G}}`$** créé en tout point $`M`$ de l'espace par un corps de masse $'m`$ situé un point $`O`$ s'écrit :
**$`\mathbf{\mathcal{\overrightarrow{G}}=-\;G\cdot m\cdot \dfrac{\overrightarrow{OM}}{OM^3}}`$**
##### Théorème de Gauss intégral en gravitation
* Soit une *distribution de masses* dans l'espace.
* **Théorème de Gauss** :
Le flux $`\Phi_{\mathcal{G}}`$ du vecteur champ de gravitation $`\mathcal{\overrightarrow{G}}`$ à travers toute *surface fermée $`S`$* de l'espace
est égal à la *masse totale $`m_{int}`$ contenue à l'intérieur de $`S`$* multiplié par $`4\pi\,G`$, où $`G`$ est la constante la constante universelle de la gravitation.
**$`\mathbf{\Phi_{\mathcal{G}}=\oiint_S \mathcal{\overrightarrow{G}}\cdot\overrightarrow{dS}=-\,4\pi\,G\,m_{int}}`$**
#### Pourquoi le théorème de Gauss intégral est-il insuffisant ?
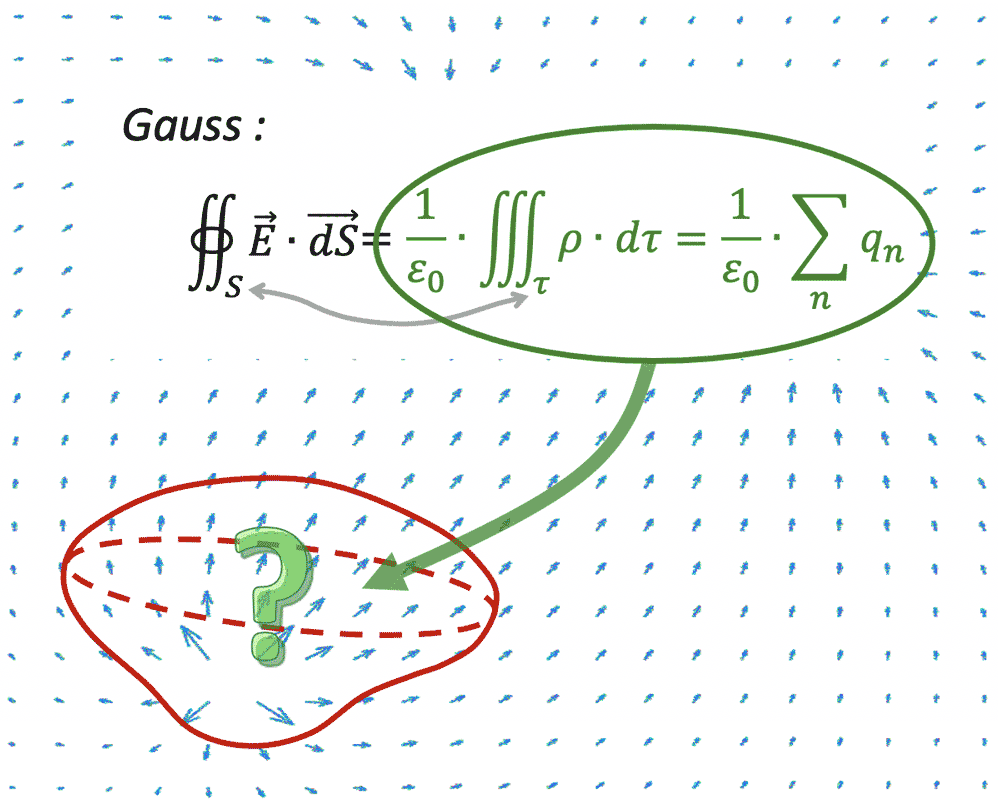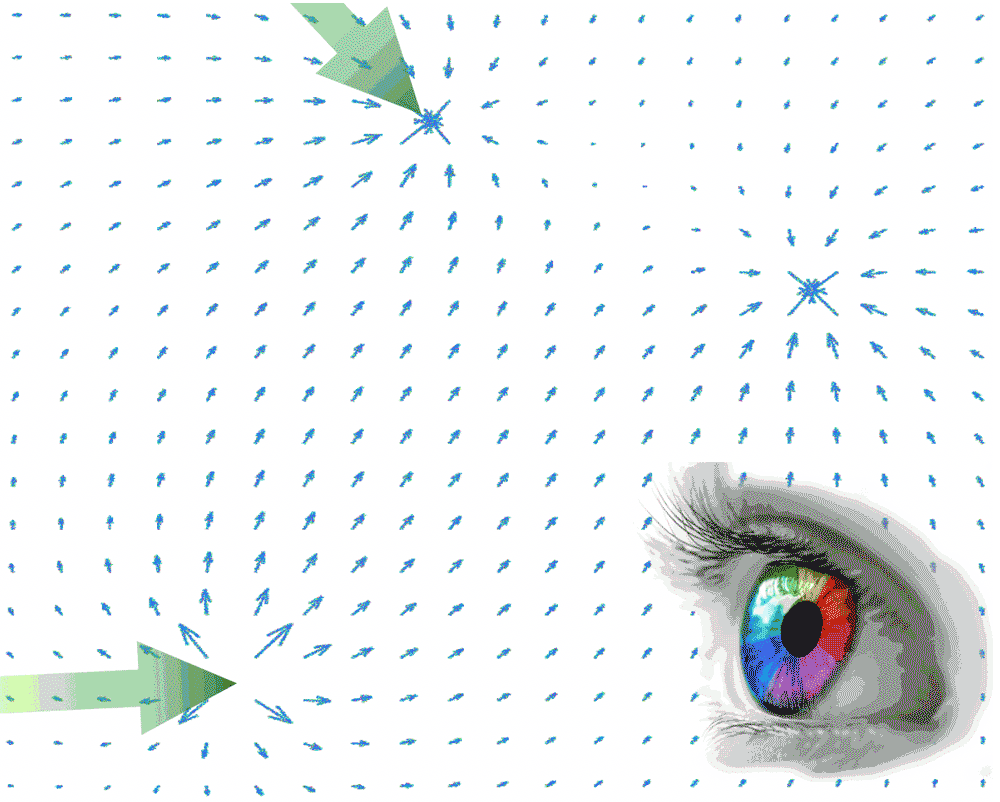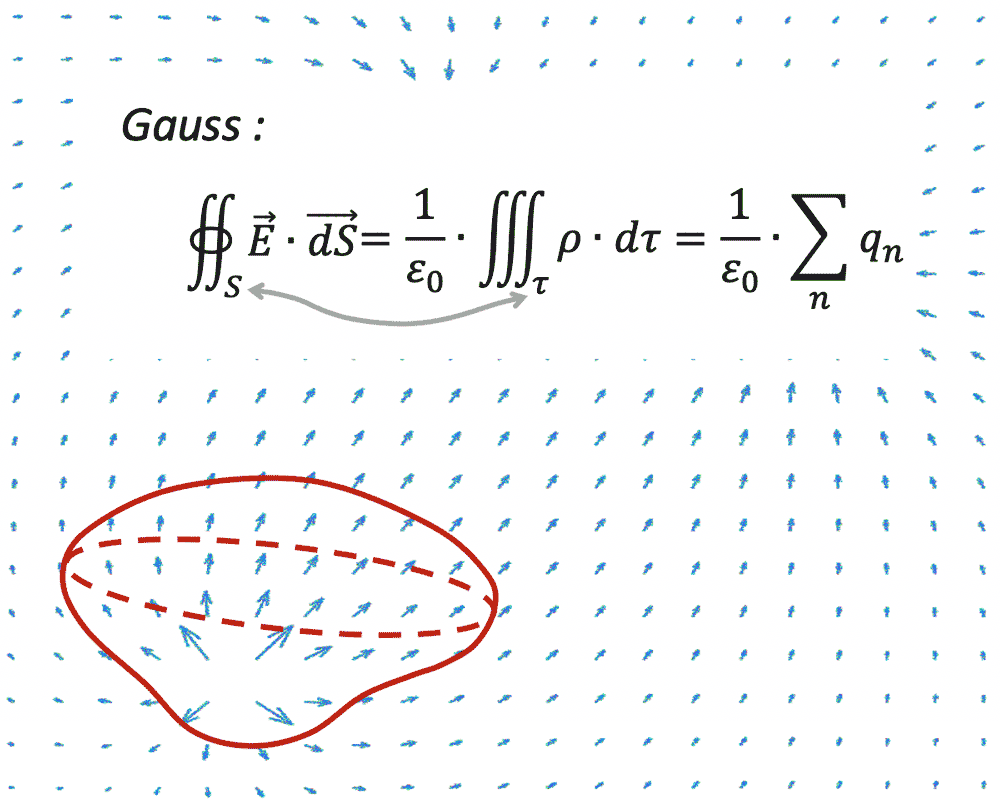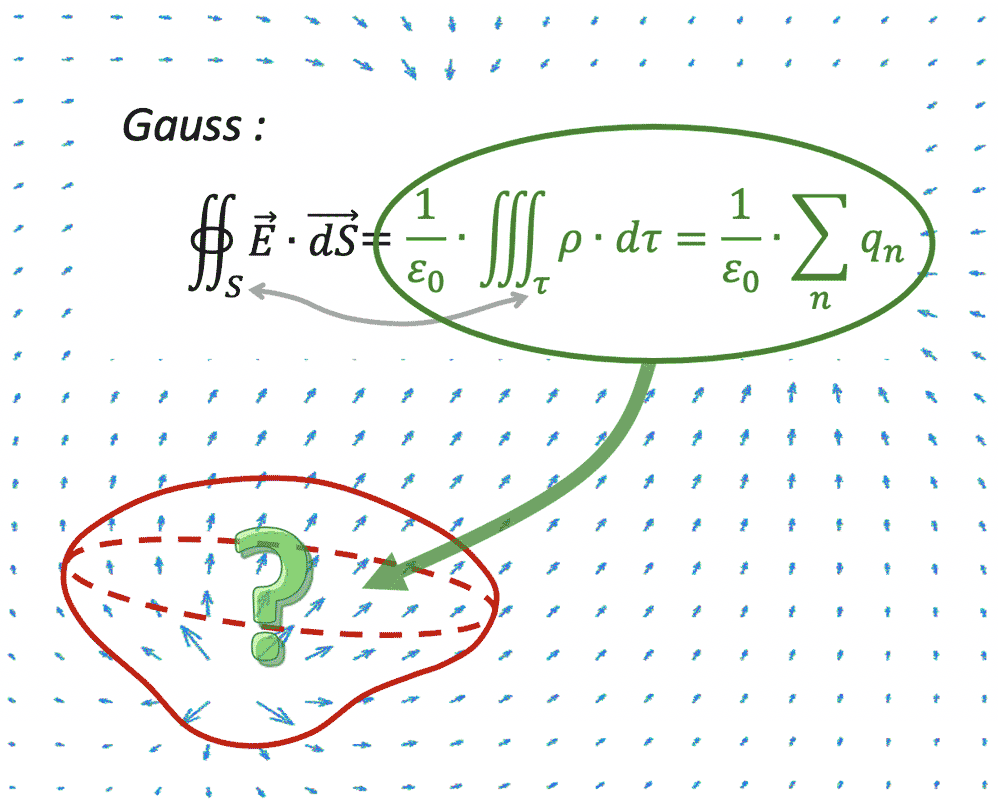
_Champ électrique créé par 3 charges ponctuelles immobiles situées dans plan de représentation du champ
électrostatique._
---
* Dans les *cas simples*, **l'oeil humain repère immédiatement** les points où les lignes de champ électrique convergent ou divergent, qui localisent *les causes du champ électrostatique* dans le plan d'observation.
* Le **théorème de Gauss intégral** précise, lors d'un flux non nul du champ électrostatique
à travers une surface fermée $`S`$, la somme totale des charges contenues dans $`S`$ à l'origine de ce flux,
mais *ne permet pas la localisation précise de ces charges*.
* Il **doit exister une propriété locale** (à l'échelle mésoscopique, donc apparaissant ponctuelle
à la résolution de l'observation) qui en tout point de l'espace *relie le champ électrostatique
à sa cause élémentaire locale*.
#### Une idée pour relier une propriété locale du champ électrostatique à sa cause ?
* Dans la **démonstration du théorème de gauss** (partie principale), *aucune échelle de taille n'est précisée*
pour le choix de la surface fermée de Gauss, et donc du volume intérieur qu'elle définit.
* $`\Longrightarrow`$ idée 1 : faire tendre la surface fermée vers une
**surface fermée mésoscopique qui entoure chaque point** de résolution de l'espace,
le *flux* ainsi calculé sera une *propriété locale du champ*.
* $`\Longrightarrow`$ idée 2 : la *charge déduite du théorème de Gauss* est la charge **située à l'intérieur du volume mésoscopique** délimité par cette surface de Gauss, c'est ainsi une charge *locale*.
* Cette idée est à la **base de la notion de divergence** d'un champ vectoriel.
#### Comment est définie la divergence d'un champ vectoriel X ?
* Soit $`dS`$ un élément de surface fermée qui délimite un élement de volume $`d\tau`$ contenu dans un voisinage de tout point de l'espace.
La **divergence de $`\overrightarrow{X}`$**, *définie en tout point de l'espace*, est le flux $`d\Phi_X`$ de $`\overrightarrow{X}`$ à travers $`dS`$, divisé par le volume $`d\tau`$ :
**$`\mathbf{div\,\overrightarrow{X}=\displaystyle \lim_{\tau\leftrightarrow 0 \\ \tau \leftrightarrow S} \dfrac{\displaystyle\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}}{\displaystyle\iiint_{\tau} d\tau}=\dfrac{d\Phi_X}{d\tau}}`$**
* $`\Longrightarrow`$*$`\mathbf{\quad d\Phi_X=div\,\overrightarrow{X}\cdot d\tau}`$*.
#### Que représente-t-elle ?
La champ de divergence de X est un **champ scalaire** : $`div\;\overrightarrow{X}\in\mathbb{R}`$
* Le **valeur absolue de la divergence $`\mathbf{|\,div\;\overrightarrow{X}\,|}`$** indique l'*intensité du champ $`\overrightarrow{X}`$* ce point.
( $`div\;\overrightarrow{X}=0`$ indique un champ qui ne converge ni ne diverge en ce point)
* Le **signe de $`\mathbf{div\;\overrightarrow{X}}`$** indique si la *vergence du champ $`\mathbf{\overrightarrow{X}}`$* en ce point.
\- **$`\mathbf{div\;\overrightarrow{X}<0}`$**$`\quad\Longleftrightarrow\quad`$ le champ *$`\mathbf{\overrightarrow{X}}`$ diverge*.
\- **$`\mathbf{div\;\overrightarrow{X}>0}`$**$`\quad\Longleftrightarrow\quad`$ le champ *$`\mathbf{\overrightarrow{X}}`$ converge*.
#### Comment se détermine son expression en coordonnées cartésiennes ?
* Soit un **élément de volume $`d\tau=dx\,dy\,dz`$** centré en tout point $`M`$ de l'espace.
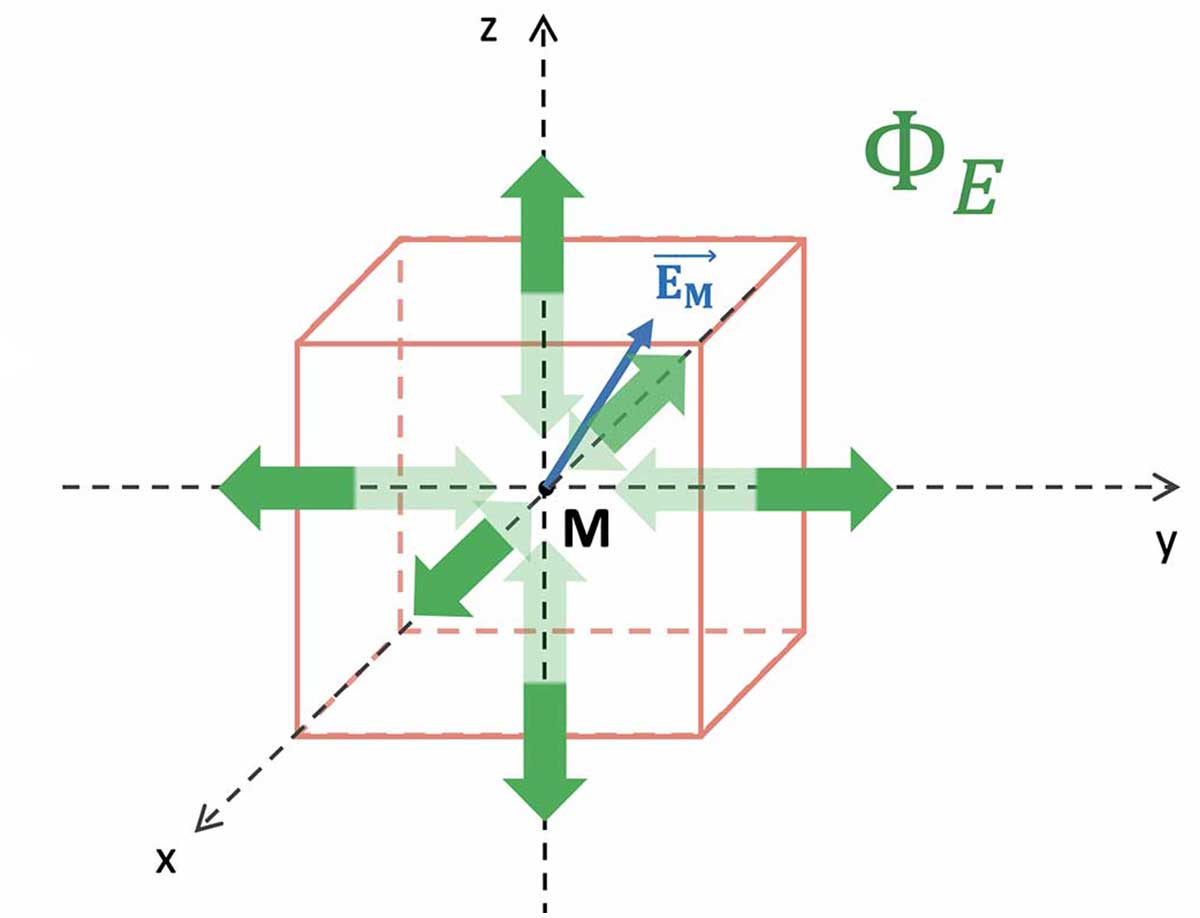
---
* Soit **$`\overrightarrow{X_M}`$** le **champ vectoriel au point $`M`$** dû à l'ensemble de ses sources dans l'espace.
* Le **flux $`\Phi_X`$** de *$`\overrightarrow{X}`$ à travers la surface fermée $`dS`$* délimitant $`d\tau`$ est la somme des flux de $`\overrightarrow{X}`$ à travers chacune des six faces élémentaires constituant $`dS`$.
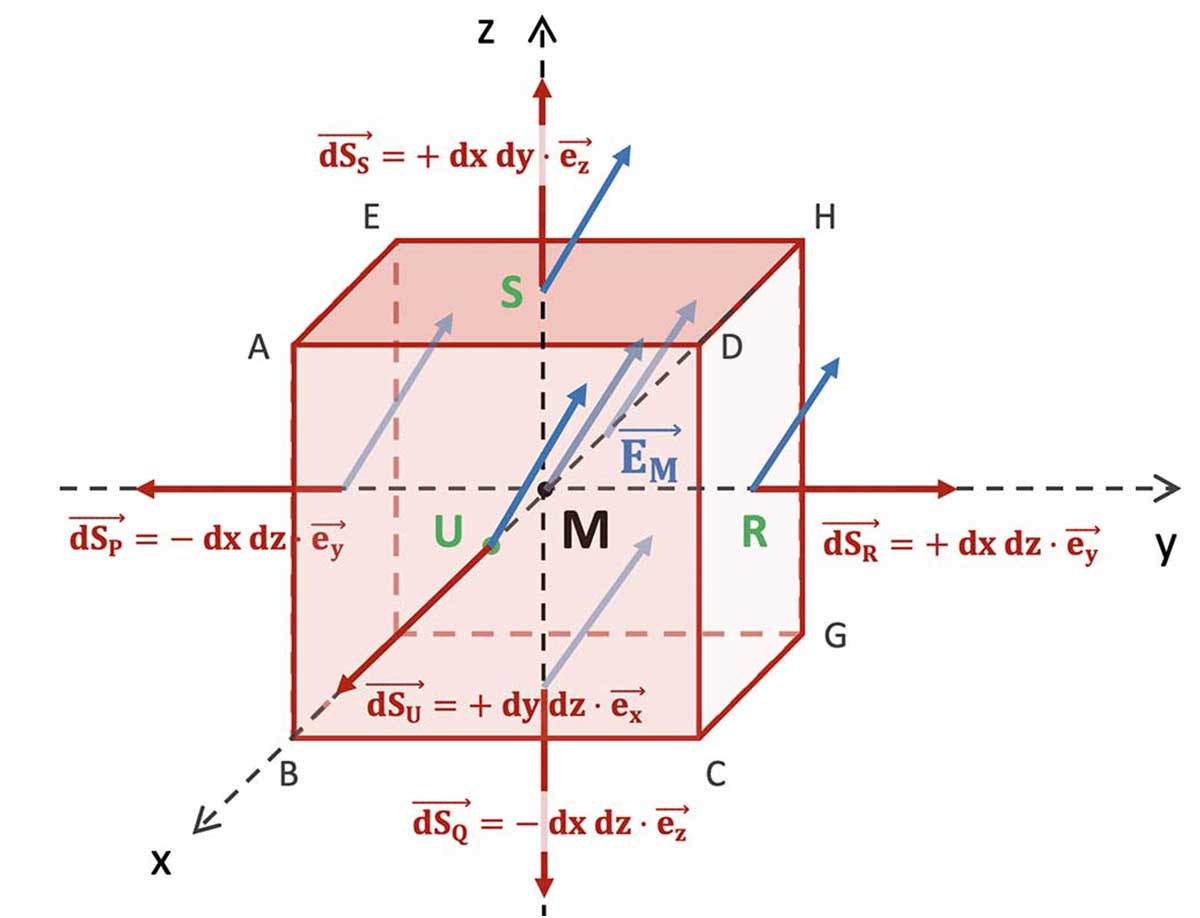
---
* Les *déplacements et surfaces* en jeu étant *infinitésimaux*, au premier ordre et *pour chacune des faces* :
le **champ électrique moyen = champ au centre de la face**.
**$`\mathbf{\quad\quad=\overrightarrow{X_M}\pm\left.\dfrac{\partial \overrightarrow{X}}{\partial x_i}\right|_M\cdot\dfrac{dx_i}{2}}`$**,
champ $`\overrightarrow{X}`$ en $`M`$ plus son taux de variation $`\dfrac{\partial \overrightarrow{X}}{\partial x_i}`$ fois le déplacement élémentaire $`\pm\dfrac{dx_i}{2}`$, positif ou négatif selon le sens du déplacement en direction de l'axe $`Ox_i`$.

---
* La somme des flux sur deux faces opposées selon $`Ox_i`$ donne
$`\left.\dfrac{\partial E_{xi}}{\partial x_i}\right|_M\cdot dx\,dy\,dz`$.
* Le flux total $`\Phi_X`$ à travers les six faces de l'élément de volume donne $`\left(\left.\dfrac{\partial X_x}{\partial x}\right|_M+\left.\dfrac{\partial X_y}{\partial y}\right|_M+\left.\dfrac{\partial X_z}{\partial z}\right|_M\right)\cdot dx\,dy\,dz`$.
* Le produit $`dx\,dy\,dz`$ étant le volume élémentaire $`d\tau`$, selon sa définition l'*expression de la divergence de $`\overrightarrow{X}`$ en coordonnées cartésiennes* s'écrit en tout point de l'espace :
**$`\mathbf{
div\,\overrightarrow{X}}`$**$`\mathbf{\;=\dfrac{d\Phi_X}{d\tau}}`$**$`\;\mathbf{=\dfrac{\partial X_x}{\partial x}+\dfrac{\partial X_y}{\partial y}+\dfrac{\partial X_z}{\partial z}
}`$**
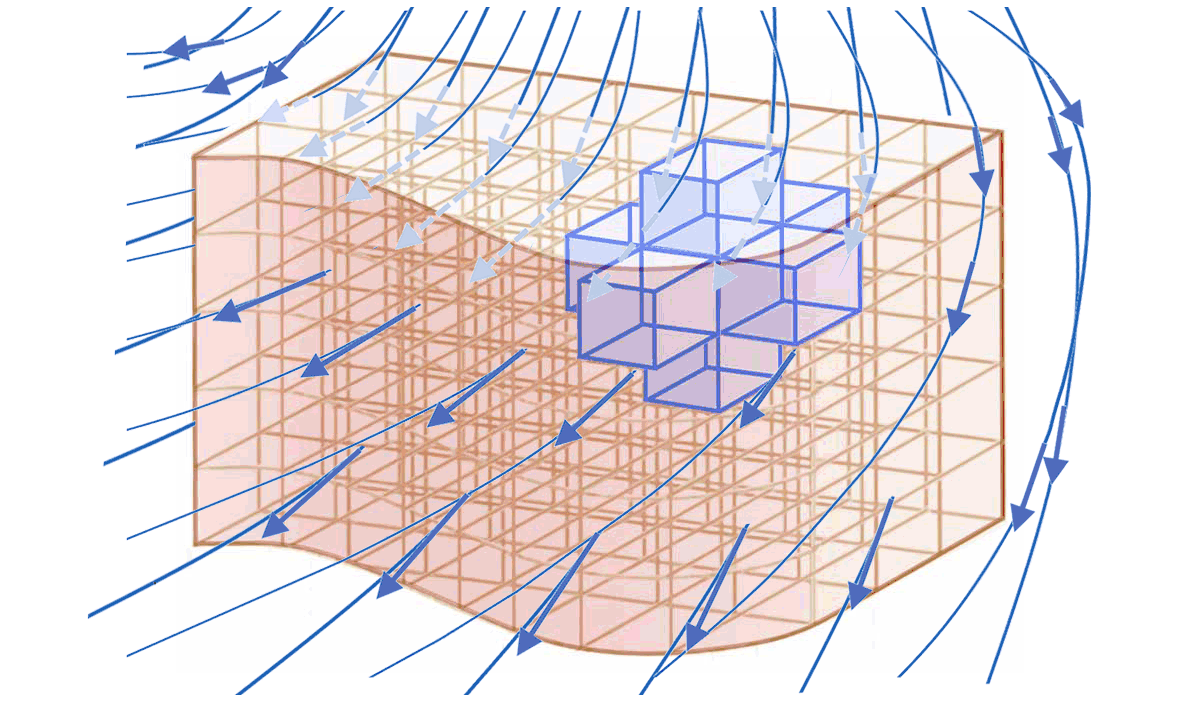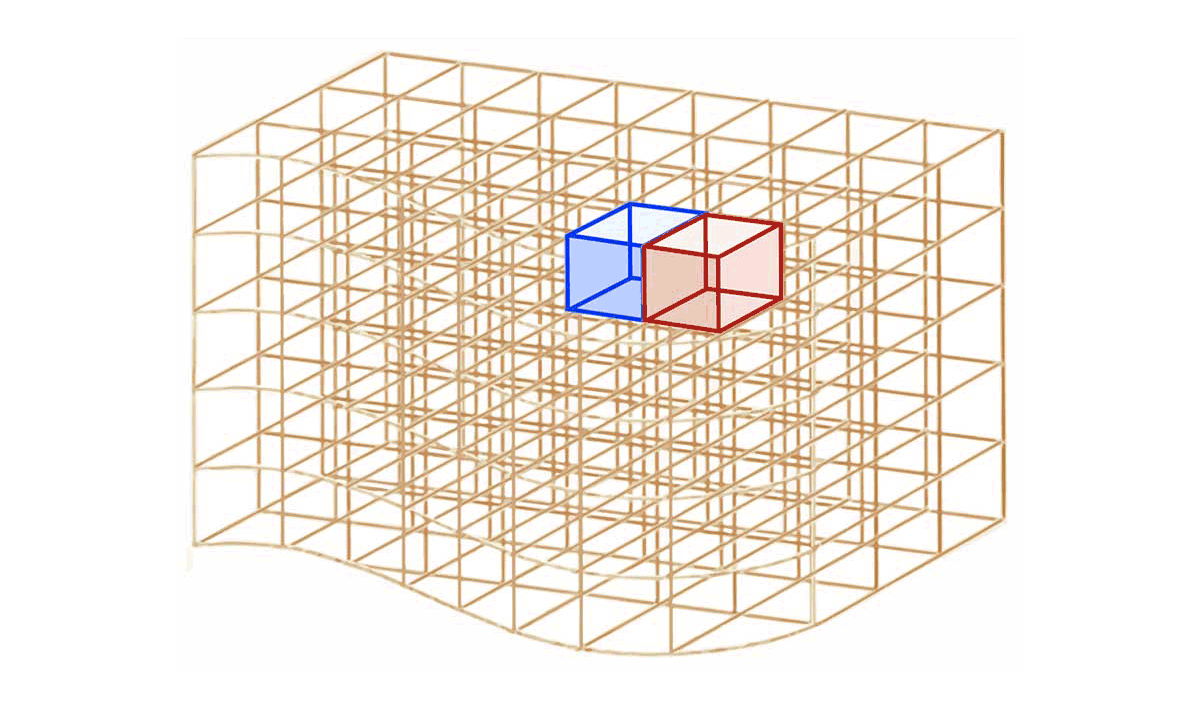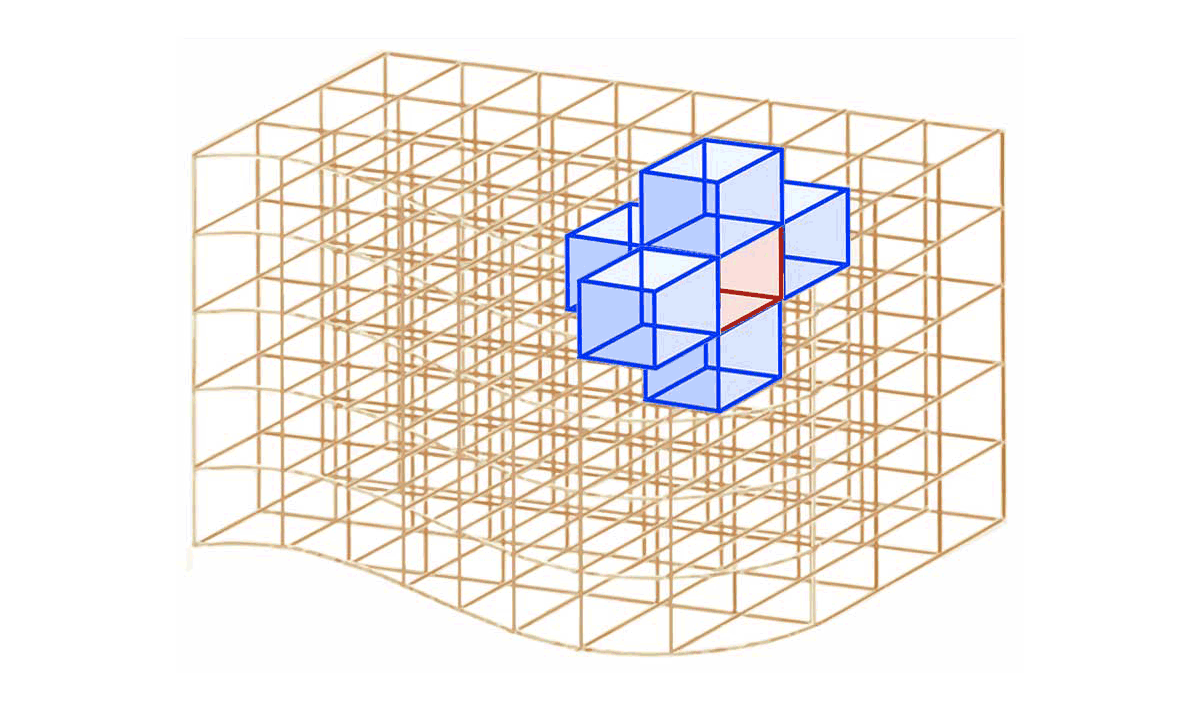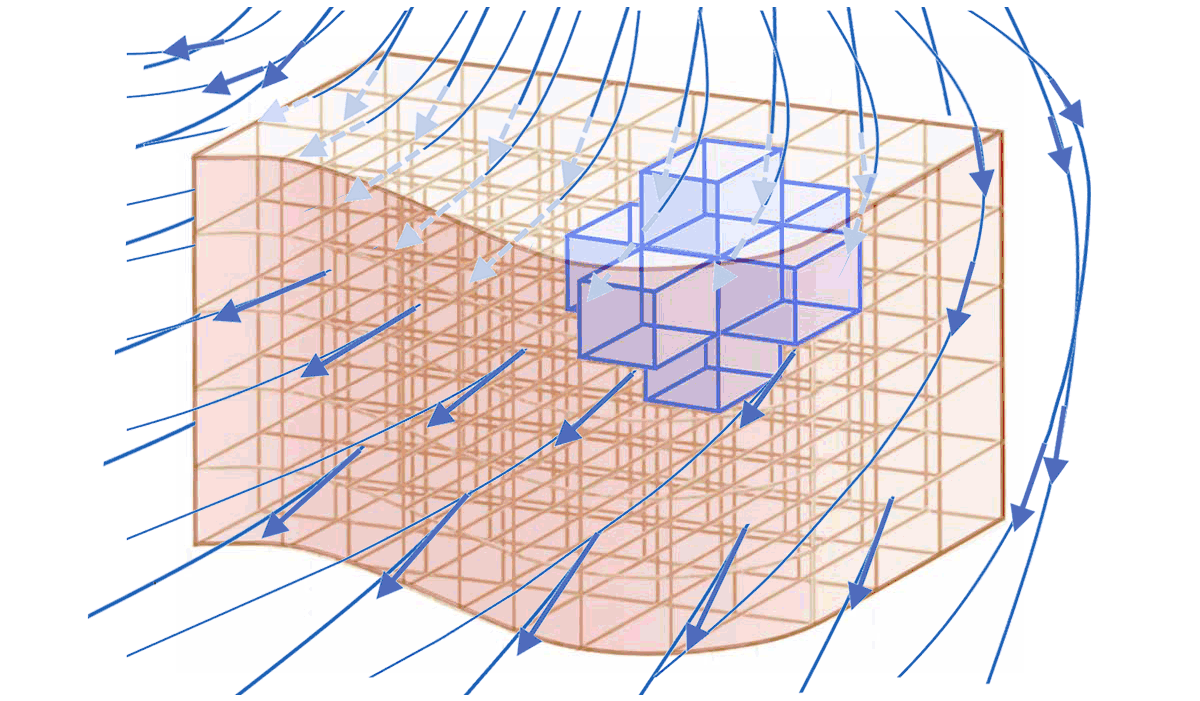
#### Qu'est-ce que le théorème de Green-Ostrogradsky, et comment le visualiser ?
* Soit une **surface fermée $`S`$** dans l'espace *en présence d'un champ vectoriel $`\overrightarrow{X}`$*.
* Soit **$`\Phi_X`$** le *flux de $`\overrightarrow{X}`$* à travers la surface fermée $`S`$.

---
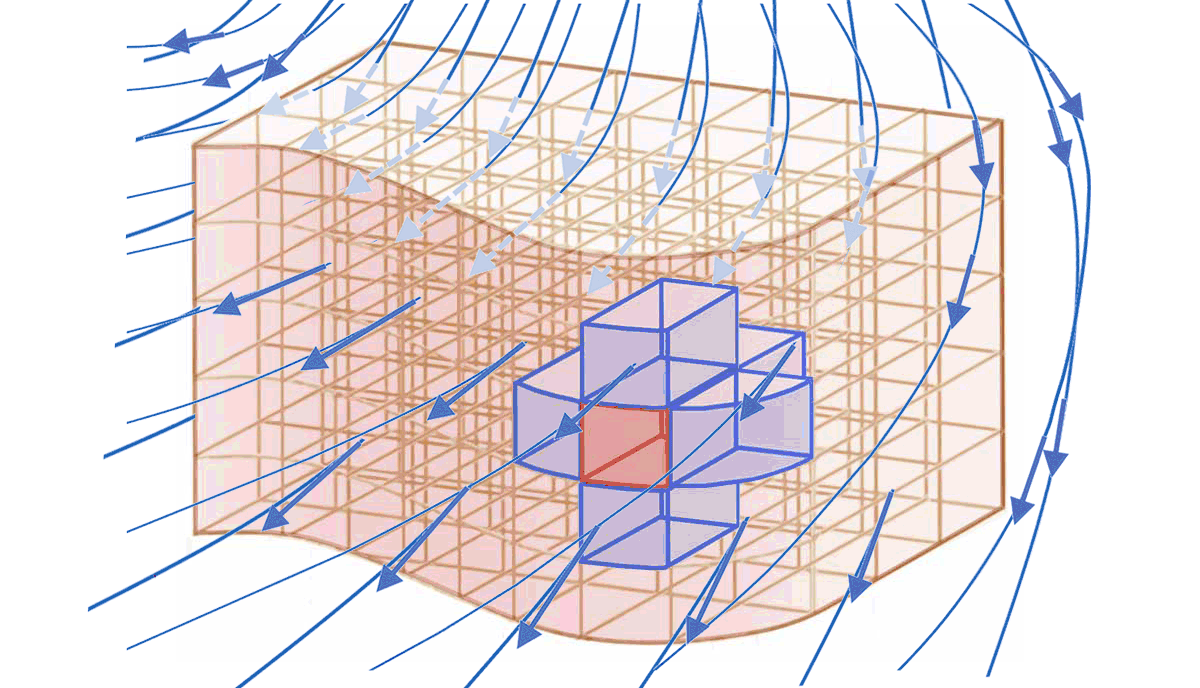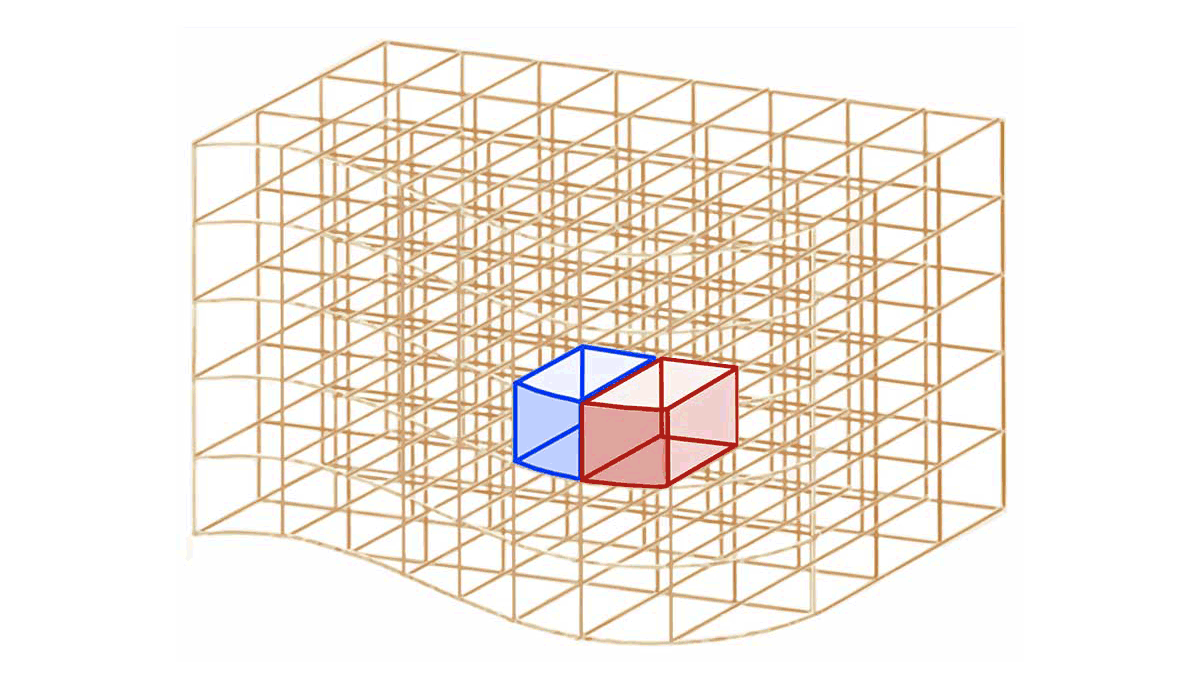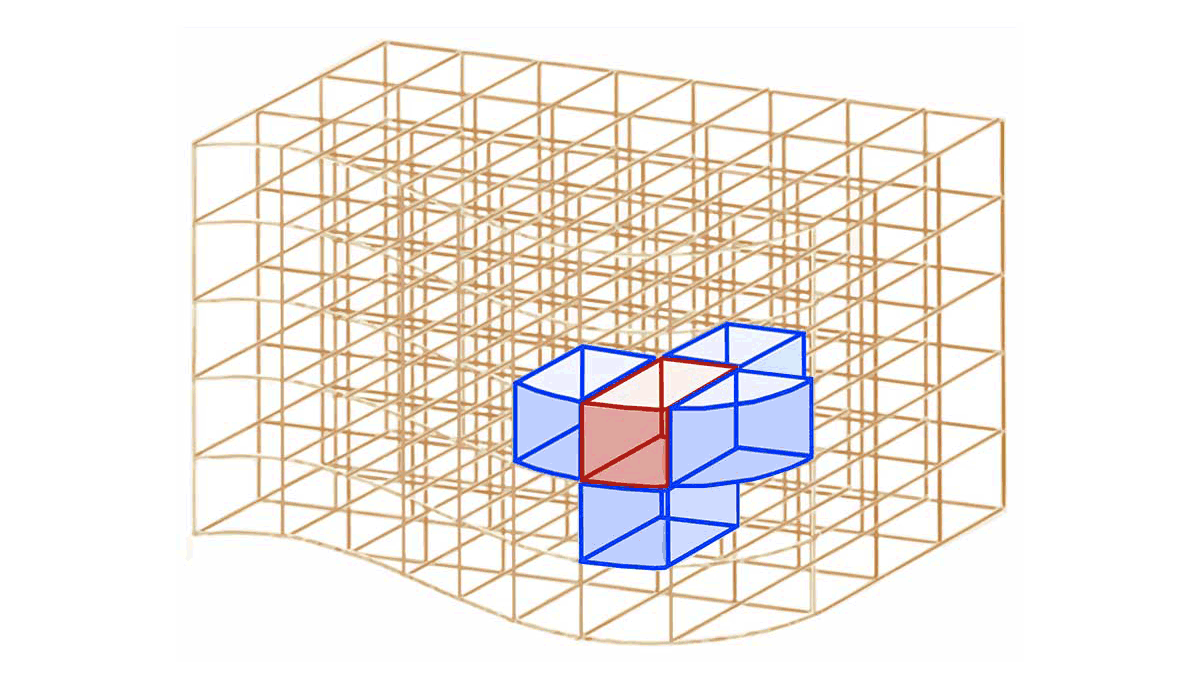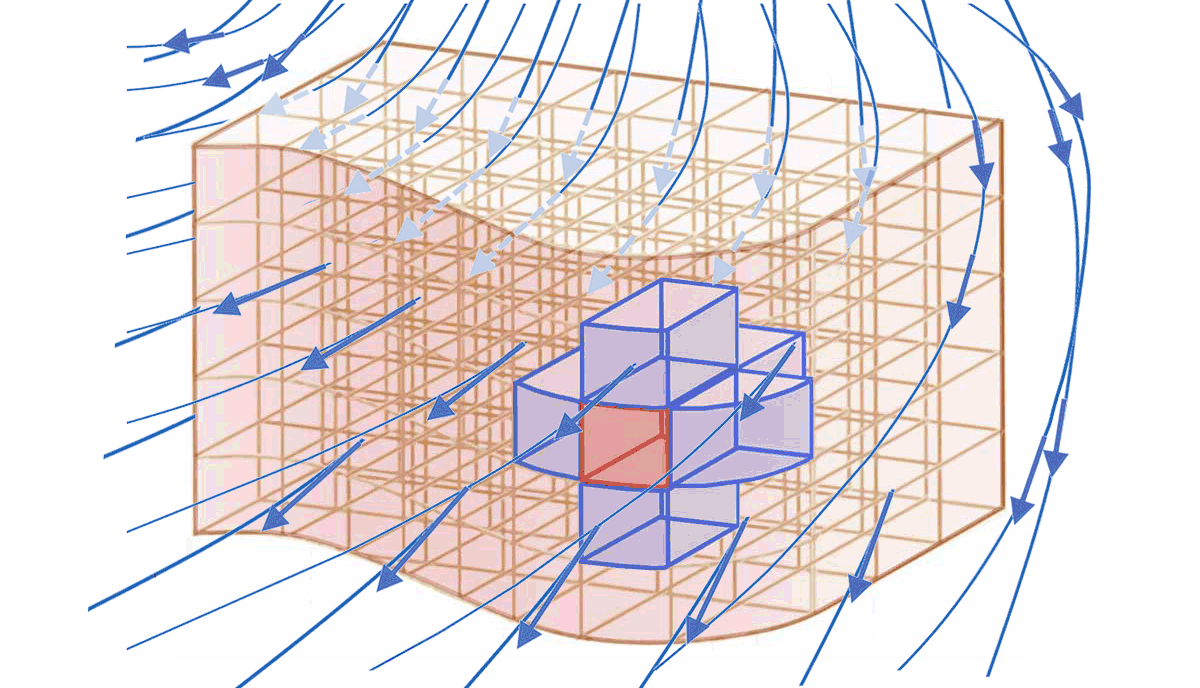
* Le **volume $`\tau`$** que délimite la surface $`S`$ *se décompose* mentalement en *éléments de volume $`d\tau`$*.
* Le champ vectoriel $`\overrightarrow{X}`$ produit un **flux élémentaire $`d\Phi_X`$** à travers chaque *$`d\tau`$* délimité par un élement de surface fermée $`dS`$.
---
* En coordonnées cartésiennes, cylindriques ou sphérique, **chaque élément de surface fermée $`dS`$** associé à un élément de volume $`d\tau`$ qui n'est pas situé en surface du volume $`\tau`$ se décompose en *6 éléments de surface ouverte $`d\Sigma_{int, i}`$* situés *à l'intérieur* du volume $`\tau`$ :
**$`\mathbf{dS=\sum_{i=1}^6 d\Sigma_{int,i}}`$**
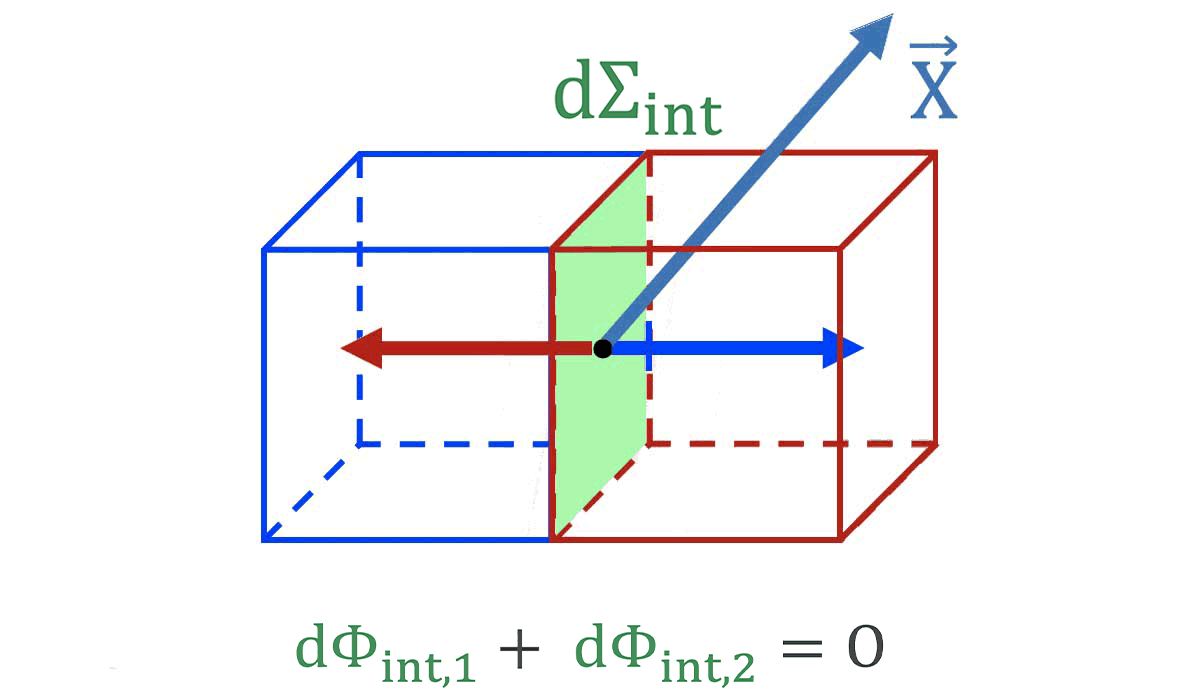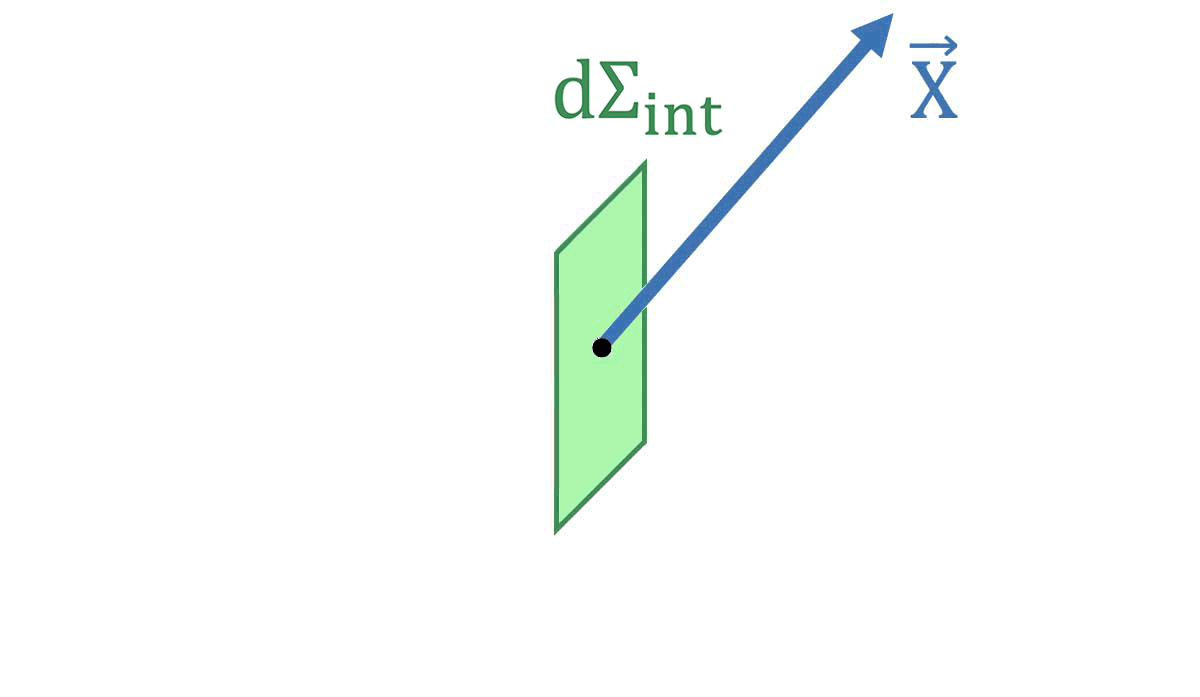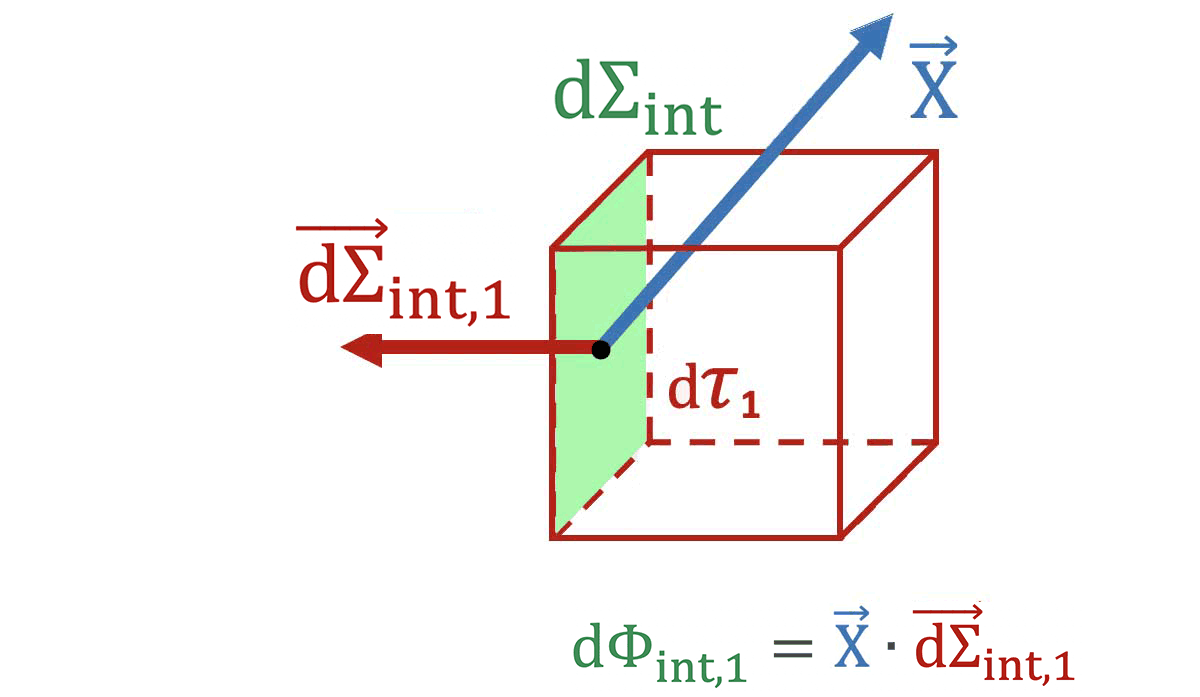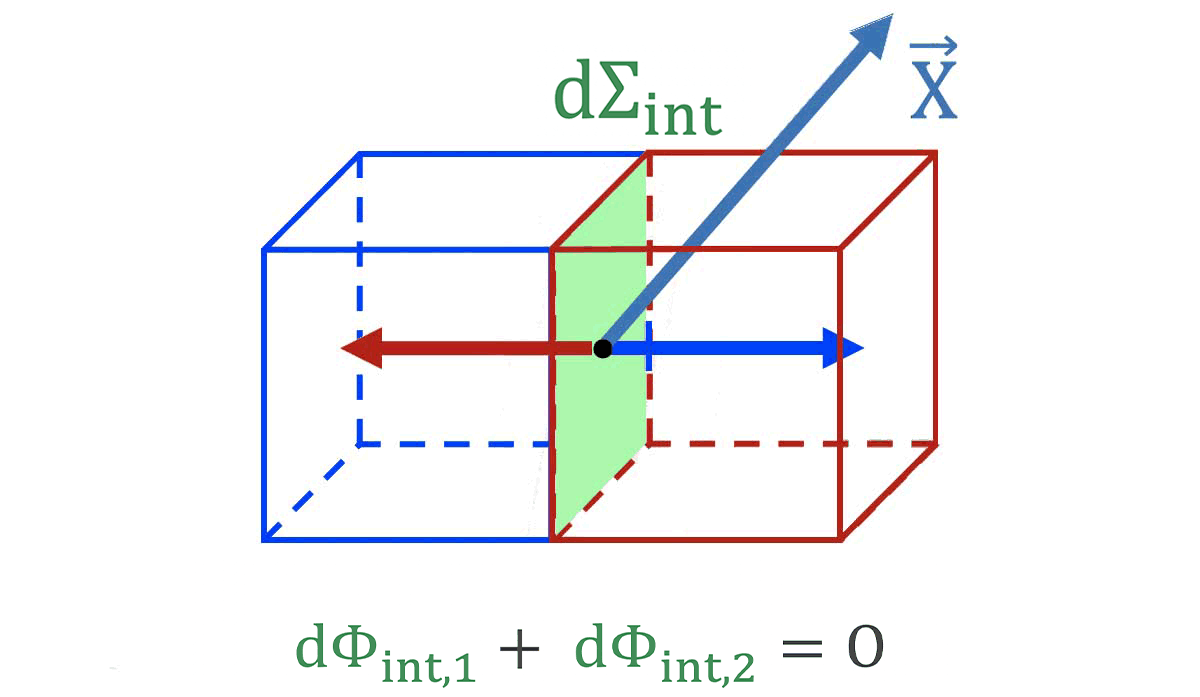
* **A l'intérieur du volume $`\tau`$**, tout élément de surface ouverte $`d\Sigma_{int}`$ appartient à 2 élément de volume $`d\tau_1`$ et $`d\tau_2`$. Selon l'élément de volume considéré, un même élément de surface ouverte intérieure *$`\mathbf{d\Sigma_{int}}`$ est représenté par les vecteurs $`\overrightarrow{\Sigma}_{int,1}`$ ou $`\overrightarrow{\Sigma}_{int,2}`$* qui sont opposés :
**$`\mathbf{\overrightarrow{\Sigma}_{int,2}=-\,\overrightarrow{\Sigma}_{int,1}}`$**
* $`\Longrightarrow`$ les flux élémentaires *$`\mathbf{d\Phi_{int,1}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{int,1}}`$* et *$`\mathbf{d\Phi_{int,2}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{int,2}}`$* correspondants sont opposés :
**$`\mathbf{d\Phi_{int,2}=\,-\,d\Phi_{int,1}}`$**
---
* $`\Longrightarrow`$ le **flux $`\mathbf{\Phi_{int}}`$** de $`\overrightarrow{X}`$ *à travers l'ensemble des $`\overrightarrow{d\Sigma_i}`$ situés* **à l'intérieur** d'un volume (les $`d\Sigma_i`$ appartenant à la frontière extérieure du volume étant exclus) est **nul** :
**$`\displaystyle\mathbf{\Phi_{int}=\int d\Phi_{int}=0}`$**
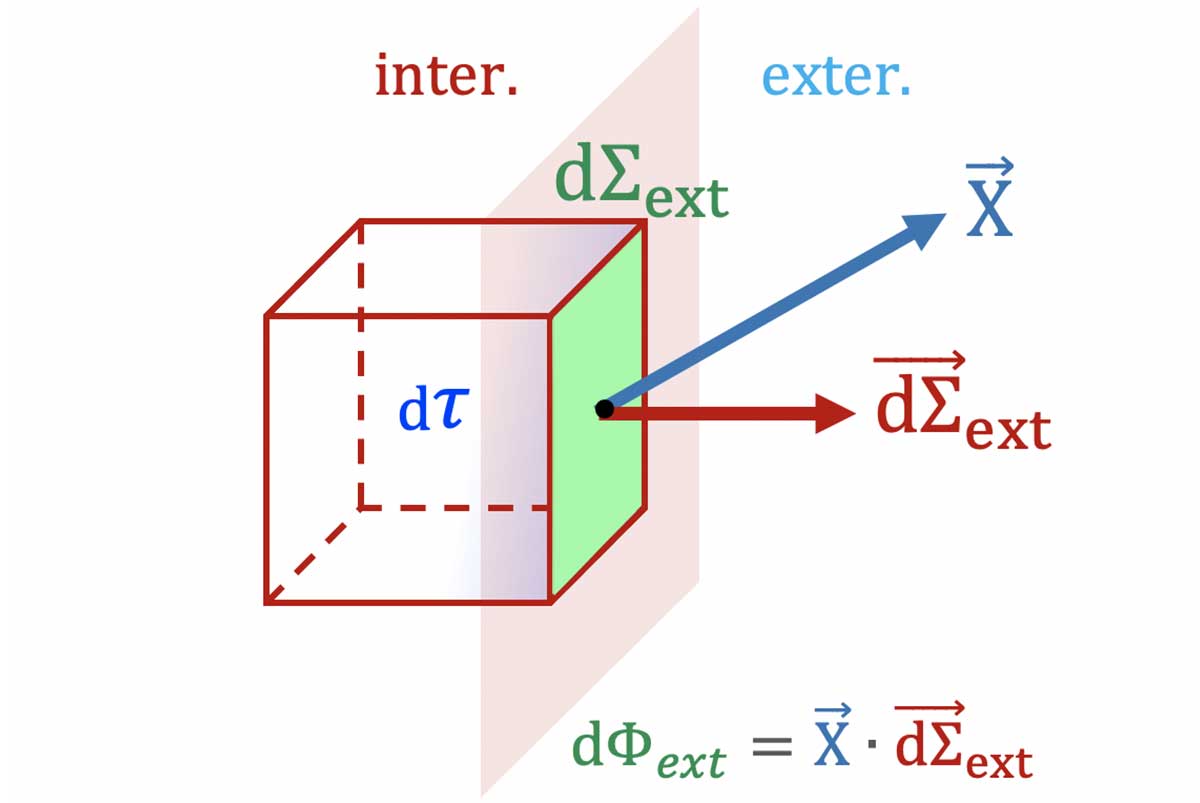
* Tout **élément de volume $`d\tau`$ en contact avec l'extérieur** *possède un élément de surface $`d\Sigma_{ext}`$*. qui appartient à la frontière entre l'intérieur du volume et l'extérieur.
---
* Tout élément de surface $`d\Sigma_{ext}`$ n'appartient qu'à un unique élement de volume $`d\tau`$ du volume $`\tau`$ :
$`\Longrightarrow`$ lui est associé un **unique élément vectoriel de surface $`\overrightarrow{d\Sigma}_{ext}`$** *orienté de l'intérieur vers l'extérieur*.
* $`\Longrightarrow`$ le *flux élémentaire correspondant $`d\Phi_{ext}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{ext}`$* est en général non nul :
*en général*, **$`\mathbf{d\Phi_{ext}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{ext}}\ne 0`$**
* L'ensemble des $`d\Sigma_{ext}`$ est la surface fermée $`S`$ délimitant le volume $`\tau`$ :
$`S=\oiint d\Sigma_{ext}`$
* $`\Longrightarrow`$ le **flux $`\mathbf{\Phi_{ext}}`$** de $`\overrightarrow{X}`$ à travers l'ensemble des $`\overrightarrow{d\Sigma_{ext}}`$ est le flux $`\mathbf{\Phi_X}`$ de $`\overrightarrow{X}`$ à travers la surface fermée $`S`$ délimitant le volume $`\tau`$ :
**$`\displaystyle\mathbf{\Phi_{ext}=\int d\Phi_{ext}=\oiint_S \overrightarrow{X}\cdot \overrightarrow{dS}}`$**
---
* En résumé :
$`\displaystyle\Phi_X=\int d\Phi_X=\int div\,\overrightarrow{X}\cdot \overrightarrow{d\tau}`$
$`\quad=\Phi_{int}+\Phi_{ext}`$$`\displaystyle\quad=0+\oiint_S \overrightarrow{X}\cdot \overrightarrow{dS}`$
* **Théorème de Green-Ostrogradsky**
= *théorème de la divergence* :
**$`\mathbf{\displaystyle\iiint_{\tau \leftrightarrow S} div\,\overrightarrow{X}\cdot d\tau = \oiint_{S \leftrightarrow \Ltau}\overrightarrow{X}\cdot dS}`$**
#### Que devient le théorème de Gauss exprimé localement ?
* Le théorème de Gauss intégral donne :
$`\Phi_X=\oiint_S \overrightarrow{X}\cdot \overrightarrow{dS}=4\pi\,K\cdot \iiint \rho_X\cdot d\tau`$
* Le théorème de Green-Ostrogradsky donne :
$`\Phi_X=\oiint_{S\longleftrightarrow\Ltau} \overrightarrow{X}\cdot \overrightarrow{dS}=\iiint_{\Ltau\longleftrightarrow S} div\overrightarrow{X}\cdot d\tau`$
* Nous en déduisons : $`\iiint_{\Ltau\longleftrightarrow S} div\overrightarrow{X}\cdot d\tau
=4\pi\,K\cdot \iiint \rho_X\cdot d\tau`$
* L'égalité précédente étant vraie pour tout volume $`\tau`$, elle implique l'égalité des intégrandes qui donne le **théorème de Gauss local** :
**$`\mathbf{div\overrightarrow{X}=4\pi\,K\cdot \rho_X}`$**
#### Quelle est l'expression du théorème de Gauss local en électrostatique ?
* En électrostatique : $`K=\dfrac{1}{4\pi\,\epsilon_0}`$, où $`\rho`$ est la densité volumique de charge (exprimée en $`C\,m^{-3}`$ dans le système international d'unités)
* *Théorème de Gauss local* : **$`\large\mathbf{div\,\overrightarrow{E}=\dfrac{\rho}{\epsilon_0}}`$**
#### Quelle est l'expression du théorème de Gauss local en gravitation ?
* En gravitation newtonnienne : $`K=-\;G`$ , où $`\rho`$ est la densité volumique de masse (exprimée en $`kg\,m^{-3}`$ dans le système international d'unités)
* *Théorème de Gauss local* : **$`\large\mathbf{div\,\mathcal{\overrightarrow{G}}=-\,4\pi\,G\,\rho}`$**