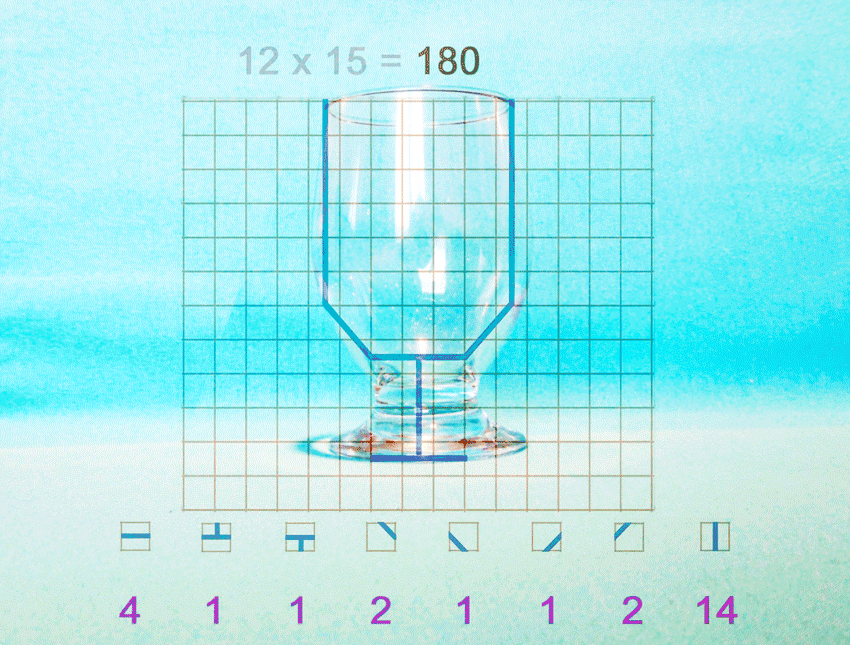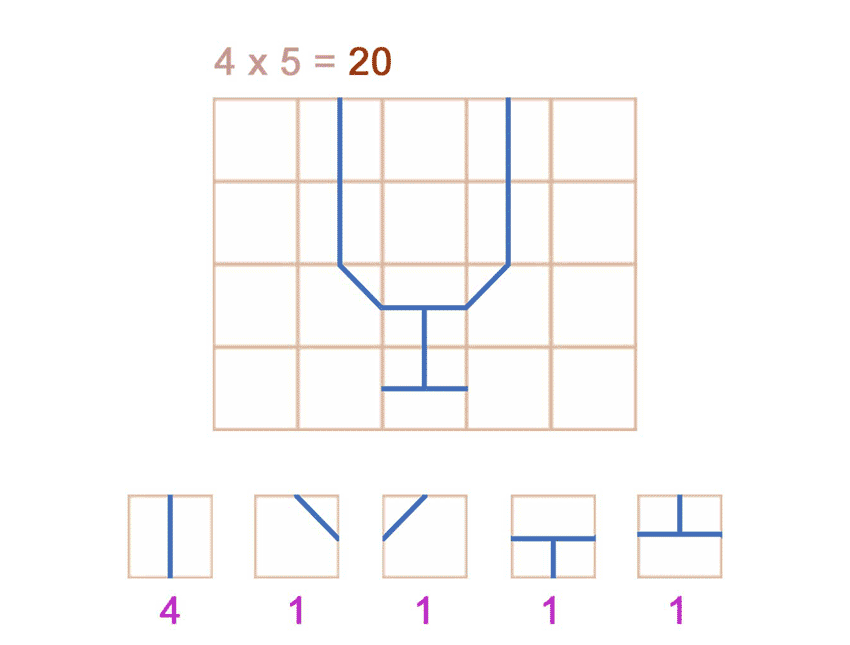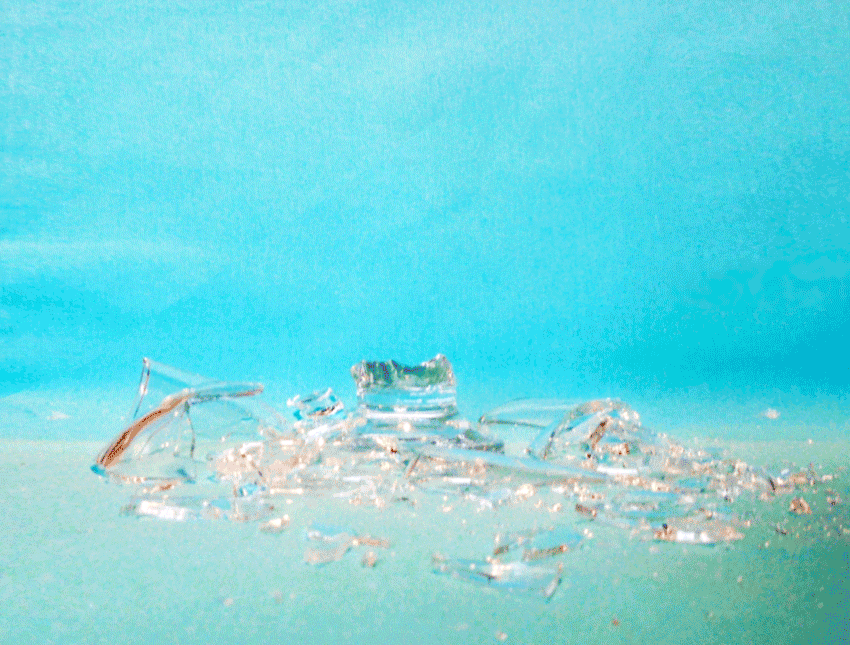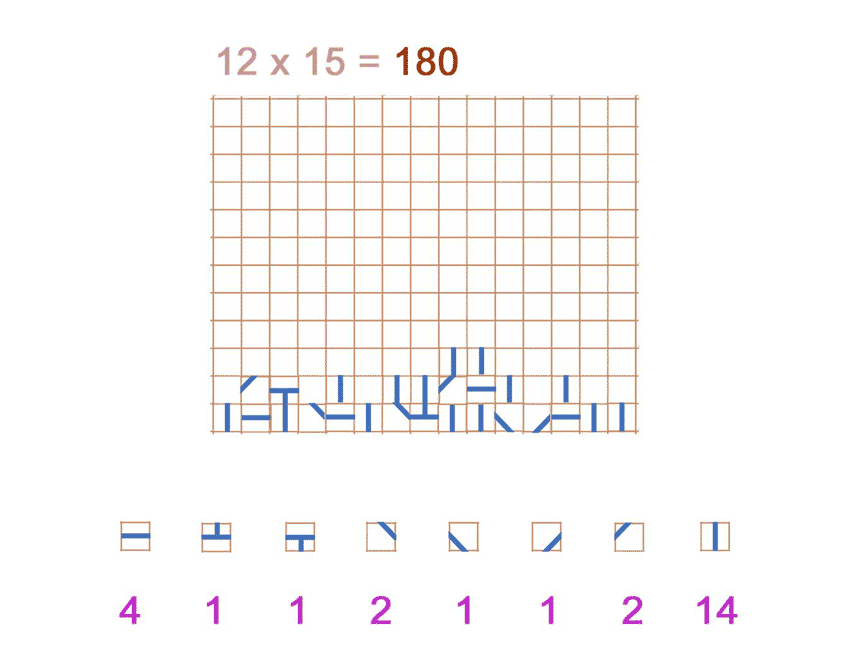courses/00.brainstorming-pedagogical-teams/45.synthesis-structuring/50.entropy/10.n1/20.figures/cheatsheet.fr.md

title	published	routable	visible
<nil>	true	true	false

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

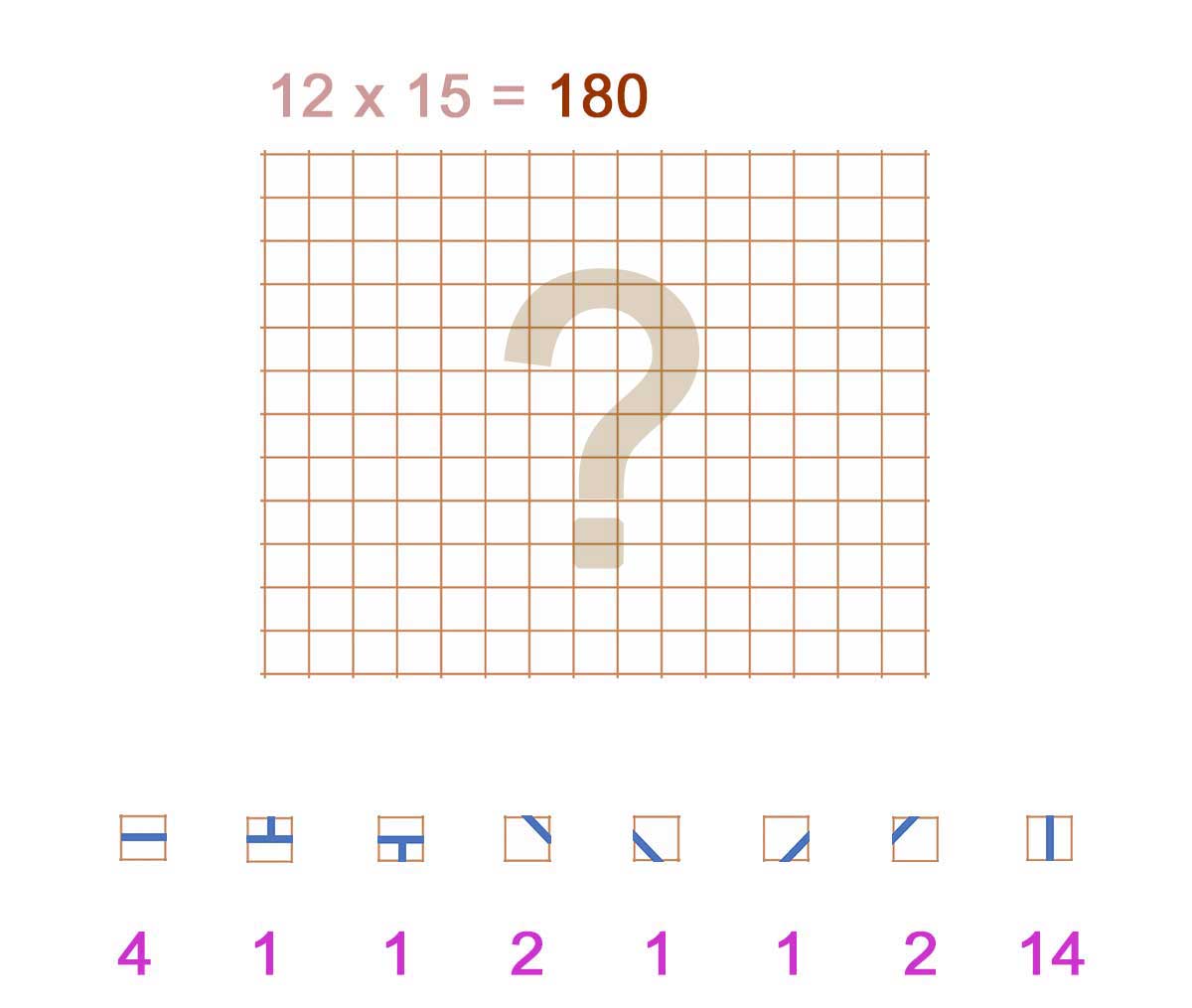
[BR-ENT1&2-10] Pour illustrer le thème des grands nombres

Nécessaire à la seconde loi de la thermo : croissance de l'entropie. Faire prendre conscience que le cerveau humain ne gère absolument pas les grands nombres. Avec la légende de Sissa : Le sage Sissa invente le jeu d'échec pour divertir le roi Belkib. Pour le remercier, le Roi souhaite exaucer le voeu de Sissa. Mettre un grain de riz sur la première case, deux grains sur la deuxième, quatre sur la troisième, 8 sur la quatrième, etc.... en doublant à chaque fois le nombre de grains de riz jusqu'à la dernière case de l'échiquier.

Quelle est la légende de l'échiquier de Sissa ?

Combien de bols de riz faut-il pour remplir l'échiquier ?

J'écris d'abord la formule mathématique qui décrit comment calculer le nombre de grains de riz nécessaires pour répondre au souhait de Sissa :

$\text{nombre de grains requis pour l'échiquier}$

$\quad = \overset{\text{case 1}}{1} + \overset{\text{case 2}}{2} + \overset{\text{case 3}}{(2\times 2)}$ $+ \overset{\text{case 4}}{(2\times 2\times 2)} + ... + \overset{\text{case 64}}{\underset{\text{2 écrit 63 fois}}{\underbrace{(2\times 2\times 2\times ... \times 2)}}}$

Ce calcul ne semble vraiment pas compliqué à faire si tu as un peu ... beaucoup!... de temps. Il ne s'agit que de multiplications par le chiffre 2, et d'additions. Le nombre de grains que tu trouverais est :

$\quad = \text{18 446 744 073 709 551 615 grains}$

C'est un peu plus de dix-huit milliards de milliards de grains de riz.

!! Pour aller plus loin : !! !! Trouver une nouvelle expression plus compacte de ce nombre de grains de riz pour !! un calcul plus rapide avec une calculatrice, en utilisant la fonction puissance $x^y$. !! !! Nomme $N$ le nombre de grains requis pour l'échiquier. !! !! $N = \overset{\text{case 1}}{1} + \overset{\text{case 2}}{2} + \overset{\text{case 3}}{(2\times 2)}$ !! $+ \overset{\text{case 4}}{(2\times 2\times 2)} + ... + \overset{\text{case 64}}{\underset{\text{2 écrit 63 fois}} !! {\underbrace{(2\times 2\times 2\times ... \times 2)}}}$ !! !! Ce nombre peut être réécrit en utilisant la fonction puissance de 2, définie pour toute nombre entier naturel $n$ par !! $2^n=\underset{\text{2 écrit n fois}}{\underbrace{(2\times 2\times 2\times ... \times 2)}}$
!! $2^n$ se dit deux à la puissance n. !! !! $N=1 + 2^1 + 2^2 + 2^3 +\,.\,.\,. + 2^{62}$$\; + 2^{63}$$\;\quad (equ.1)$ !! !! Tu as le droit de multiplier les deux membres (gauche et droit) de cette égalité par un même nombre réel. Ainsi cette égalité écrite restera vraie. Multiple les par 2 : !! !! $N \times 2 = 1 \times 2 + 2^1 \times 2 + 2^2 \times 2 $$\;+ 2^3 \times 2 + \,.\,.\,. + 2^{62} \times 2 + 2^{63} \times 2$ !! !! Mais par définition : !! !! $2^n \times 2 = \underset{\text{2 écrit n fois}}{\underbrace{(2\times 2\times 2\times ... \times 2)}}\times 2$ !! $\quad = \underset{\text{2 écrit n+1 fois}}{\underbrace{(2\times 2\times 2\times ... \times 2)}}=2^{n+1}$ !! !! Tu peux donc réécrire !! !! $N \times 2 = 2 + 2^2 + 2^3 + 2^4 + \,.\,.\,. + 2^{63}$$\; + 2^{64}\quad(equ.2)$ !! !! Tu peux maintenant comparer les équations $(equ.1)$ et $(equ.2)$, et remarquer que !! !! $2 + 2^2 + 2^3 + 2^4 + \,.\,.\,. + 2^{63} + 2^{64}$$\; = (1 + 2^1 + 2^2 + 2^3 +\,.\,.\,. + 2^{62} + 2^{63})$$\;-1+2^{64}$ !! !! donc $N \times 2 = N - 1 + 2^{64}$ !! !! $(N \times 2) - N = 2^{64}- 1$ !! !! soit au final $N = 2^{64}- 1$. !! !! Pour ce calcul, une calculatrice avec suffisamment de chiffres d'affichage donnerait $2^{64}=18\,446\,744\,073\,709\,551\,616$. !! !! Peu de calculatrices affichent autant de chiffres, car un résultat affiché avec autant de précision n'a pas vraiment d'intérêt.
!! Une calculatrice standard affiche par exemple :
!! $N=18\,446\,744\,073\,709\,55e19$
!! Le "e19" signifie que pour obtenir le nombre affiché, il faut reculer la virgule vers la droite de 19 positions, en ajoutant des $0$ si nécessaire. Tu pourrais ainsi écrire :
!! $N=1,844674407370955e19$$\quad N=18446744073709550000$
!! Comme tu le vois, tu perds la précision sur les 4 derniers chiffres ($0000$ eu lieu de $1615$. !! !! En fait, afficher un résultat avec une erreur de $1615$ sur plus de 18 milliards de milliards n'a aucune importance. Seul l'ordre de grandeur est important, et pour afficher celui-ci, 2 chiffres significatifs sont suffisants en général. Les chiffres significatifs sont les chiffres les plus à gauche et différents de $0$. Tu écriras ainsi : !! !! $N\sim 18\,000\,000\,000\,000\,000\,000$ !! !! où mieux encore sous forme de puissance de dix : !! !! $N\sim 1,8^{19}$, ou encore $N\sim 18^{18}$ (dans ce dernier cas, la puissance 18 t'indique directement le nombre de 0, ce qui évite de les recompter). !! !! Une telle somme, qui commence par un entier $a$ et dont chaque terme est le produit du terme suivant par un entier b est appelée suite géométrique de premier terme a et de raison b.
!! Les étapes du calcul précédent sont la base pour établir un résultat très général concernant les suites géométriques.
!! La suite géométrique sera dans le programme du prochain niveau "collines".

Il faudra expliquer le symbole $\sim$

C'est un nombre énorme ! Combien de ... tonnes de riz cela représente-t-il?

Estimation de la masse de riz que cela représente

Essaye de réfléchir à ce que représente ce nombre $2^{64}$, en évaluant à la louche, avec une petite expérience que chacun peut faire, la masse de riz que cela représente :

Une méthode serait de :

• mesurer approximativement la masse de 100 grains de riz.
• en déduire par une règle de trois la masse de $2^{64}$ grains de riz.
• trouver sur internet des informations qui permettent de se représenter la signification mentale d'une telle quantité de riz.

Méthode : mesure de la masse de 100 grains de riz. Incertitude de mesure très grande, mais pas d'incertitude au niveau 1. Et ce n'est pas l'objectif de ce chapitre au niveau 2. Donc on prend le symbole $\sim$ qu'il faudra expliquer.

$\text{masse de 100 grains de riz}\sim 3\,\text{grammes}$

$\text{masse totale de riz}$$\;\;\;\sim\dfrac{\text{nombre de grains}}{100}\times \text{masse de 100 grains}$

$M_{riz}= \dfrac{18\;446\;744\;073\;709\;551\;615}{100}\times 3\,g$

$\text{masse de 100 grains de riz}\sim 3\,\text{grammes}$

$\text{masse totale de riz}$$\quad\sim\dfrac{\text{nombre de grains}}{100}\times \text{masse de 100 grains}$

$M_{riz}= \dfrac{18\;446\;744\;073\;709\;551\;615}{100}\times 3\,g$

=...

à continuer :

Ramenez au temps qu'il faudrait pour compter ces grains, ou pour observer l'évènement "le dernier grain sur la 64ème case est posé".

Si on dépose un grain par seconde (à supposer qu'il soient disponibles à souhait), il faudrait $10^{18}$ secondes.

• 30 années sont approximativement $10^9$ secondes.
• 1 vie humaine représente donc approximativement $3\times 10^9$ secondes.
• Construction de la pyramide de Khéops : ...
• extinction de dynosaures : ...
• âge de l'Univers (depuis le Big Bang) : ...

Avec l'idée de montrer que si la fréquence d'un évènement est trop faible, même si mathématiquement elle n'est pas nulle, en pratique elle ne s'observera jamais.

---

[BR-ENT1&2-20] Ce à quoi on est sensible

à faire

---

[BR-ENT1&2-30] Tirage ordonné, tirage désordonné

Sommes-nous sensibles, ou accordons-nous une valeur particulière à un tirage ordonné (dans les jeu de cartes, non) par rapport à un tirage désordonné ?

• ensemble, contient des éléments, pas d'ordre.
  Notation {...}

• suite : ensemble d'éléments ordonnés
  Notation (...) (une suite d'instruction ne fonctionne que si les instructions sont réalisées dans l'ordre chronologique)
  
  pour niveau 2 : dans une base de vecteurs $(\overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3})$, l'ordre des vecteurs est important (on différencie les bases directes et indirectes).

---

[BR-ENT1&2-30] Probabilité et temps moyen de réalisation

Jeu de 6 cartes (as, 2, 3, 4, 5, 6)

Ensuite parler de n tirages de 6 cartes successifs, probabilité de réaliser n tirages successifs de l'as par exemple.

Se représenter l'ordre de grandeur des puissances de 6. Lier à un travail sur les bases numériques (base 2, base 10, donc base 6, ect...)

A venir, figures de 1, 2, 4, 8, 12 et 16 tirages successifs dans un jeu de 6 cartes (ou lors du lancé d'un dé).

Durée statistique moyenne entre deux évènements "tirage de n as succesifs", combinaison gagnante.

Montrer que si $6^{15}$ (n=15) est un nombre "grand",
ce n'est pas encore un "grand nombre" en terme de physique statitique (il y a autour de $`10^{22} atomes dans tout centimètre cube de matière).

---

[BR-ENT1&2-40] Macroétat "gagnant" et macroétat "perdant", dégénérescence, probabilités et durée moyenne entre deux réalisations.

A priori (à discuter), ne pas utiliser le vocabulaire "macroétat, microétat, dégénérescence, ..." à ce niveau 1 (ou alors l'aborder dans un aparté "au-delà").

Vocabulaire "évènement, réalisation, probabilité, durée statistique moyenne entre deux tirages gagnants" ?

Mettre avant la "durée d'un tirage de 4 cartes".

Précisez ce à quoi on est sensible :

• (type, valeur) $\Longrightarrow\quad N=52$ microétats dans le jeu.
  
• (couleur, valeur) $\Longrightarrow\quad N=26$ microétats dans le jeu.
• (valeur) $\Longrightarrow \quad N=13$ microétats dans le jeu.

Calcul du nombre de microétats pour un tirage ordonné ou non de 4 cartes :

• (type, valeur) $\Longrightarrow\quad N=52\times 51 \times 50\times 49$ microétats dans le jeu.
  
• (couleur, valeur) $\Longrightarrow$ pas si simple ...
• (valeur) $\Longrightarrow$ pas si simple ...

Quel niveau? Que dire au niveau 1?

Calcul de la probabilité des microétats équiprobables : 1/N

Dégénérescences des macroétats "gagnant" et "perdant".

Calcul de la probabilité du macroétat "gagnant", du macroétat "perdant".

Duréestatistique moyenne entre 2 macroétats "gagnants".

Quelque-soit ce à quoi on est sensible, plus de chance d'être perdant que gagnant.

Ce qui se passe si $\quad\dfrac{\text{dégénérescence "gagnant"}}{\text{dégénérescence "perdant"}} \rightarrow 0$

La durée statistique moyenne entre deux tirages gagnants tend vers l'infini.

Quelque soit ce à quoi on est sensible, nous tendrons à être toujours perdants

---

[BR-ENT1&2-50] Pour illustrer le thème de la flèche du temps, croissance de l'entropie

Entropie, l'exemple classique du verre qui se briseet ne se reconstitue jamais*.

Exemple que nous suivrons sur les 4 niveaux, tant il y a à développer et dire.

C'est l'exemple type toujours utilisé pour illustrer la notion d'une entropie qui ne peut que croître. Et tous les exemples sur ce thème le traitent à peu près de la même façon, alors que c'est vraiment le thème que l'on peut développer du niveau 1 au niveau 4. Il y a pleins de choses à dire, de complexité et réflexion croissantes, des niveaux 1 à 4. On va le faire.

Première réflexion et modélisation

Premières modélisations, réalisées par un observateur plus ou moins myope.

(Idée : Amener progressivement la seconde loi de la thermodynamique macroscopique, l'idée que dans un système isolé caractérisé par un grand nombre de configurations équiprobables possibles, l'entropie (grandeur extensive) ne peut que croître, et que le fait de cette croissance ne dépend pas du niveau de précision ou de connaissance dans la description du système.)

Parler d'ordre ou de désordre est trompeur

_Pour arriver aux niveaux 3 ou 4 que l'entropie ne mesure pas un "ordre", mais la probabilité $P(\Omega_0)$ d'un état macroscopique $\Omega_0$ (caractérisé par des variables macroscopiques), correspondant à un nombre $Nb(\Omega_0)$ de micro-états $\omega_{0\,i}$ de probabilités individuelles $P(\omega_{0\,i})$, tels que ... à construire, progression à mettre au point sur tous les niveaux.

Pour un observateur qui voit le verre en 8 parties dans un espace isolé de 20 positions spatiales :

Chacune des configurations spatiales des "morceaux" est unique et équiprobable (hypothèse à débattre), les 5 présentées sont équivalentes.

• Trois nous "semblent" désordonnées.
• Une représente le verre non brisé
• Une représente une sorte de configutation non reconnaissable, mais semblant "ordonnée".

Comment attribuons-nous une "valeur particulière" à une configuration plutôt qu'à une autre ?

• subjectivité
• configuration macroscopique spatiale permettant une utilité : le verre non brisé
• configuration d'un système macroscopique caractérisé par des valeurs fixes ou de valeurs d'équilibre de variables macroscopiques.
• un sens peut-être attribué : par exemple décodage d'un message. ("Ceci est un message" est une série de 19 caractères alphanumériques. Si comme caractère alphanumérique on compte 26 lettres de l'alphabet, 10 chiffres et le blanc, soit 37 caractères alphanumériques, il y a $26^{19}$ séries possibles. La probabilité de trouver un message intelligible si les caractères sont tirés au hasard, est infinitésimale).
• autre ?

Sur le rôle des ... interactions, contraintes physique, ici si on considère que l'axe verticale est l'altitude. Les morceaux brisées ne sont "pas lancés en l'air", mais "repose sur le sol".

• 3 configurations ont la même énergie potentielle (hypothèses simplificatrices)
• l'autre configuration est le verre non cassé

Combien de configurations ?

Pour un observateur qui voit le verre en 26 parties dans un espace isolé de 180 positions spatiales :

Chacune des configurations spatiales des "morceaux" est unique et équiprobable (hypothèse à débattre), les 5 présentées sont équivalentes.

• 3 nous "semblent" désordonnées.
• 1 représente en bous le verre non brisé
• 1 représente une sorte de configutation non reconnaissable, mais ordonnée.

Sur le rôle des ... interactions, contraintes physique, ici si on considère que l'axe verticale est l'altitude. Les morceaux brisées ne sont "pas lancés en l'air", mais "repose sur le sol".

• 3 configurations ont la même énergie potentielle, presque minimale (hypothèses simplificatrices).
• l'autre configuration est le verre non cassé

Combien de configutations ?

(Idée : Il y aura des contre-exemples en physique des matériaux au niveau 3 ou 4, qui montreront que ce terme d'ordre peut être trompeur).

une autre avec un verre réel et l'expression interlinguistique : [FR] "casser le verre en mille morceaux" ... [ES] "rompe en mil pedacitos, o ... rompiendo el vidrio en mil pedazos" [EN] "shattered into a thousand pieces"

1000 morceaux : équivalents des 5 ou 8 morceaux des exemples 2D dessinés

Puis ensuite ...

118 éléments chimiques : : équivalents des 5 ou 8 morceaux des exemples 2D dessinés, ou des milles morceaux.

Montrer, dès ce niveau 0, que le dénombrement dépend de la résolution, mais pas la seconde loi de la thermo... que ce soit avec des mots de tous les jours à ce niveau 1.

---

[BR-ENT1&2-70] On aura besoin de l'hypothèse ergodique

Même si on ne la nomme pas aux niveau 1 et 2, peut-être simplement la citer déjà au niveau 2 dans un aparté "au-delà" ?

L'hypothèse pose $p^{suc.}\{a, b, c\}=p^{sim.}\{a, b, c\}$
$a, b, c$ sont les trois résultats des trois tirages individuels,
et $\{a, b, c\}$ est l'ensemble constitué par ces trois résultats
(ensemble, donc non ordonné).

De même, en associant à l'ordre chronologique des trois tirages individuels successifs, un ordre spatial des trois tirages simultanés, on aurait :
$p^{suc.}(a, b, c)=p_{sim.}(a, b, c)$
où $(a, b, c)$ est une suite ordonnée des trois résultats individuels.

Enfin, on précisera tout cela dans les niveaux. Mais déjà ce sera utile si l'internaute souhaite faire des études statistiques et qu'il n'a qu'un seul jeu de carte...

[BR-ENT1&2-80] Essai de visualisation sur smartphone

Sujet : dénombrement des séquences ordonnées (suites) et des séquences non ordonnées correspondant à trois tirages successifs d'une lettre prise dans l'ensemble $\{A,B,C\}$.

Granulation de l'espace des possibles si l'on est sensible à l'ensemble (non ordonné). Chaque grain a une surface proportionnelle à sa probabilité d'apparition.

En physique, les systèmes évoluent lentement au cours du temps (calcul différentiel, $df/dt$). Si on monte dans les niveaux, et on applique cela à la théorie cinétique des gaz de Boltzmann, avec l'espace des phases, vers alors on va vers les notions de libre parcours moyen, de temps moyen entre deux collisions, de transition vers l'équilibre lorsque un grain correspond à une probabilité qui tend vers 1. A construire.

[BR-ENT1&2-80] Essai de visualisation sur smartphone (des repères chronologiques)

Idée des fresques :

• créer des fresques chronologiques :

  • étendues sur différentes durées (et donc exprimées en différentes unités : "univers", années, jours, secondes, nanosecondes, etc...).
  • rétrospectives depuis l'instant présent (symbolisé par le personnage qui regarde vers le passé).
  • réalisées en échelle logarithmique (pour une vision plus large, avec aussi l'idée que et l'importance accordée, et la précision historique, décroissent avec le temps).
  • avec des références historiques culturelles fortes sous formes de symboles relativement compréhensibles relativement à l'évènement ou la période qu'ils représentent.

• avec les objectifs de :

  • rendre compte des durées (intuition des grands nombres, des très grands nombres (vers la notion d'irréversibilité, et d'état d'équilibre), des très petits nombres, des constantes de temps.
  • situer chronologiquement, donner de la profondeur historique (depuis l'antiquité grecque, la démarche scientifique est une des plus vieille construction culturelle humaine), situer les étapes scientifiques (en marron rouge) et technologiques (en bleu) qui marquent une thématique scientifique (exemples : optique géométrique, optique ondulatoire, mécanique Newtonienne, mécanique quantique, relativités, évolution des idées sur "l'espace, le temps, la matière, l'énergie", etc).

• réutilisables dans différentes disciplines :

  • Pour une étendue temporelle donnée (exemple de la figure : de l'instant présent à 1 milliard d'année dans le passé), une seule ou 2 ou 3 fresques maximum, utilisables un grand nombre de fois, dans plein de matières différentes.
  • L'utilisation dans une matière spécifique (exemple : optique géométrique) se fera en introduisant entre la partie haute de la fresque (l'échelle logarithmique des temps, en vert) et la partie basse de la fresque (les références temporelles fortes en marron-rouge ou bleu),
    introduction d'une partie spécifique à la matière sous forme d'une ligne de petits triangles pointent vert une date et de petits rectangles qui indiquent une période (marron-rouge pour une découverte scientifique, bleau pour une invention technique).
    Pour chaque date ou période indiquée, quelques mots décrivant la découverte ou l'invention correspondante, dans une liste (sous forme fixe ou de menu déroulant) placée à la suite de la fresque.
    Si nécessaire, un texte développant cet historique peut être développé dans la partie main du cours.

• 1, 2 ou 3 fresques maximum par étendue temporelle

  • une seule suffit
  • une 2ème ou 3ème autres peuvent se justifier. Par exemple dans une discipline liée à l'information ou à l'informatique, il peut se justifier de remplacer la période référence historique "1480-1525" ( découverte par voie maritime de l'Amérique par les européens, première circumnavigation de l'histoire par Fernand de Magellan) historique "découverte par voie maritime de l'Amérique par les européens") par la période référence historique et temporellement voisine "1000-1450" (inventions du caractère mobile d'imprimerie et de l'imprimerie, Bi-Sheng, Jikji, puis bible de Gutemberg).

• Des références temporelles universelles.

  • La longue période (mais courte dans l'échelle logarithmique) de sortie de la vie végétale et animale des océans est vraiment une référence temporelle universelle.
  • Autre exemple, l'icône :
    
    

• Des références temporelles à défaut adaptées à chaque culture.

  • Exemple 1, dans le texte succinct de description de l'icône :
    
    - Si La traduction française est portée par le continent européen, on peut faire appel à la référence culturelle européenne "découverte du continent américain par l'Européen Christophe Coulomb".
    - Et si la traduction en espagnol est portée par l'amérique du sud et centrale, on peut parler du "chocs des empires Maya et Incas avec les conquistadors", et peut-être remplacer Christophe Coulomb par Cuauhtémoc, Cortés, Huáscar, Atahualpa, Pizarro.
    Les "porteurs" d'une langue choisirons leurs références temporelles.
    A discuter : de toute façon, le site M3P2 est évolutif, cela pourra évoluer, piloté par les équipes pédagogiques, et validé par les universités partenaires.
  • Exemple 2 : L'icône des "pyramides de Khéops" peut être remplacée par l'icône d'une azturia ou autre, si c'est plus parlant en amérique latine (en terme d'importance culturelle et repérage chronologique, je ne sais pas).

[BR-ENT1&2-80] Essai 2 de visualisation sur smartphone

Essai pour séparer un figure en plusieurs parties jointes (pour séparer une partie purement image d'une partie texte qui diffèrera selon la langue).

• figure complète (comprend les parties 1 2 et 3 dans un tout)

• Succession des 3 figures, chacune correspondant à une partie.

Vérifier vocabulaire (par rapport à la figure précédente) :

• (transdisciplinaire) système (N1?,N2, N3 et N4) ?
  = (en probabilité) expérience ? (de N1 à N4 ?)
  =

• (transdisciplinaire) macroétat (N1?,N2?, N3 et N4) ?
  = (en probabilité) résultat (N1 à N4) ?
  

• (transdisciplinaire) microétat (N1?,N2?, N3 et N4) ?
  = (en probabilité) ???
  

• (transdisciplinaire) paramètres (N1?,N2, N3 et N4) ?
  = (en physique classique) :
  coordonnées généralisées dans l'espace des phases (avec n=6) ?
  = (en mécanique hamiltonienne, N4) n moments conjugués ?
  = (en physique quantique, N3?-N4)