courses/12.temporary_ins/65.geometrical-optics/50.simple-elements/10.dioptre/20.overview/cheatsheet.fr.md

title	media_order	published	routable	visible
Le dioptre sphérique, en approximation paraxiale : synthèse	dioptre1ok.png,dioptre2ok.png,dioptre3ok.png,dioptre4ok.png	false	false	false

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

Très imparfait ... à reconcevoir intégralement ...

---

Qu'est-ce qu'un dioptre ?

Interface réfractante : description physique

• Interface séparant deux milieux transparents d'indices de réfraction différents..

• peut être trouvée dans la nature :
  Exemples :
  - une interface réfractante plane : la surface plane d'un lac tranquille. - une interface réfractante sphérique : un aquarium boule.

Fig. 1. L'interface réfranctante sphérique d'un aquarium boule.

• **apparaît dans la conception et modélisation de composants optiques ** :
  Exemples :
  - une vitre en verre se décompose en deux interface réfractantes planes (air/verre, puis verre/air), séparées par l'épaisseur de la vitre.
  - une lentille est la succession de deux interfaces réfractantes courbes (souvent sphériques) consécutives (air/verre, puis verre/air) qui présentent toutes deux une symétrie de révolution autour d'un même axe.

Interface réfractante versus surface réfractante

!!!! POINT DIFFICILE : une interface réfractante plane ou sphérique présente deux comportements optiques différents pour la formation d'image, est caractérisée par deux ensembles de paramètres de veleurs différentes, selon que la lumière considérée traverse l'interface dans un sens ou dans l'autre. !!!! !!!!Considère une interface plane (une vitre épaisse dont l'épaisseur et donc l'effet optique peuvent être négligés) séparant de l'air et de l'eau, et deux jumeaux (Thompson and Thomson) à égales distances de chaque côté de l'interface (Fig. 2a). !!!! !!!!
!!!! Fig. 2a : La situation n'est pas symétrique. !!!! !!!! * Quand Thompson (dans l'ir) regarde Thomson (dans l'eau), la lumière se propage de Thomson vers les yeux de Thompson. !!!! Le fait est que Thompson voit l'image de son frère plus proche que la position réelle de ce son frère (Fig. 2b) !!!! !!!!
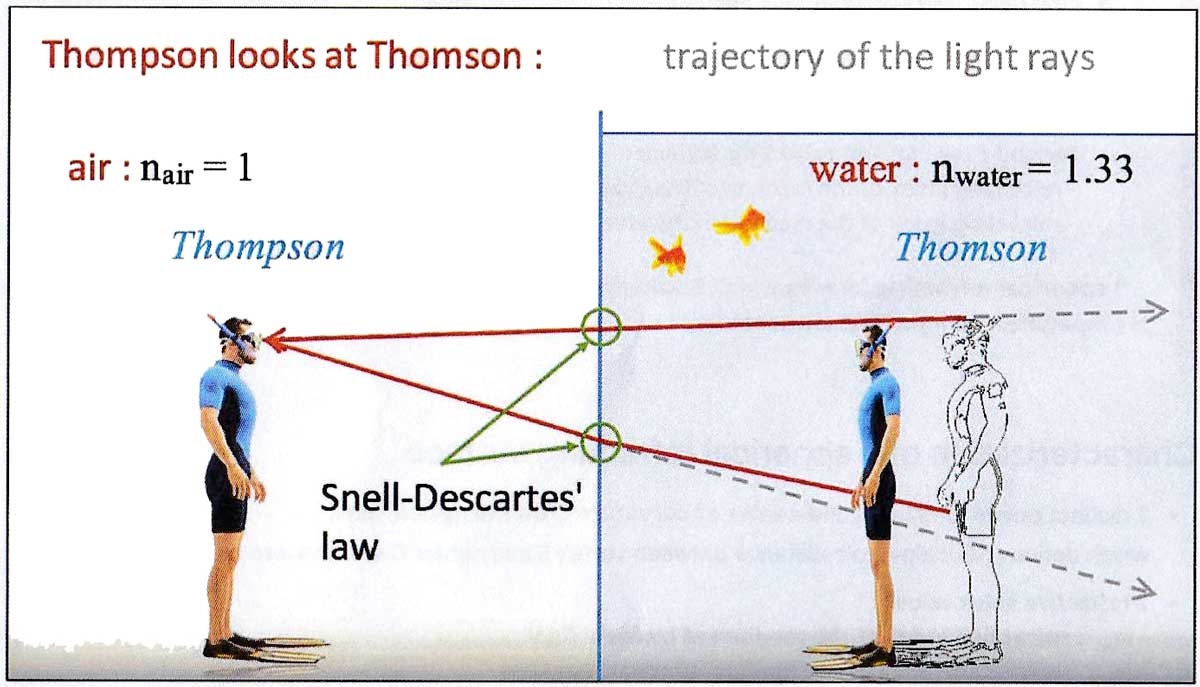
!!!! Fig. 2b. Thompson voit son frère plus proche que sa position réelle dans l'eau. !!!! !!!! * Dans la situation opposée, quand Thomson (dans l'eau) regarde Thompson (dans l'air), la lumière se propage de Thompson jusqu'aux yeux de Thomson. Et le fait est que Thomson voit l'image de son frère plus loin que sa position réelle (Fig. 2c)
!!!! (en toute rigueur, les yeux d'un poisson devraient être considérés dans cet exemple, des yeux plus adaptés à la vision sous-marine et des yeux en contact direct avec l'eau. Sinon, nous devrions considérer que le masque de plongée de Thompson est rempli d'eau pour ne pas ajouter déjà une autre interface eau/air (celle du masque de plongé) sur la trajectoire de la lumière). !!!! !!!!
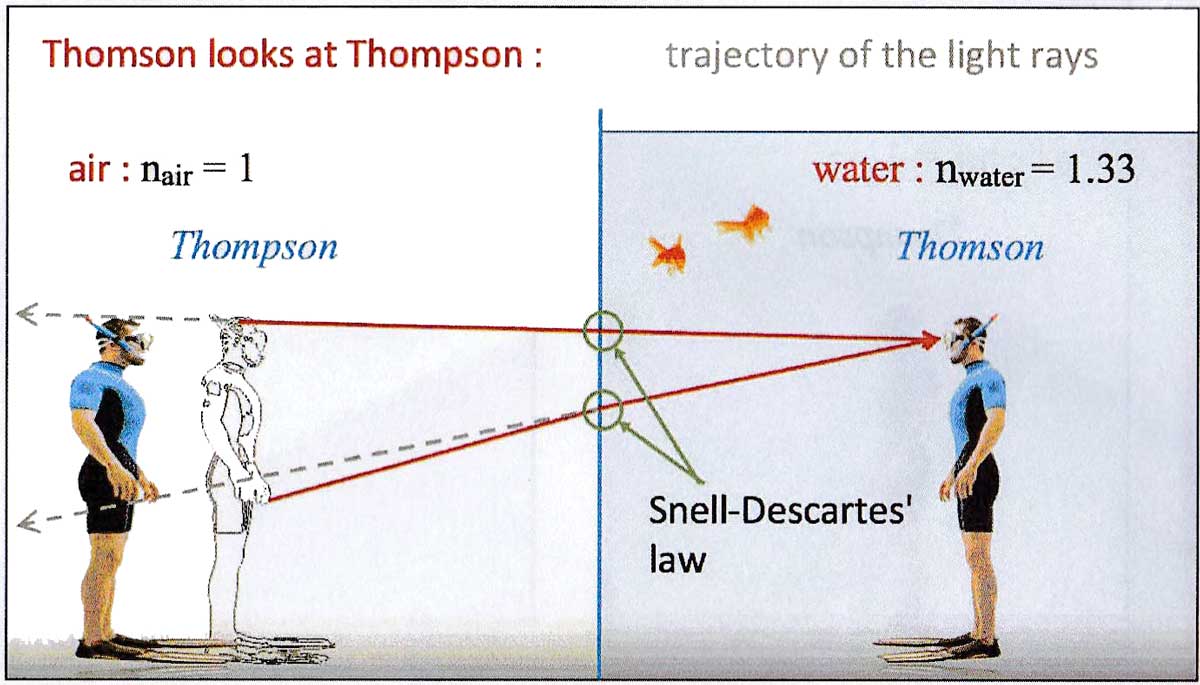
!!!! Fig. 2c. Thomson voit son frère plus loin que sa position réelle dans l'air. !!!! !!!! Tout ceci peut être calculé et prédit, mais cet exemple montre que cette interface réfratante plane air/eau correspond à deux surface réfrantantes:
!!!! !!!! * Premier cas, la surface réfractante est telle que :
!!!! - indice de réfraction de milieu de la lumière incidente : $n_{inc} = n_{water} = 1.33$
!!!! - indice de réfraction de milieu de la lumière émergente : $n_{eme} = n_{air} = 1$
!!!! !!!! *¨ Deuxième cas, la surface réfractante est telle que :
!!!! - indice de réfraction de milieu de la lumière incidente : $n_{inc} = n_{air} = 1$
!!!! - indice de réfraction de milieu de la lumière émergente : $n_{eme} = n_{water} = 1.33$. !!!!

Dioptre

Un dioptre est une surface réfractante dont un sens de propagation de la lumière est précisé.

Différence de terminologie entre l'espagnol, le français et l'anglais.

!!!! ATTENTION :
!!!! De la même façon qu'en français est utilisé le simple mot "miroir" pour nommer une "surface réfléchissante", le simple mot !!!! "dioptre" définit une "surface réfractante". Cela n'est pas le cas en espagnol et en anglais. Un "dioptre" sera traduit par !!!! "superficie refractiva" en espagnol, et "refracting surface" en anglais. !!!! !!!! Le mot "dioptre" en anglais et son équivalent espagnol "dioptría" désignent l'unité de mesure de la vergence d'un système optique. En français, cette unité !!!! de mesure se nomme "dioptrie". !!!! Donc, garde à l'esprit le schéma suivant : !!!! !!!! surface réfractante : EN : refracting surface , ES : superficie refractiva , FR : dioptre.
!!!! Une boule de cristal forme un dioptre sphérique : une superficie refractiva esférica en espagnol, a spherical !!!! refracting surface en anglais. !!!! !!!! unité de mesure : EN : dioptre , ES : dioptría , FR : dioptrie.
!!!! _mon verre correcteur pour ma myopie fait -4 dioptries : "-4 dioptrías" en espagnol et "-4 dioptres" en anglais.

Non stigmatisme du dioptre sphérique

Etude au tracé de rayons d'un dioptre sphérique :

• En tout point d'impact des rayons sur le dioptre sphérique, la relation de Snell-Descartes s"applique.

• Un dioptre sphérique est non stigmatique : Les rayons (ou leurs prolongements) provenant d'un même point objet et qui émergent du dioptre, en général ne convergent pas en un point image.

• Si l'ouverture du dioptre sphérique est limité de façon que seuls les rayons interceptant le dioptre proche de son sommet soient réfractés par le dioptre,

• et si les points object restent situés suffisamment proches de l'axe optique, de façon que les angles d'incidence et de réfraction restent petits, alors pour chaque point objet un point image peut presque être défini, et dès lors le dioptre sphérique devient quasi-stigmatique.

Conditions de Gauss / approximation paraxiale et stigmatisme approché.

Quand un dioptre sphérique est utilisé dans les conditions suivantes, nommées conditions de Gauss :
- les angles d'incidence et de réfraction sont faibles
(rayons faiblement inclinés sur l'axe optique quiinterceptent le dioptre au voisinage de son sommet),
alors le dioptre sphérique peut être considéré comme quasi-stigmatique, et dès lors il peut être utilisé pour construiire des images.

Mathematiquement, quand un angle $\alpha$ est suffisamment petit $\alpha < ou \approx 10^\circ$, les approximations suivantes peuvent être faites made :
$sin(\alpha) \approx tg(\alpha) \approx \alpha (rad)$, and $cos(\alpha) \approx 1$.

*L'optique géométrique restreinte aux conditions de Gauss s'appelle l'optique gaussienne ou l'optique paraxiale.

Dioptre sphérique mince

Nous appellerons dioptre sphréique mince un dioptre sphérique utilisé dans les conditions de Gauss.

Comment est modélisé un dioptre sphérique mince en optique paraxiale ?

Caractérisation d'un dioptre sphérique

• 2 points distincts : sommet S et centre de courbure C sur l'axe optique, qui définisent $\overline{SC}$ : distance algébrique entre le sommet S et le centre de courbure C sur l'axe optique.

• 2 valeurs d'indices de réfraction :
  - $n_{inc}$ : indice de réfraction du milieu de propagation de la lumière incidente.
  - $n_{eme}$ : indice de réfraction du milieu de propagation de la lumière émergente.

• 1 flèche : indique le sens de propagation de la lumière

Etude analytique

• Equation de conjugaison du dioptre sphérique mince
  
  $\dfrac{n_{eme}}{\overline{SA_{ima}}}-\dfrac{n_{inc}}{\overline{SA_{obj}}}=\dfrac{n_{eme}-n_{inc}}{\overline{SC}}$   (equ.1)

• Expression du grandissement transversal
  
  $\overline{M_T}=\dfrac{n_{inc}\cdot\overline{SA_{ima}}}{n_{eme}\cdot\overline{SA_{obj}}}$    (equ.2)
  
  Tu connais $\overline{SA_{obj}}$, $n_{inc}$ et $n_{eme}$, tu as précédemment calculé $\overline{SA_{ima}}$, alors tu peux calculer $\overline{M_T}$ et en déduire $\overline{A_{ima}B_{ima}}$.

! UTILE : L'équation de conjugaison et l'expression du grandissement transversal pour un dioptre plan !s'obtiennent et se retrouvent à partir de celles du dioptre sphérique dans la limite ! ! $|\overline{SC}|\longrightarrow\infty$.
! alors tu obtiens pour un dioptre plan : ! ! * équation de conjugaison :   $\dfrac{n_{fin}}{\overline{SA_{ima}}}-\dfrac{n_{ini}}{\overline{SA_{obj}}}=0$    (equ.3) ! ! * expression du grandissement transverse :   $\dfrac{n_{ini}\cdot\overline{SA_{ima}}}{n_{fin}\cdot\overline{SA_{obj}}}$    (equ.2, unchanged)

! mpais (equ.3) donne $\dfrac{\overline{SA_{ima}}}{\overline{SA_{obj}}}=\dfrac{n_{inc}}{n_{eme}}$.
! Copier ce résultat dans (equ.2) conduit à $\overline{M_T}=+1$.

Etude graphique

1 - Déterminer les points focaux objet et image

Les positions des points focaux objet F et image F’s'obtiennent facilement à partir de l'équation de conjugaison (equ. 1).

• Distance focale image $\overline{OF'}$ : $\left(|\overline{OA_{obj}}|\rightarrow\infty\Rightarrow A_{ima}=F'\right)$
      (equ.1)$\Longrightarrow\dfrac{n_{eme}}{\overline{SF'}}=\dfrac{n_{eme}-n_{inc}}{\overline{SC}}$ $\Longrightarrow\overline{SF'}=\dfrac{n_{eme}\cdot\overline{SC}}{n_{eme}-n_{inc}}$   (equ.4)

• Distance focale objet $\overline{OF}$ : $\left(|\overline{OA_{ima}}|\rightarrow\infty\Rightarrow A_{obj}=F\right)$
      (equ.1) $\Longrightarrow-\dfrac{n_{inc}}{\overline{SF}}=\dfrac{n_{eme}-n_{inc}}{\overline{SC}}$ $\Longrightarrow\overline{SF}=-\dfrac{n_{inc}\cdot\overline{SC}}{n_{eme}-n_{inc}}$   (equ.5)

!!!! CONSEIL :
!!!! La mémoire ne remplace pas la compréhension. Ne mémorise pas (equ.4) and (equ.5), mais comprends !!!! les définitions des points focaux objet et image, et comment reyrouver ces deux équations !!! à partir de l'équation de conjugaison d'un dioptre sphérique. !!!!

! REMARQUE 1 :
! Un élément optique est convergent quand son point focal image est réel, ! soit quand $\overline{OF}>0$ (avec l'axe optique orienté positivement dans le sens de propagation de la lumière), ! Donc tu peux déduire en observant (equ.4) qu'un dioptre sphérique est convergent si et seulement si son centre ! de courbure C se trouve situé dans le milieu de plus fort indice de réfraction. !

2 - Représentation d'un dioptre sphérique mince

• Axe optique = axe de révolution du dioptre, orienté positivement dans le sens de propagation de la lumière.

• représentation d'un dioptre sphérique mince :
  
  - sègment de droite, perpendiculaire à l'axe optique, centré sur cet axes avec indication symbolique de la concavité ou de la convexité du dioptre aux extrémités du sègment.
  
  - sommet S, qui localise le dioptre sur l'axe optique.
  
  - point nodal C = centre de courbure.
  
  - points focaux objet F et image F’.

! REMARQUE 2
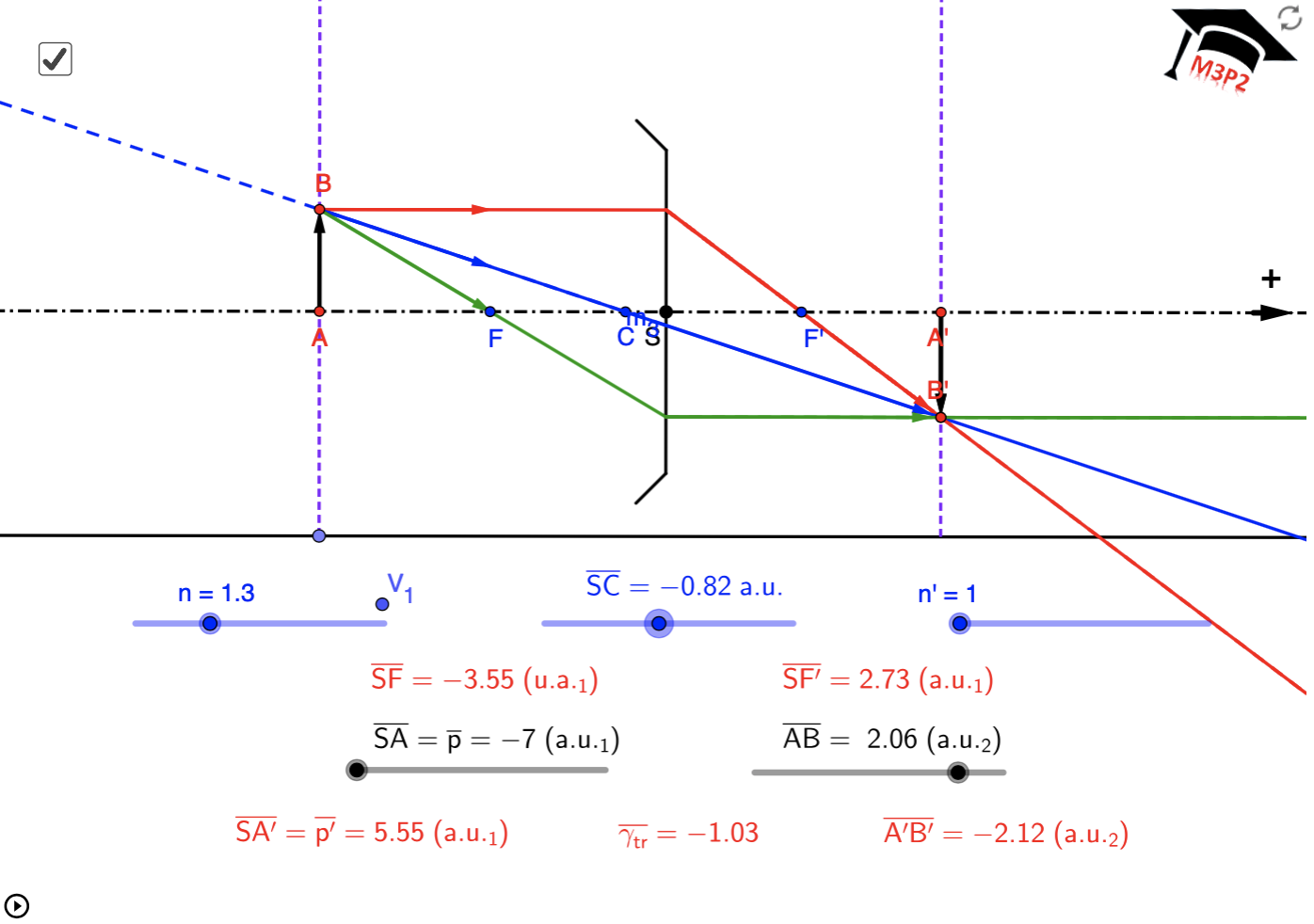
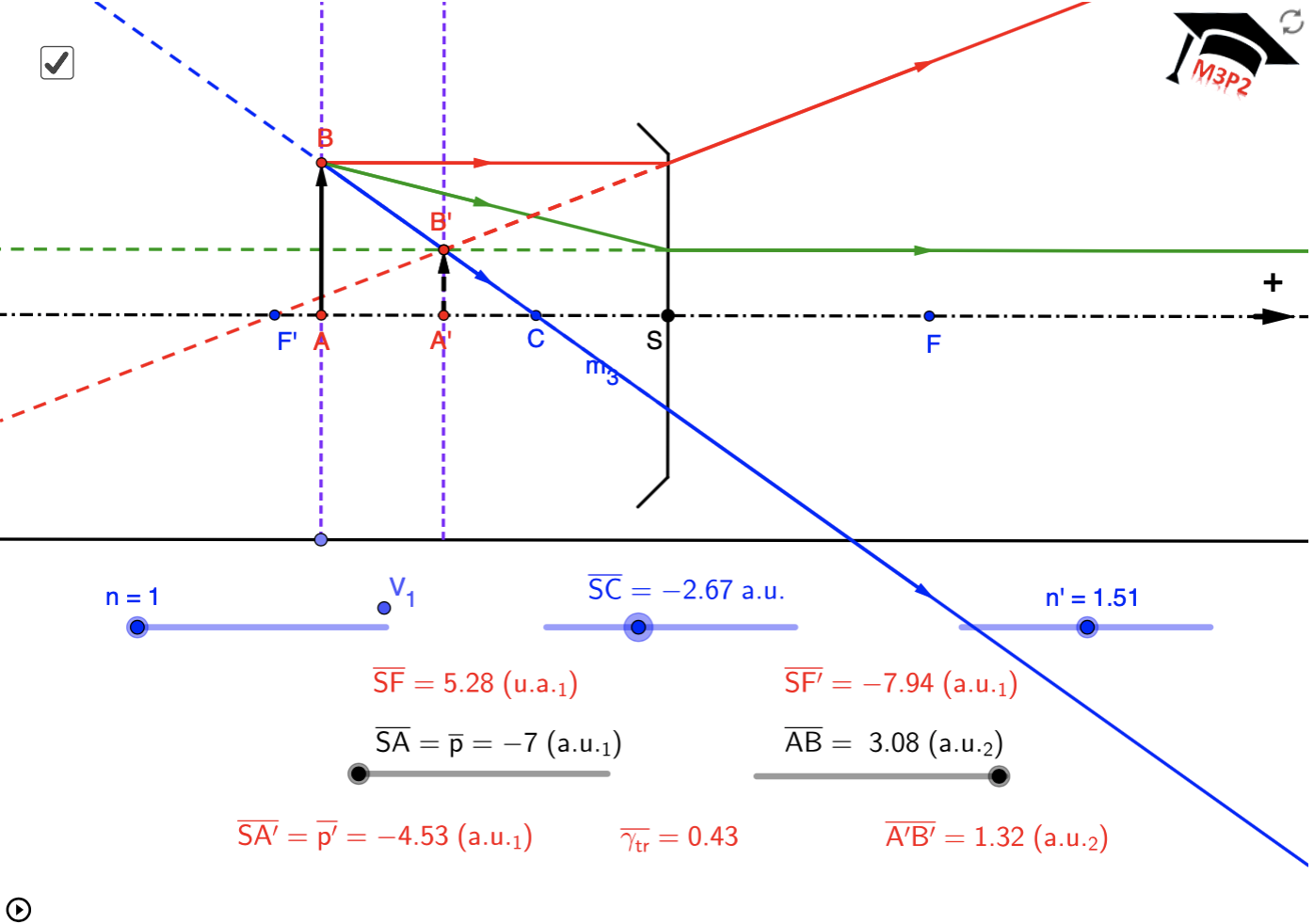
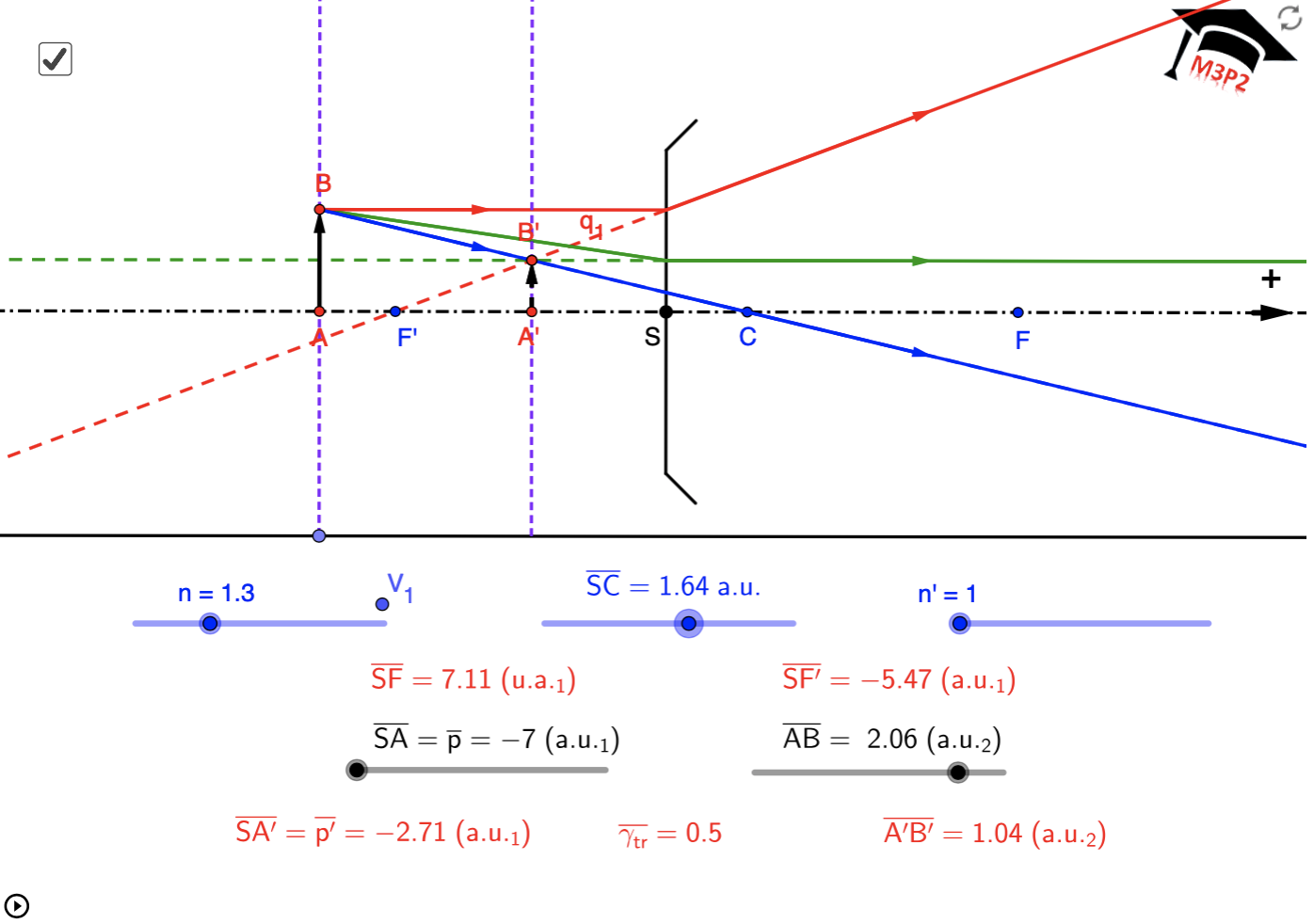
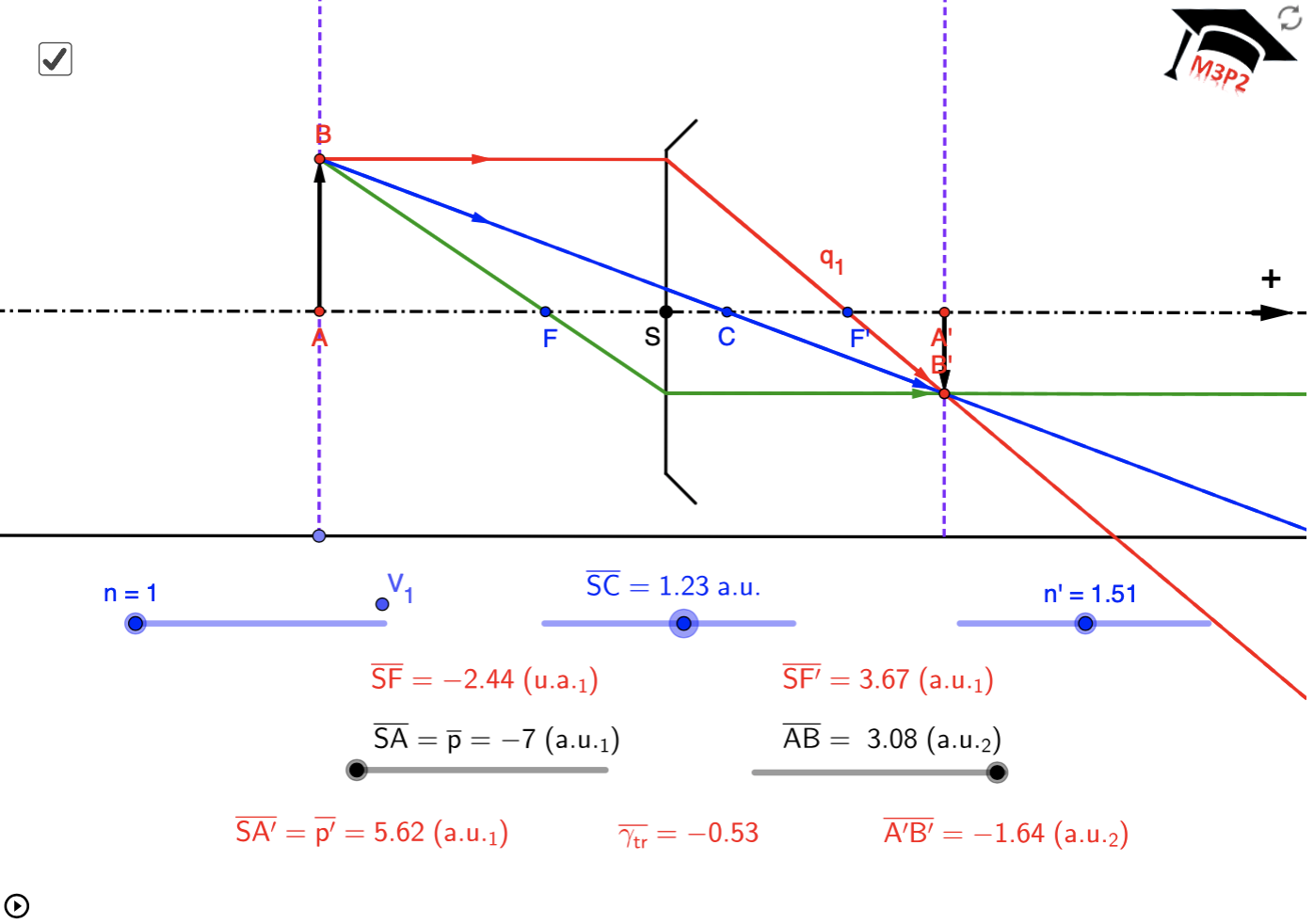
! La concavité d'un dioptre ne présume pas de son caractère convergent ou divergent. Cela dépend aussi ! des valeurs des indices de réfraction de chaque côté du dioptre. Pour illustrer cela, regarde ce qui se passe pour le rayon incident parallèle à l'axe optique sur les figures 3 et 4, puis 5 et 6 ci-dessous, et relis la REMARQUE 1. !

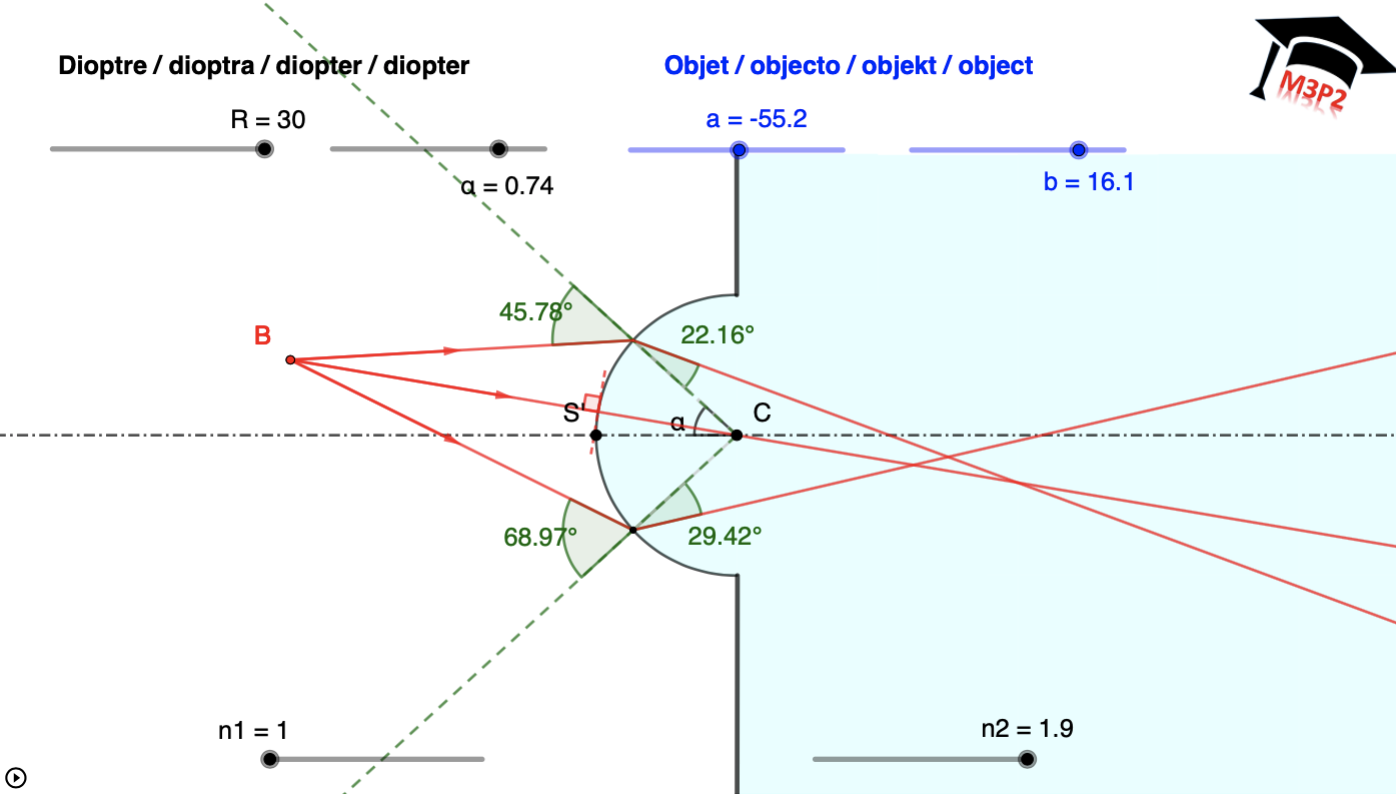
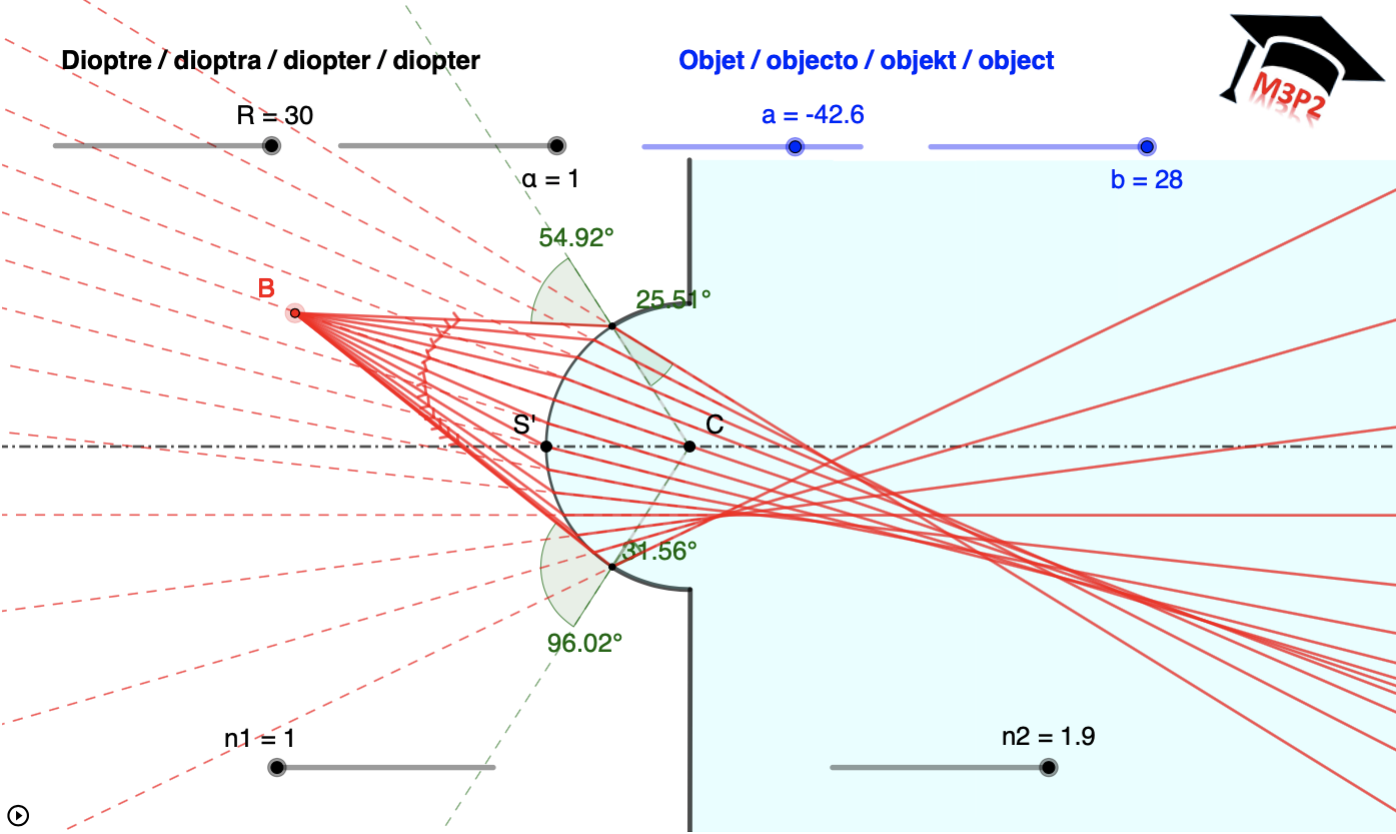
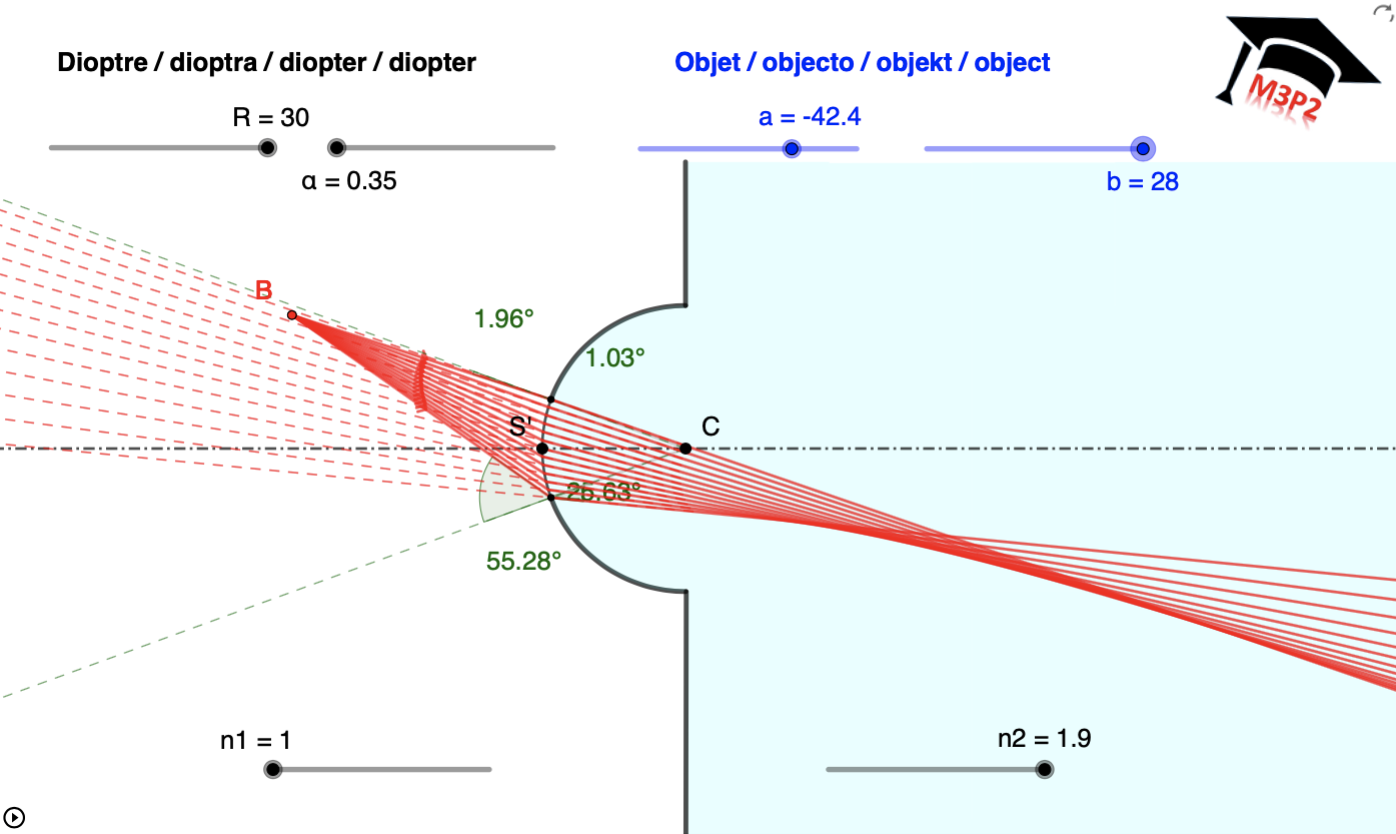
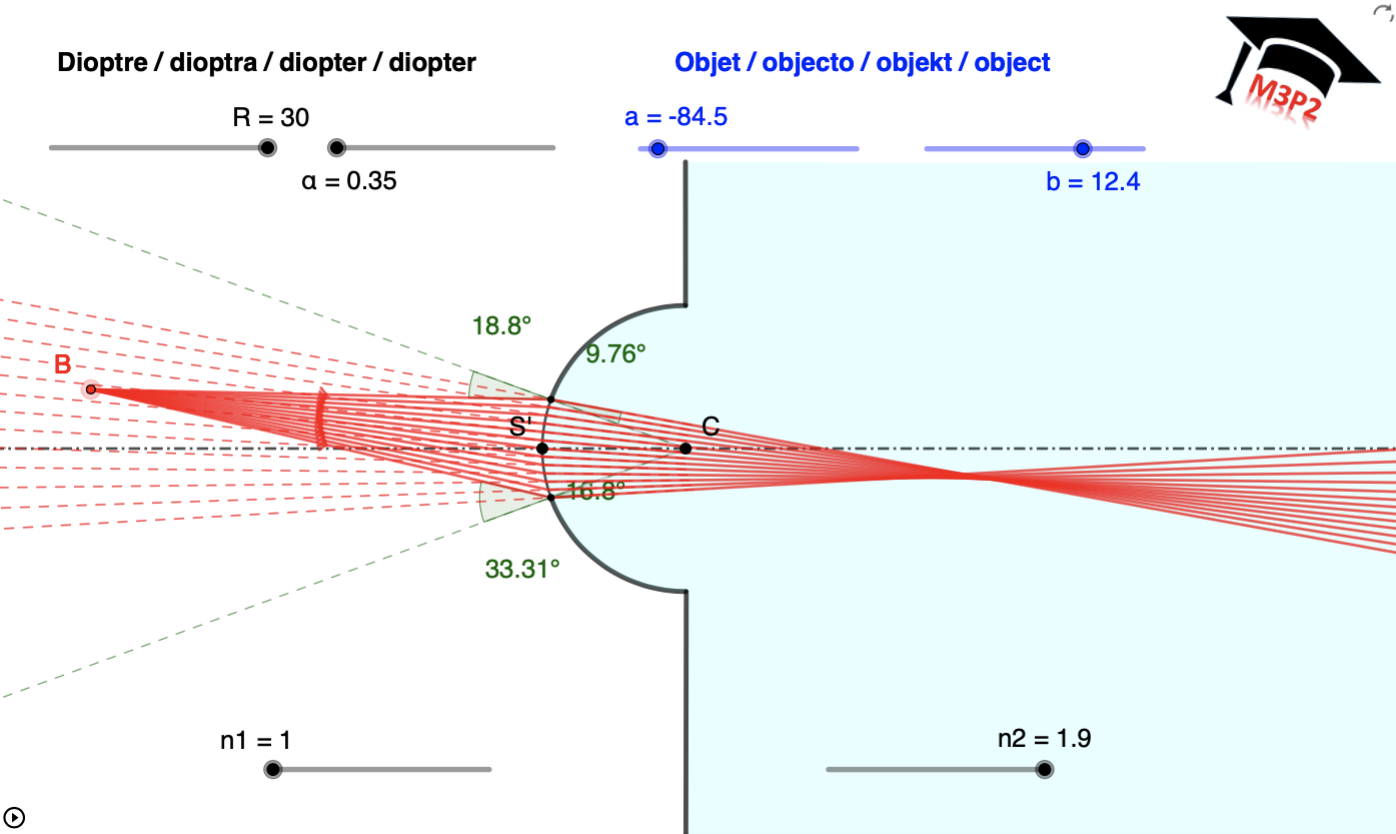
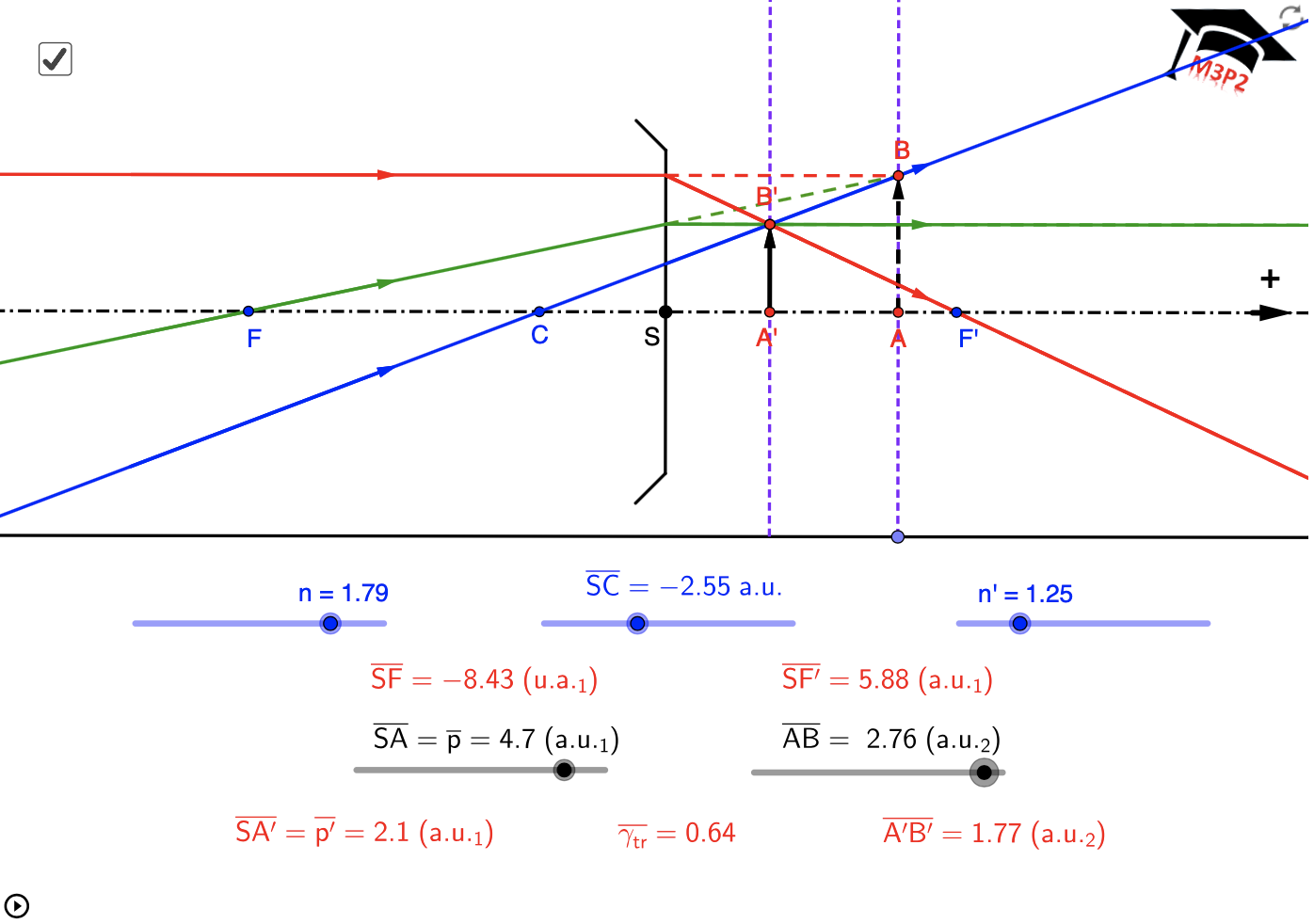
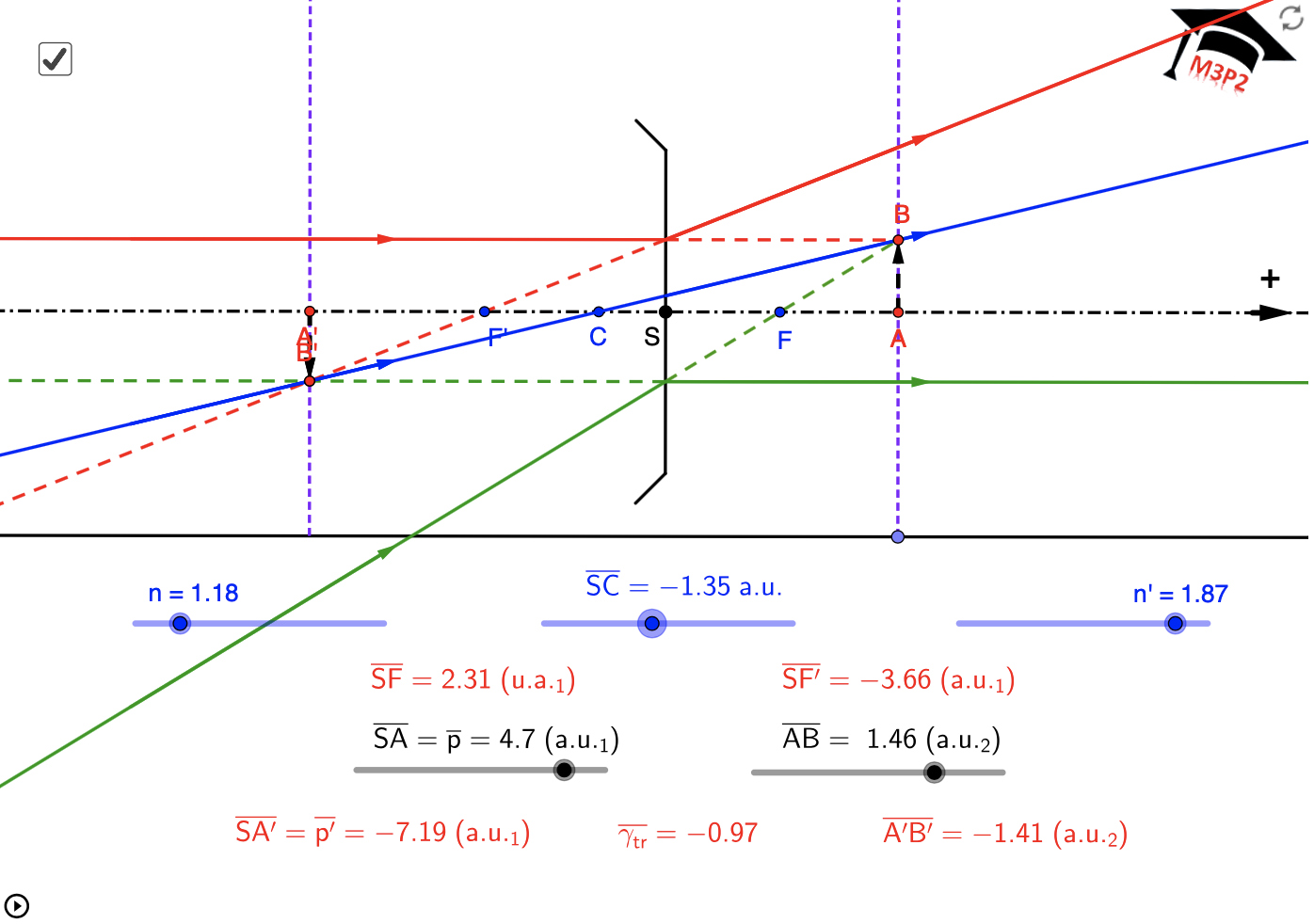
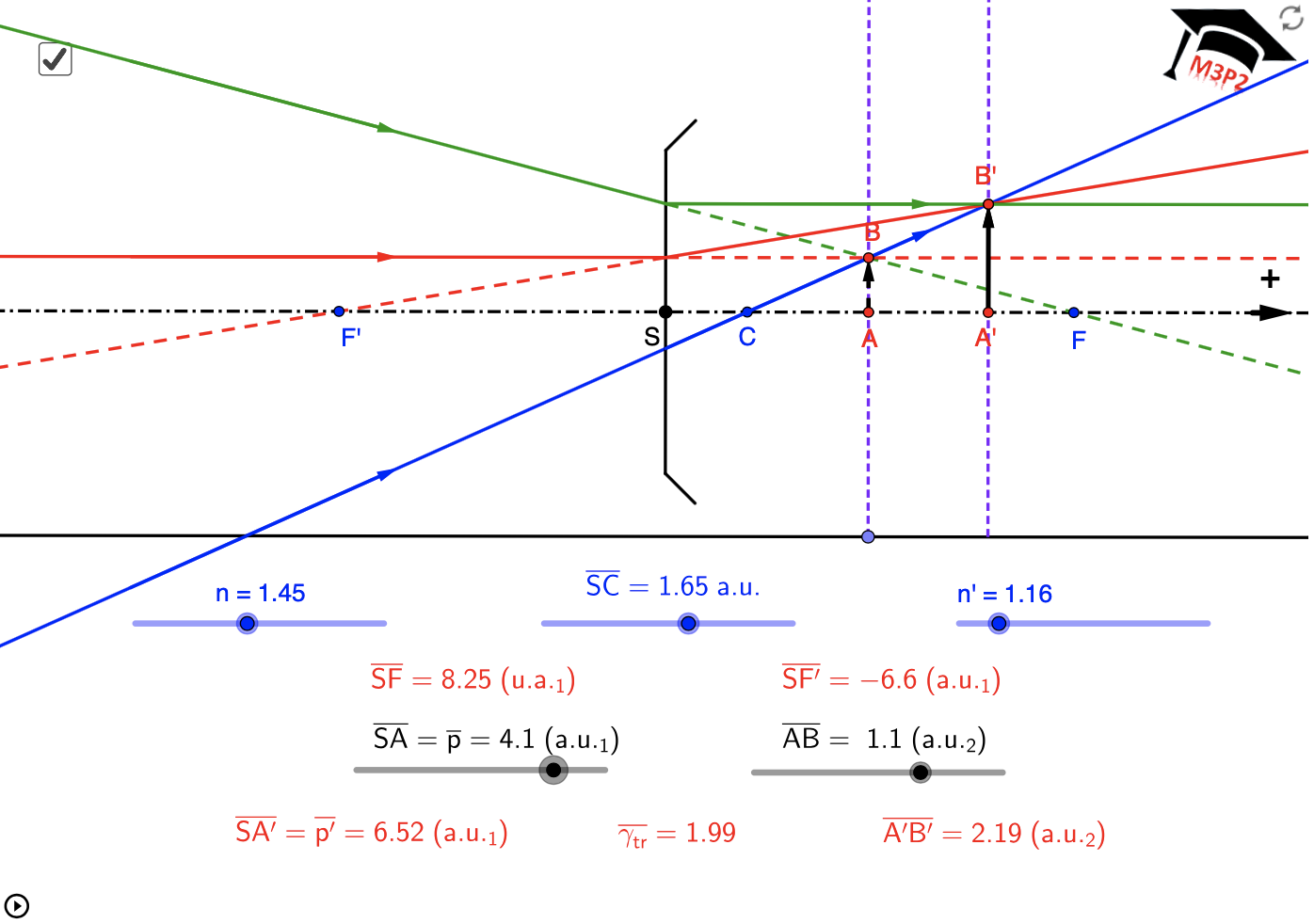
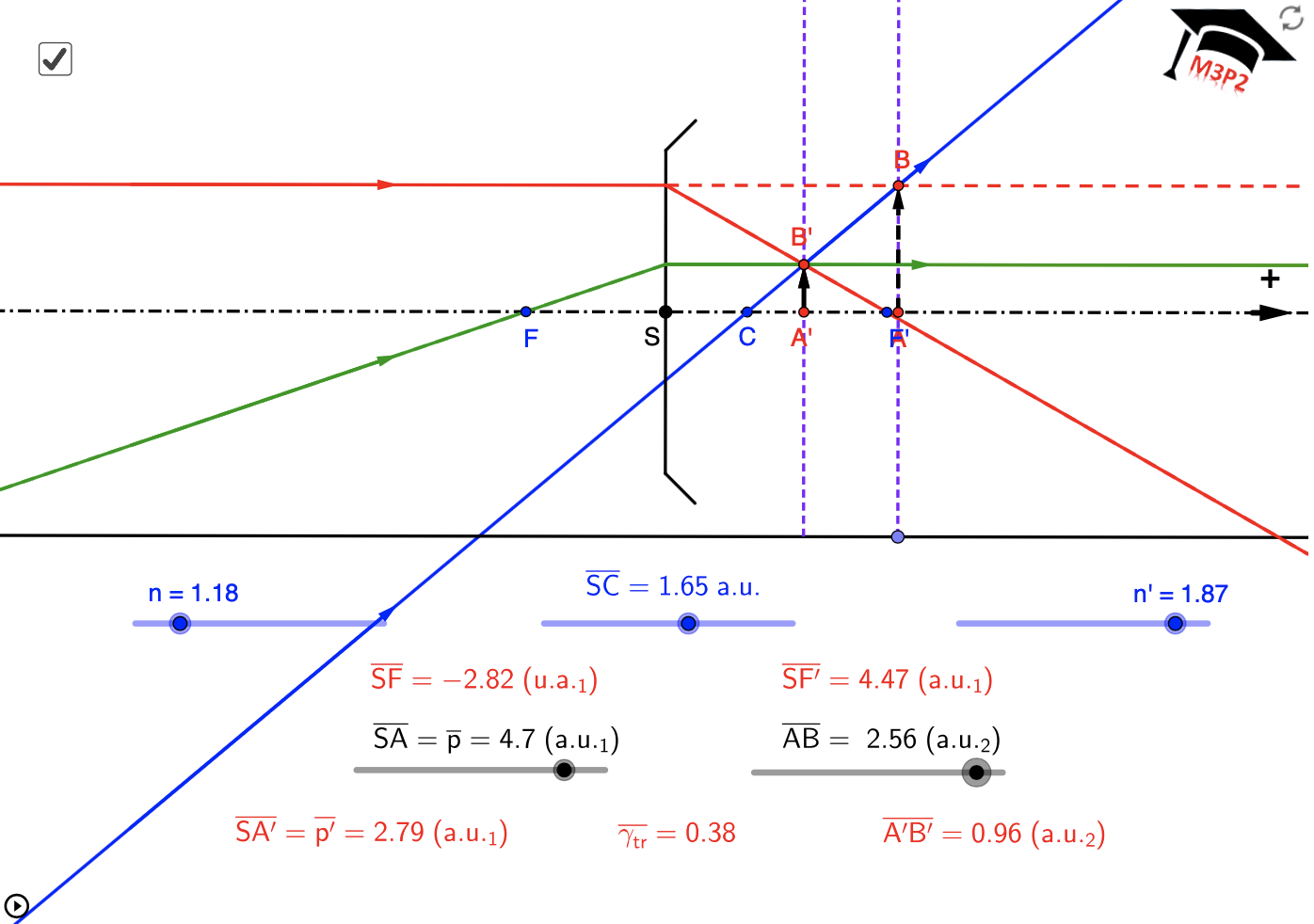
Exemples de situations graphiques, avec valeurs numériques affichées pour t'entraîner

!!!! IMPORTANT :
!!!! Même en considérant une seule de ces figures, le caractère réel ou virtuel de l'image !!!! peut dépendre de la position de l'objet. Ce paragraphe est seulement pour t'aider à comprendre !!!! comment placer les 3 rayons particuliers qui permettent de déterminer l'image. Il est important !!!! de ne pas mémoriser ces figures, cela serait limitatif, trompeur et sans intérêt. !!!! !!!! Toutes les valeurs numériques utiles sont associées à chaque figure, tu peux vérifier que tu maîtrises !!!! aussi le calcul analytique permettant de localiser l'image dans chaque cas. !!!!

• avec objets réels

Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7.

• avec objets virtuels

Fig. 8.

Fig. 9.

Fig. 10.

Fig. 11.