courses/12.temporary_ins/15.electrokinetics/20.overview/cheatsheet.fr.md

title	published	routable	visible
Electrocinétique	true	true	false

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

Vraiment pas au point. A revoir et réorganiser un minimum... Il manque aussi un signe moins dans l'équation de la figure current-intensity-definition-2_v1_L1200, lorsque I>0...

Qu'est-ce qu'un milieu conducteur électrique ?

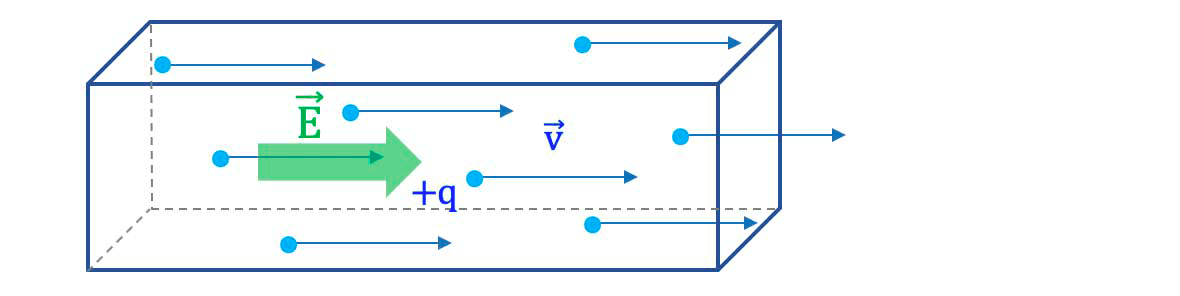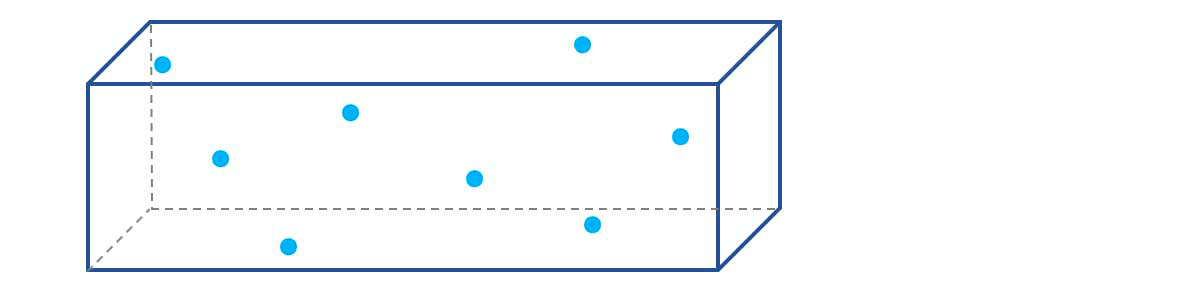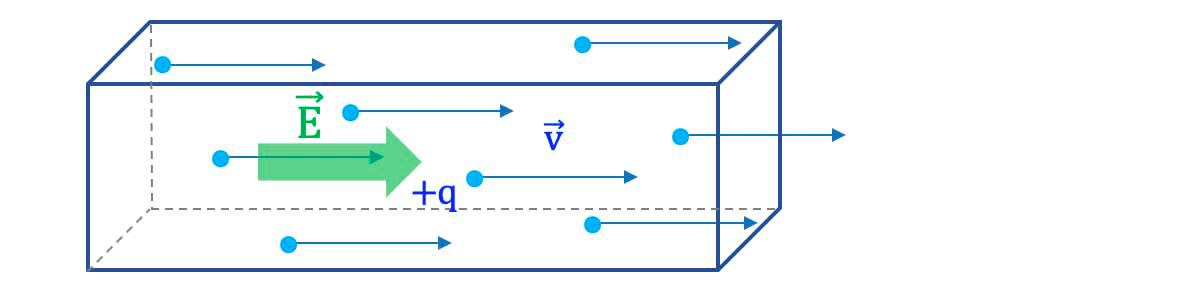
Un milieu est électriquement conducteur si il contient des charges libres de se déplacer à travers le milieu sous l'influence d'un champ électrique aussi faible soit-il.

• Dans les conducteurs solides, les charges libres sont des électrons.
• Dans les conducteurs liquides (électrolytes), les charges libres sont des ions positifs et des ions négatifs.
• Dans les conducteurs gazeux (plasma), les porteurs de charges sont des électrons et des ions positifs.

Qu'est-ce qu'un courant électrique ?

Courant électrique, et intensité du courant électrique

• Courant électrique : tout mouvement de porteurs de charge électrique.

• Intensité $I$ du courant électrique :
  

  • L'intensité $I$ d'un courant électrique quantifie la charge électrique qui traverse une surface donnée par unité de temps.
  • Si une charge $\Delta Q$ traverse une surface $S$ entre les instants $t-\Delta t$ et $t$, $t$ étant un instant quelconque, alors l'intensité du courant électrique à traverse la surface $S$ à l'instant $t$ s'exprime comme la rapport de la charge électrique $\Delta Q$ par l'intervalle de temps $\Delta t$ :
    
    $\mathbf{I=\left. \dfrac{\Delta Q}{\Delta t} \right|_S}$
    

• Unité SI de l'intensité $I$ : Ampère, de symbole $A$.
  
  Un courant d'intensité d'un ampère ($1\,A$) en valeur absolue correspond à une charge électrique qui traverse une surface donnée à un taux de 1 Coulomb ($1\,C$) par seconde ($1\,s$).
  
  $\mathbf{I=\,1\,A\quad\Longleftrightarrow\quad I=\left. \dfrac{\Delta Q}{\Delta t} \right|_S=\left. \dfrac{1\,C}{1\, s}\right|_S}$

! Note :
! L'Ampère est une unité de base du système international d'unités parmi les sept unités de base qu'il contient et qui sont le mètre, le kilogramme, la seconde, l'ampère, le kelvin, la mole et la candela.
! Toutes les autres unités, nommées unités dérivées, s'expriment en fonction des sept unités de base à partir d'une analyse dimensionnel.

Valeur absolue et valeur algébrique de l'intensité

• Pour une surface donnée (d'aire) $S$, la charge électrique qui la traverse peut être positive ou négative, et elle peut traverser la surface dans un sens ou dans l'autre. Ces différentes possibilités sont quantifiées par une valeur de l'intensité qui peut être positive ou négative.

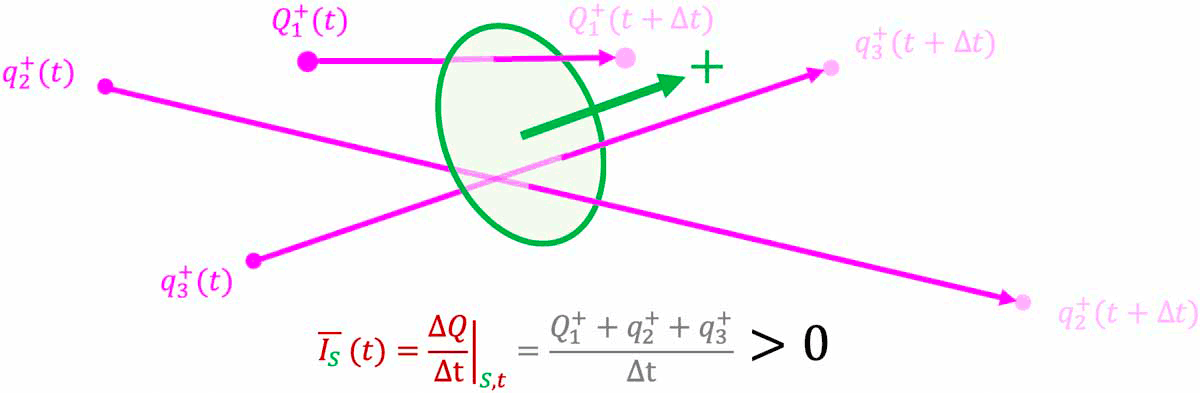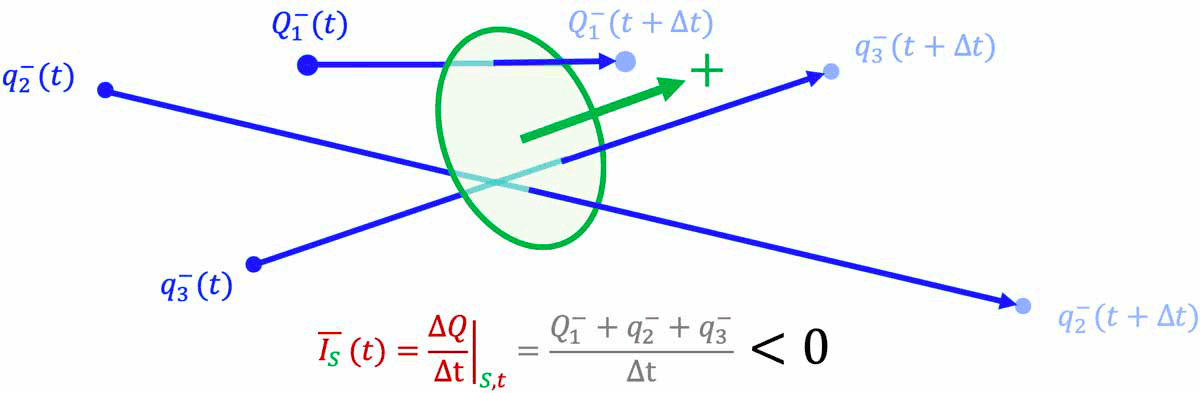
• Par définition, l'intensité $I$ en valeur algébrique du courant électrique à travers une surface orientée $S$ est égale à la charge électrique $\Delta Q$ qui traverse cette surface $S$ dans le sens positif de la surface pendant la durée $\Delta t$.
  

• En toute rigueur, il faudrait noter $\overline{I}$ l'intensité exprimée en valeur algébrique.

!!! * Pour une surface fermée (ce qui signifie qu'elle délimite un volume, et qu'elle permet donc de définir un intérieur et un extérieur à ce volume) le sens du courant est le sens de déplacement d'une charge positive qui traverse par unité de temps la surface de l'intérieur vers l'extérieur (ou, équivalent, d'une charge nagétive qui traverse par unité de temps la surface de l'extérieur vers l'intérieur). !!!! !!!! * Pour une surface ouverte, les notions d'intérieur et d'extérieur ne peuvent être définie par la surface. Un sens positif de traversée de la surface doit alors être choisi arbitrairement. Le sens du courant est alors le sens de déplacement d'une charge positive qui traverse par unité de temps la surface dans son sens positif (ou, équivalent, d'une charge nagétive qui traverse par unité de temps la surface dans son sens négatif).

• Le signe de l'intensité $I$ d'un courant électrique en notation algébrique dépend du signe de la charge électrique qui traverse la surface $S$ dans son sens positif.

• Le signe de l'intensité $I$ d'un courant électrique en notation algébrique à travers une surface ouverte $S$ dépend du sens positif choisi *pour cette surface.

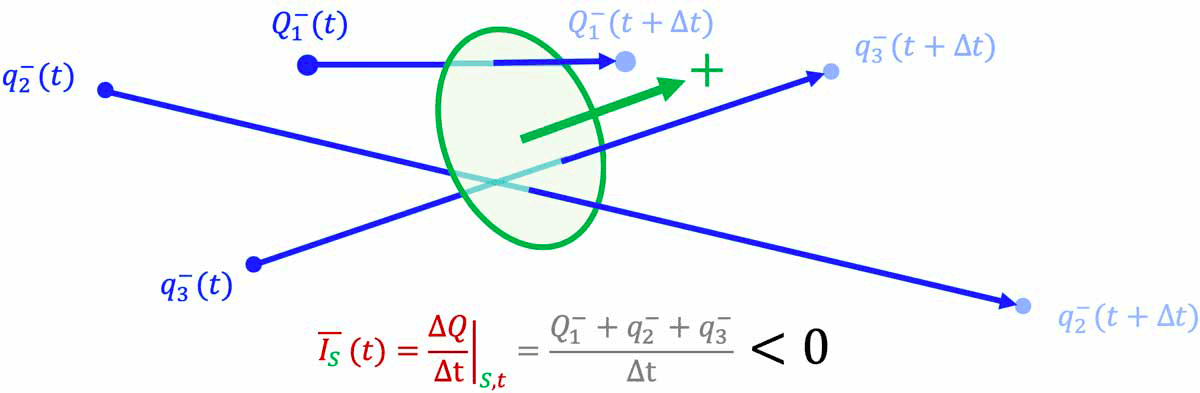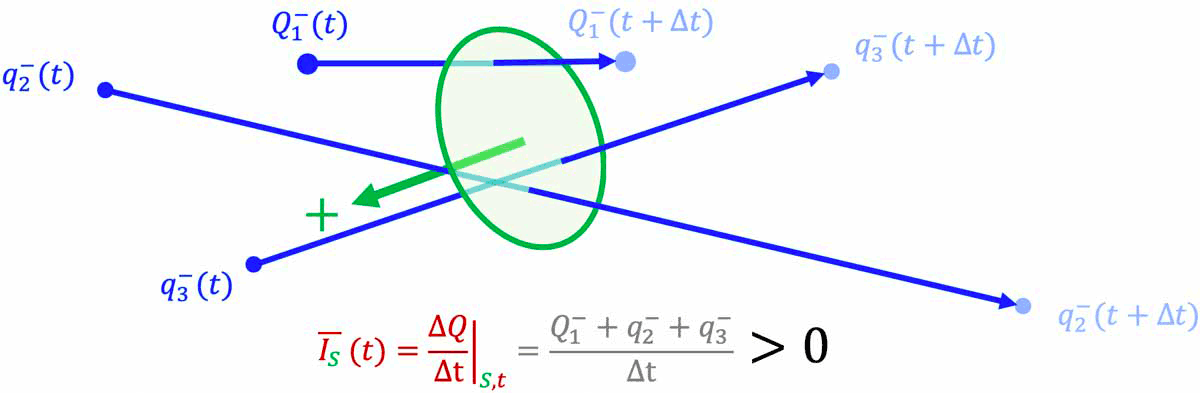
Attention : Il faut corriger le signe des charges sur l'une des deux images du gif.

• L'expression de l'intensité en valeur absolue peut être utilisé lorsque l'effet de ce courant auquel nous nous intéressons ne dépend pas du sens du courant électrique.
  C'est le cas lorsque nous intéressons à l'effet Joule, qui permet de connaître la puissance dissipée du courant dans une résistance.

• L'expression de l'intensité en valeur algébrique est nécessaire lorsque l'effet de ce courant dépend du sens du courant électrique. C'est en particulier le cas lorsque :
  

  • le circuit comprend une diode.
  • on s'intéresse aux effets electromagnétiques induits par les courants.

Intensité de $1\,A$ et nombre de porteurs de charge

• Dans le cas le plus général, les intensités de courants électriques correspondants à des mêmes charges traversant deux surfaces d'aires différentes peuvent être égales. Cependant, cette possibilité théoriquement possible ne peut exister que pour des surfaces et des densités volumiques de charges extrêmement petites.

• Dans les matériaux conducteurs solides, les charges libres de se déplacer sont des électrons. Un électron porte une charge négative $q_e=-1,6\cdot e^{-19}\,C$. Ainsi, une surface $S$ traversée par un courant infime d'intensité $I=1\,nA=10^{-9}\,A$ est une surface déjà traversée chaque seconde par le nombre considérable de $n=...$.

• Lorsque la surface à travers laquelle est mesurée l'intensité d'un courant électrique est traversée par un très grand nombre de porteurs de charge individuels, et que leurs trajectoires traversent la surface en des points distribués de façon homogène sur toute la surface, alors aux fluctuations statistiques près :
  

  1. L'intensité du courant électrique est proportionnel à la surface à travers laquelle il est évalué.
  2. L'intensité dépend de l'inclinaison entre la surface traversée et la direction moyenne des trajectoires des porteurs.

(manque une ou deux des images précédentes, en remplaçant les 3 charges ponctuelles par un nuage de point... à mettre au point).

Quelle différence entre intensité instantanée et intensité moyenne ?

• Par définition, l'intensité du courant électrique à l'instant $t$ est la charge électrique $\Delta Q$ qui traverse une surface $S$ donnée entre les instants $t-\Delta t$ et $t$, divisé par l'intervalle de temps $\Delta t$.
  
  $I=\left. \dfrac{\Delta Q}{\Delta t} \right|_S$

• L'intensité instantanée $I(t)$ correspond au cas où l'intervalle de temps ne peut être résolu, c'est à dire que $\Delta t$ est le plus petit intervalle de temps discernable par l'appareil de mesure de l'intensité. C'est le cas où $\Delta t$ apparaît comme ponctuel sur l'axe du temps, et cela se traduit mathématiquement par le fait que $\Delta t$ tend vers zéro, et s'écrit $dt$ :
  
  $\mathbf{I(t)=\left. \dfrac{dQ}{dt} \right|_S}$

• L'intensité moyenne $\langle\, I(t) \,\rangle_{\Delta t}$ mesurée, ou calculée ultérieurement, sur une période $\Delta t$ correspond au cas où l'intervalle de temps $\Delta t$ n'est pas la limite de résolution temporelle* de l'appareil de mesure. Dans ce cas, l'intensité moyenne est la charge $\Delta Q$ qui a traversé une surface donnée $S$ entre les instants $t-\Delta t$ et $t$, divisée par $\Delta t$ :
  
  **$\mathbf{\langle\, I(t) \,\rangle_{\Delta t} =\left. \dfrac{\Delta Q}{\Delta t} \right|_S}$**
  
  Comme $\Delta Q$ est l'intensité instantanée intégrée entre les instants $t-\Delta t$ et $t$,
  $\displaystyle\Delta Q=\int_{t-\Delta t}^{t} dq $$\quad=\int_{t-\Delta t}^{t} \dfrac{dq}{dt}\cdot dt = \int_{t-\Delta t}^{t} I(t)\cdot dt$,
  alors nous en déduisons :
  
  **$\displaystyle\mathbf{ \langle\, I(t) \,\rangle_{\Delta t} =\dfrac{1}{\Delta t}\int_{t-\Delta t}^{t} I(t)\cdot dt}$**
  
  ou, écriture beaucoup plus lisible, non?
  
  **$\displaystyle\mathbf{ \lt I(t) \gt_{\Delta t} =\dfrac{1}{\Delta t}\int_{t-\Delta t}^{t} I(t)\cdot dt}$**

Quelle différence entre intensité moyenne et intensité efficace ?

à faire

Quelles différences entre un courant stationnaire, variable, alternatif, périodique, et sinusoïdal ?

• Un courant est stationnaire, ou continu si son intensité instantanée $I(t)$ reste constante au cours du temps.

• Un courant est variable si son intensité instantanée $I(t)$ varie au cours du temps.

• Un courant alternatif est un courant variable dont le sens du mouvement d'ensemble des porteurs de charge s'inverse au cours du temps, donc si son intensité instantanée exprimée en valeur algébrique change de signe au cours du temps.

• Un courant périodique est un courant variable, alternatif ou non, si la variation temporelle $I(t)$ de son intensité peut se décomposer en la répétition jointive dans le temps d'un motif unique $I_P(t)$.
  La période $T$ du courant périodique est la durée de ce motif.

• Un courant sinusoïdal, ou harmonique est un courant alternatif dont l'intensité $I(t)$ est une fonction sinusoïdale du temps, d'écritures mathématiques :
  

  • $\mathbf{I(t)=I_0 \sin(\omega t + \varphi_0)}$
    avec :
    $\quad I(t)$ : intensité instantanée, d'unité SI $A$.
    $\quad I_0$ : amplitude de l'intensité, d'unité SI $A$.
    $\quad \omega$ : pulsation, d'unité SI $rad.s^{-1}$.
    $\quad \varphi(t)=\omega t + \varphi_0$ : phase du courant à l'instant $t$, d'unité SI $rad$.
    $\quad \varphi_0$ : phase à l'origine ($t=0$), d'unité SI $rad$.
    
    

  • ou $\mathbf{I(t)=I_0 \cos(\omega t + \varphi'_0)}$,
    en se souvenant que la fonction cosinus est une fonction sinus déphasée de $-\pi/2$ :
    $\cos(\omega t +\varphi'_0)=\sin\left(\omega t +\varphi'_0-\dfrac{\pi}{2}\right)=\sin(\omega t +\varphi_0)$$\quad \Longrightarrow\quad\Delta\varphi = \varphi'_0 - \varphi_0 = -\dfrac{\pi}{2}$

  • Lorsque l'effet observé ou recherché ne dépend pas de la phase du courant, ou de la différence de phase entre deux courants, alors la phase à l'origine $\varphi_0$ peut être négligée dans l'écriture mathématique :
    $\mathbf{I(t)=I_0 \sin(\omega t)\quad}$ ou $\quad\mathbf{I(t)=I_0 \cos(\omega t)}$

!! Pour aller plus loin : !! !! L'intérêt de la fonction harmonique (au-delà de son application à la stricte intensité d'un courant électrique, vient du théorème de Fourier qui stipule que :
!! * toute fonction arbitraire du temps peut se décomposer en une superposition (somme ou intégrale) de fonctions harmoniques du temps, de différentes amplitudes, pulsations et phases à l'origine, !! !! appliqué aux systèmes linéaires, c'est à dire dont : !! * la réponse à une fonction arbitraire temporelle $f(t)$ est la superposition (somme ou intégrale) des réponses du système à chacune des composantes harmoniques de $f(t)$. !! !! Dans ce cas, les calculs seront fortement simplifiés voire uniquement possibles en utilisant la notation complexe $\underline{f(t)}$ de la fonction harmonique $f(t)$. !! !! La notation en cosinus $f(t)=f_0\cdot \cos(\omega t + \varphi'_0)$ est alors à privilégier, parce que le lien avec la notation complexe est simple. Le signal décrit par la fonction harmonique réelle $f(t)$ s'exprime alors comme la partie réelle $f(t)=\mathcal{R}[\underline{f(t)}]$ de la fonction harmonique complexe $\underline{f(t)}$ qui s'écrit :
!! $\underline{f(t)}=f_0\cdot e^{\,i\,(\omega t + \varphi_0)}$$\;=f_0\cdot e^{\,i\,\varphi_0}\cdot e^{\,i\,\omega t}$$\;=\underline{f_0}\cdot e^{\,i\,\omega t}$,
!! où $\;\underline{f_0}=f_0\cdot e^{\,i\,\varphi_0}$ désigne l'amplitude complexe de $\underline{f(t)}$. !! !! Nous utiliserons pour cela l'implication :
!! $e^{\,i\,\varphi(t)}=\cos \varphi(t) + i \cdot \sin \varphi(t)$$\quad\Longrightarrow\quad f(t)=\mathcal{R}[\underline{f(t)}]$.

Quelle est la différence entre les conducteurs et les semi-conducteurs solides ?

à faire.

Après une description des phénomènes de transport, parler des différents types de porteurs de charges, électrons et trous (lacunes électroniques)

Que sont la vitesse de dérive et la mobilité ?

Vitesse de dérive d'un type de porteur de charge

• Dans un plasma peu dense, chaque particule libre de charge $q$ et de masse $m$ au repos est relativement libre de se déplacer. Sous l'effet de la force électrique $\overrightarrow{F_E}=q \cdot \overrightarrow{E}$, elle est accélérée $\overrightarrow{a}=\overrightarrow{F_E}/m$, et sa vitesse augmente constamment et peut atteindre des vitesses relativistes.

• Dans un matériau dense comme un conducteur solide, au cours de sa trajectoire chaque particule libre de charge $q$ subit pleins de "chocs" (expression classique) avec notamment les atomes du réseau matériel, qui relaxent sa quantité de mouvement et son énergie cinétique.
  
  $\Longrightarrow$ mouvement désordonné sans direction privilégiée, donc qui n'induit pas de courant électrique à travers une surface : c'est le mouvement d'agitation thermique.
  
  $\Longrightarrow$ à ce mouvement d'agitation thermique se superpose un lent mouvement de dérive en direction du champ électrique (matériaux isotropes) qui réaccélère la particule entre deux chocs : c'est un mouvement de dérive.

• Dans un volume mésoscopique de matériau conducteur et dans une description classique des forces moyennes qui agissent sur les particules libres chargées au sein de ce volume, les chocs agissent comme une force de frottement $\overrightarrow{F_{frot}}$ qui s'oppose à la force électrique $\overrightarrow{F_E}$.

• Lorsque ces deux forces sont égales en modules et de sens opposés $(\;\overrightarrow{F_{frot}}=-\overrightarrow{F_E}\;)$ , la force résultante s'annule, donc l'accélération moyenne s'annule et la population de particules chargées libres d'un même type se déplacent globalement d'un vecteur vitesse appelé vecteur vitesse de dérive $\overrightarrow{v_{d}}$.
  
  $\Longrightarrow$ de vitesse moyenne faible, mais de direction stable, le mouvement de dérive induit un courant électrique dans le matériau.

Mobilité d'un type de porteur de charge.

• Pour des valeurs de champ électrique pas "trop fort" (régime ohmique), la vitesse de dérive $\overrightarrow{v_d}$ est proportionnelle au champ électrique appliqué $\overrightarrow{E}$.

• La mobilité électrique est le rapport de proportionnalité entre les normes $||\overrightarrow{v_d}||$ et $||\overrightarrow{E}||$ des vecteurs vitesse de dérive et champ électrique :
  
  $\mathbf{||\,\overrightarrow{v_d}\,||=\mu \cdot ||\,\overrightarrow{E}}\,||$

Unité SI : ampère par mètre carré par volt seconde : $\mathbf{m^2\,V^{-1}\,s^{-1}}$

! Note : Dans l'électrotechnique, la taille des composants étant plutôt de l'ordre du centimètre que du mètre, l'usage est d'utiliser l'unité $cm^2\,V^{-1}\,s^{-1}$ pour la mobilité.

! Note 2 : Un matériau dont les porteurs de charges ont une grande mobilité pour ses électrons libres par exemple, plus la vitesse de dérive des électrons sera importante pour un même champ électrique appliqué, plus le courant électrique sera important pour une même densité volumique en électrons libres. Par ailleurs, plus le matériau répondra en fréquence.

!! Pour aller plus loin : !! parler du fait que dans un matériau semi-conducteur donné, la mobilité des trous (libres) et en général plus faible que la mobilité des électrons libres. Donner l'exemple de la vitesse d'une voiture unique sur une rocade vide, et de la vitesse d'une "place libre" dans un rocade complètement bloquée par des voitures immobiles à touche-touche...

Qu'est-ce que le vecteur densité volumique de courant ?

Avec un seul type de porteur de charge

Soit un matériau solide conducteur soumis à un champ électrique extérieur $\overrightarrow{E}$.

• En un temps $dt$, en moyenne un porteur de charge libre parcourt un vecteur distance $\overrightarrow{dl}$ telle que : $\overrightarrow{dl}= \overrightarrow{v_d} \cdot dt$

Soit une petite surface mésoscopique $\overrightarrow{dS}$ orientée en direction et sens du courant électrique.

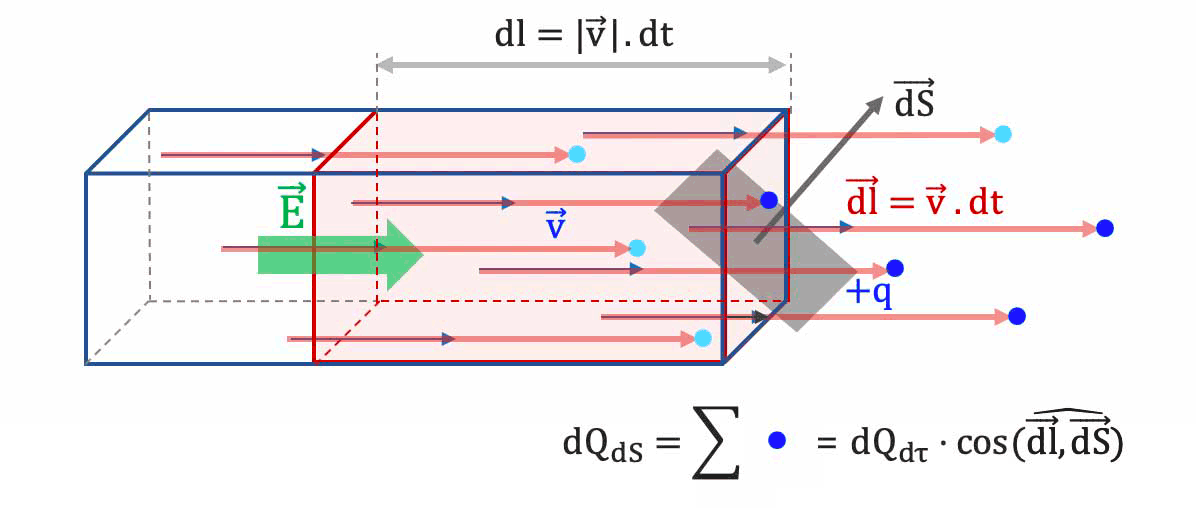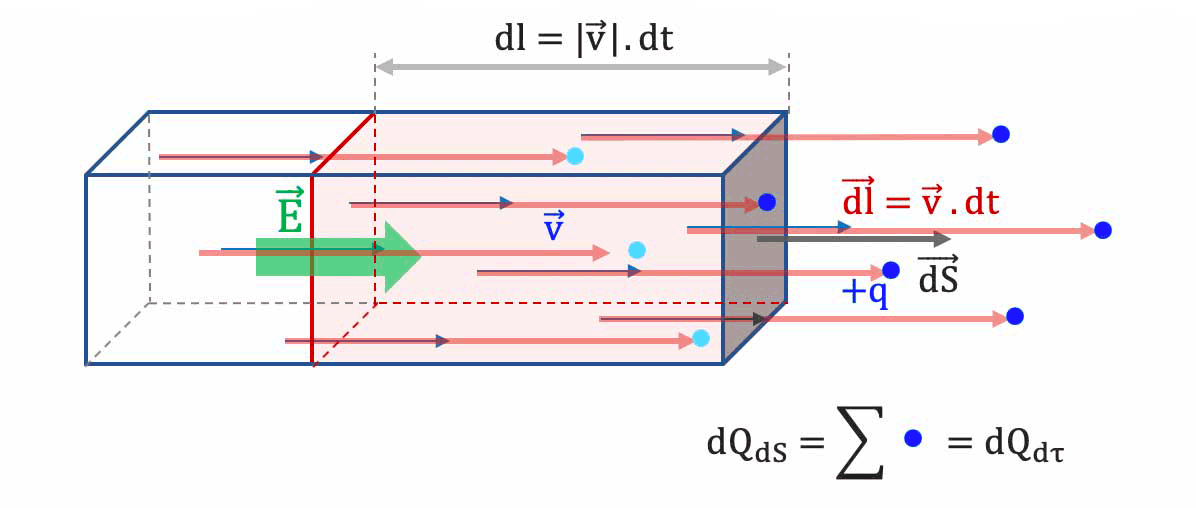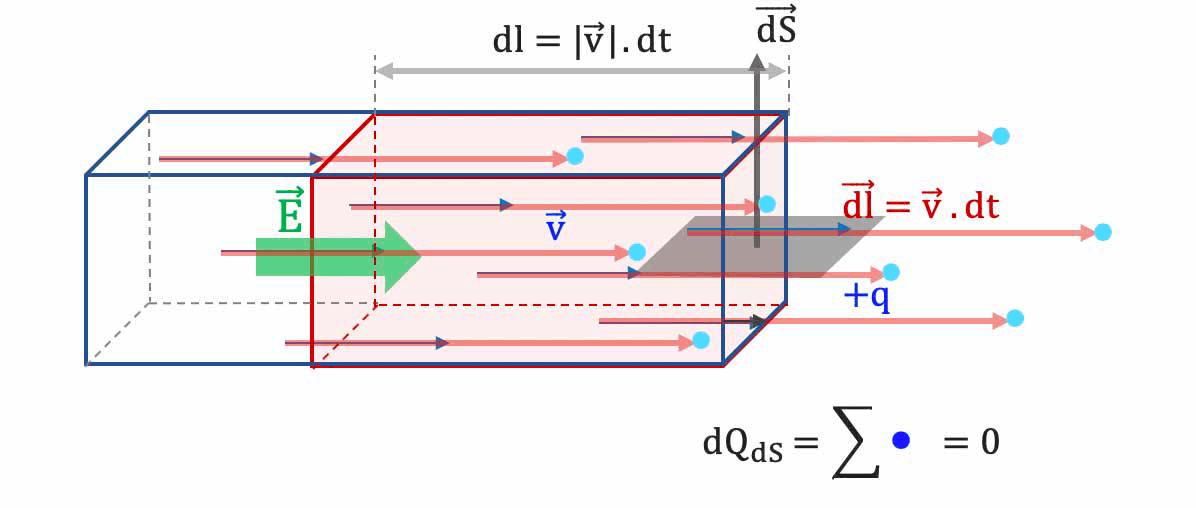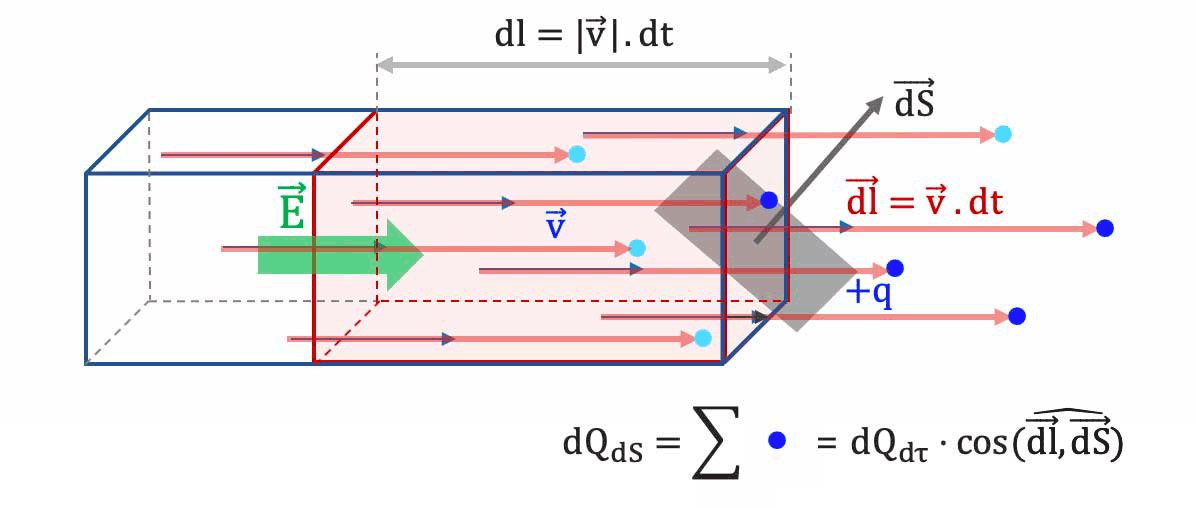
• Les porteurs qui traverseront en ce temps $dt$ la surface $\overrightarrow{dS}$ sont ceux situés dans le parallélépipède rectangle de section $dS$ et de longueur $d$, donc de volume mésoscopique $d\tau$ tel que :
  $d\tau = dl \cdot dS = ||\overrightarrow{v_d}|| \cdot dt\cdot dS$.

• La charge totale $dQ_{dS}$ qui traverse dans le temps $dt$ est donc la charge

• totale $dQ_{d\tau}$ des porteurs de charge libres contenus dans le volume $d\tau$.

• La charge totale $dQ_{dS}$ qui traverse dans le temps est donc la charge totale $dQ_{d\tau}$ des porteurs de charge libres contenus dans le volume . Cette charge totale $dQ_{dS}=dQ_{d\tau} \;(C)$ est donc le produit de la densité volumique de charges libres $\rho \;(C\,m^{-3})$ dans le matériau multipliée par le volume $d\tau \; (m^{-3})$.

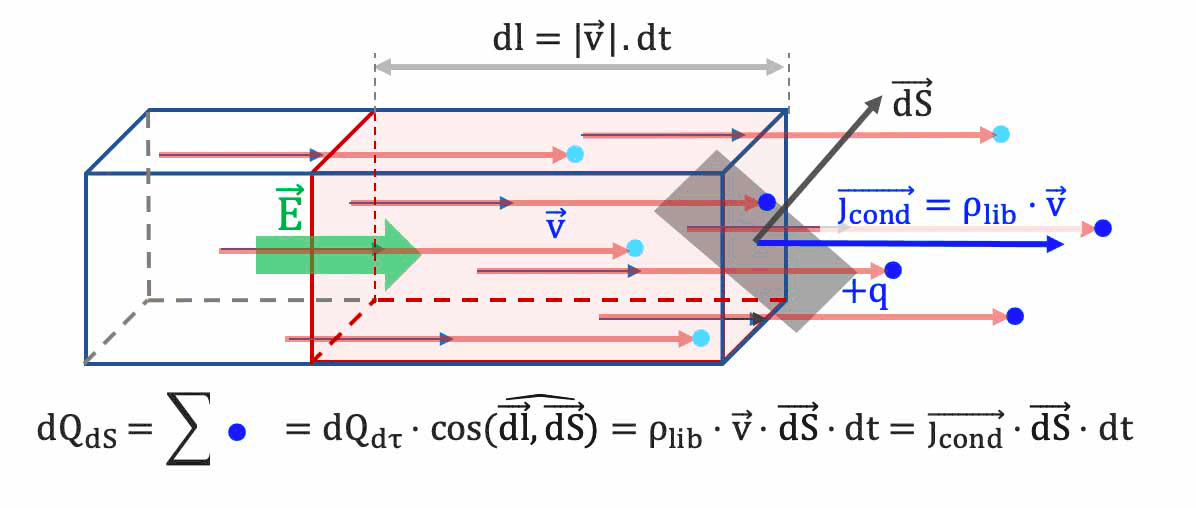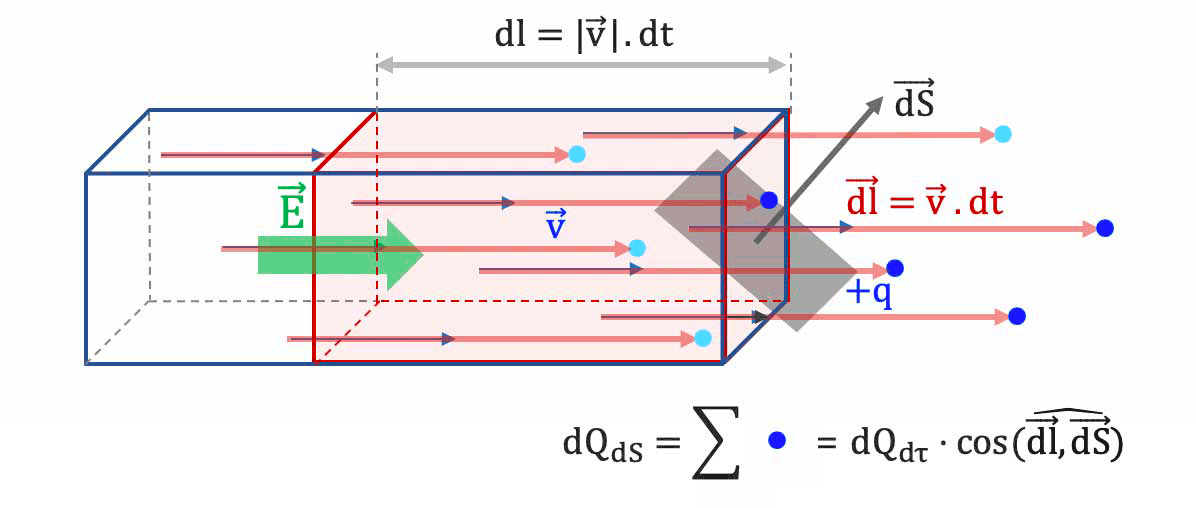
• Nous appelons vecteur densité volumique de courant (de conduction) $\overrightarrow{j_{cond}}$ le produit de la densité volumique de charges libres $\rho_{lib}$ par le vecteur vitesse de dérive $\overrightarrow{v_{d}}$ des porteurs libres de ces charges :
  
  $\mathbf{\overrightarrow{j_{cond}} = \rho_{lib} \cdot \overrightarrow{v_d}}$

• Équation aux dimensions et unité SI du vecteur densité volumique de courant :
  
  $[j_{cond}] = [rho_{lib}] \cdot [{v_d}]= [Q] \cdot L^{-3} \cdot L \cdot T^{-1}$ $\;= [Q] \cdot T^{-1} \cdot L^{-2}= I \cdot L^{-2}$
  
  Unité SI : ampère par mètre carré : $\mathbf{Am^{-2}}$

• L'intensité $dI$ qui traverse en un temps $dt$ cette surface $dS$ s'exprime donc :
  
  $dI = \dfrac{dQ_{dS}}{dt}= \dfrac{dQ_{d\tau}}{dt} = \rho_{lib} \cdot \overrightarrow{v_d} \cdot dt \cdot \overrightarrow{dS}$ $\quad\Longrightarrow$$\mathbf{\quad dI = \overrightarrow{j_{cond}} \cdot \overrightarrow{dS}}$

Cette formule s'applique même si la surface n'est orientée ni en sens ni en direction du vecteur de dérive.

Avec plusieurs types de porteurs de charge

• Lorsque plusieurs types de porteurs de charge libres existent au sein d'un conducteur donné, chaque type de porteur est plus ou moins mobile, est caractérisé par sa propre mobilité, et est donc animé de son propre vecteur vitesse de dérive dans un champ extérieur appliqué donné.

• Nous pouvons alors associé à chaque type de porteurs de charge libres son propre vecteur densité volumique de courant.

! Remarque : Remarque : des porteurs libres de charge négative donneront une densité volumique de charge négative et ont un vecteur vitesse de dérive de sens opposé au vecteur champ électrique. Les vecteur densité volumique de courant sera donc orienté dans le sens du champ électrique, donc dans le sens du courant électrique.
! Un raisonnement analogue pour des porteurs de charge positive soumis au même champ électrique donnerait le même résultat. ! ! $\Longrightarrow$ que les charges soient positives ou négatives, le vecteur densité volumique de courant est dirigé toujours dans le sens du champ électrique, donc dans le sens du courant électrique.

• Le vecteur densité volumique de courant total $\overrightarrow{j_{cond}}_{TOT}$ est la somme des vecteurs densité volumique de courant de chaque type de porteurs libres présents dans le conducteur.

• L'intensité du courant électrique s'exprime alors par :
  
  $\mathbf{dI = \overrightarrow{j_{cond}}_{TOT} \cdot \overrightarrow{dS}}$

Que représente le vecteur densité superficielle de courant ?

• Le monde réel possède trois dimensions spatiales, le vecteur densité volumique de courant est défini dans tout le volume d'un conducteur.

• Cependant, parfois l'une des dimensions spatiale peut être négligée, soit parce qu'elle apparait d'extension infime par rapport à notre domaine macroscopique d'étude, soit parce que nous ne connaissons pas le profil de variation du vecteur densité volumique de courant le long de cette dimension spatiale. Nous avons alors envie de faire disparaitre cette dimension spatiale de notre étude.

!!! Exemple :
!!! Exemple : un rouleau de feuille d'aluminium est déroulé, et sert à conduire le courant dans le sens de sa longueur. Une section de ce papier conducteur perpendiculaire au courant électrique qu'il transporte peut avoir une longueur de 20cm, mais qu'elle est son épaisseur e? Je ne connais pas cette épaisseur, elle est à la limite de ce que je peux discerner à mon échelle, et bien sûr je ne connais pas le distribution du courant le long de cette épaisseur. Je souhaite donc faire disparaître cette variable e de mon étude.

• Faire disparaître une dimension spatiale revient à passer d'une description 3D du monde réel à une modélisation simplifiée 2D de celui-ci.

• L'intensité réelle $dI$ à travers un vecteur surface élémentaire $\overrightarrow{dS}$ rectangulaire d'extension $dl$ et $de$ selon ses deux côtés, s'exprime en fonction du vecteur densité volumique de courant $\overrightarrow{j_{cond}}$ par :
  
  $dI = \overrightarrow{j_{cond}}_{TOT} \cdot \overrightarrow{dS} = \overrightarrow{j_{cond}}_{TOT} \cdot dS \cdot \overrightarrow{n}$ $\quad= \overrightarrow{j_{cond}}_{TOT} \cdot de \cdot dl \cdot\overrightarrow{n}$

• Pour faire disparaître la dimension d'extension $de$ , je l'unie au vecteur densité volumique de courant, définissant ainsi une nouvelle grandeur physique : le vecteur densité superficiel (ou surfacique) de courant , définit par :
  
  $dI = (\,\overrightarrow{j} \cdot de\;) \cdot dl \cdot\overrightarrow{n} = \overrightarrow{j_S}\cdot dl \cdot\overrightarrow{n} $

• L'intensité totale le long de la ligne de longueur $L$, dimension spatiale restante de la section $S$ à travers laquelle le courant électrique est mesuré, s'exprime donc :
  
  $\displaystyle\mathbf{I= \int_S dI = \int_L ( \overrightarrow{j_S}\cdot \overrightarrow{n}) \cdot dl}$

Que sont la conductivité et la résistivité ?

• Le vecteur densité volumique de courant

• Dans un conducteur solide, sous l'effet d'un champ électrique $\overrightarrow{E}$, les porteurs de charges caractérisés par une mobilité $\mu$ atteignent une vitesse de dérive $\overrightarrow{v_d}$ telle que :
  
  $||\,\overrightarrow{v_d}\,||=\mu\cdot||\,\overrightarrow{E}\,||$

Qu'est-ce que la loi d'Ohm?

La loi d'Ohm locale

• La loi d'Ohm locale dit que en tout point d'un conducteur ohmique, le vecteur densité volumique de courant $\overrightarrow{j}$ est proportionnel au champ électrique $\overrightarrow{E}$ :
  
  $\mathbf{\overrightarrow{j_{cond}}=\sigma \cdot \overrightarrow{E}}$

• La conductivité électrique $\rho$ caractérise les propriétés de conduction électrique d'un milieu matériel.
  Son unité SI est l' ohm par mètre $( \Omega m^{-1} )$.

• La résistivité électrique $\rho$ est l'inverse de la conductivité électrique.
  Son unité SI est le mètre par ohm $( \Omega^{-1} m )$ .

!!!! Attention : ne pas confondre résistivité électrique et densité volumique de charge, représentés par la même lettre. On utilisera préférentiellement la conductivité .

! Note : Dans l'électrotechnique, de par la taille des composants, l'usage est d'utiliser les unités :
! * $( \Omega \; cm^{-1} )$ pour la conductivité électrique. ! * $\Omega^{-1} \; cm$ pour la conductivité électrique.

La loi d'Ohm intégrale

à préciser la démarche et les calculs complets

• Pour une résistance de section constante $S$ et de longueur $L$ réalisée dans un matériau homogène de conductivité électrique $\sigma$ , la loi d'Ohm locale permet de retrouver la loi d'Ohm intégrale :
  $U=R\cdot I$

Quelle équation indique la conservation de la charge ?

Principe de conservation de la charge électrique

Le principe de conservation de la charge électrique stipule qu'il ne peut y avoir ni création ni annihilation spontanée de charge électrique. Ce principe de conservation de la charge n'a jamais été pris en défaut.

! Note : même dans le domaine des particules élémentaires où de la masse peut-être convertie en énergie (E=m.c2), toute particule élémentaire ne peut être créée ou annihilée que simultanément avec son antiparticule de charge opposée. Ainsi la charge du système reste identique au cours de ce processus.

• Si la charge $Q_{\tau}(t)$ dans un volume $\tau$ (indéformable et immobile) diminue (respectivement augmente), c'est qu'une charge positive a quitté le volume, donc a traversé la surface délimitant le volume dans le sens positif (de l'intérieur vers l'extérieur), ou qu'un charge négative est entrée dans le volume, donc a traversé la surface dans le sens négatif. Dans ces deux cas, cela correspond à un flux positif (respectivement négatif) du vecteur densité volumique de courant à travers S.

Equation intégrale de la conservation de la charge électrique

• Soit $Q_{\tau}(t)$ la charge totale contenue dans le volume à l'instant.
  
  $\displaystyle Q_{\tau}=\iiint_{\tau} \rho \cdot d\tau$
  
  Si sur un temps $dt$, la charge dans le volume $\tau$ varie d'une quantité $dQ_{\tau}$ , alors :
  
  $dQ_{\tau}=Q_{\tau}(t+dt)-Q_{\tau}(t)$ $\displaystyle \quad= \iiint_{\tau} \rho(\overrightarrow{r},t+dt) \cdot d\tau - \iiint_{\tau} \rho(\overrightarrow{r},t) \cdot d\tau$ $\displaystyle \quad = \iiint_{\tau} [\rho(\overrightarrow{r},t+dt)-\rho(\overrightarrow{r},t)] \cdot d\tau $ $\displaystyle \quad = \iiint_{\tau} \dfrac{\partial \rho(\overrightarrow{r},t)}{\partial t} \cdot dt \cdot d\tau$
  
  Et le taux de variation $dQ_{\tau} / dt$ de la charge $Q_{\tau}$ dans le volume s'écrit :
  
  $\displaystyle \dfrac{dQ_{\tau}}{dt}=\dfrac{d}{dt}\iiint_{\tau} \rho \cdot d\tau= \iiint_{\tau} \dfrac{\partial \rho}{\partial t} \cdot d\tau$

• La charge $dQ_{\tau}$ ayant quitté (étant entrée dans) ne pouvant ni s'annihiler ni se créer spontanément au sein d'un volume, elle est égale à la charge $dQ_S$ ayant traversé dans le sens positif (dans le sens négatif) la surface $S$ délimitant $\tau$. Cette variation de charge $dQ_S$ à travers $S$ en un temps $dt$ est égale au courant $dI$ à travers la surface $S$, soit au flux du vecteur densité volumique de courant à travers $S$ :
  
  $\displaystyle \dfrac{dQ_S}{dt}= dI_S= \oint_S \overrightarrow{j} \cdot \overrightarrow{dS}$
  
  Variations charges $|dQ_{\tau}|$ et $|dQ_S|$ étant égales en valeur absolue, mais étant comptées avec des signes opposés (parce que est par convention orienté de l'intérieur vers l'extérieur),
  
  $-\dfrac{dQ_{\tau}}{dt}=\dfrac{dQ_S}{dt}$
  
  alors l'équation intégrale de conservation de la charge électrique s'écrit :
  
  $\displaystyle\mathbf{\iiint_{\tau} \dfrac{\partial \rho}{\partial t} \cdot d\tau+\oint_S \overrightarrow{j} \cdot \overrightarrow{dS} =0\quad}$(Eq. cons. charge)

Equation locale de la conservation de la charge électrique

Il ya plusieurs façons (équivalentes) de déduire la loi locale (ou différentielle) de conservation de la charge électrique.

• Le raisonnement précédent ne fait aucune référence à une contrainte de taille. Il reste valable si le volume $\tau$ tend vers 0 autour de chaque point de l'espace ( ($\tau \rightarrow d\tau$, volume mésoscopique).
  
  
  
  Repartons de l'équation (Eq. cons. charge)
  
  $\displaystyle \iiint_{\tau} \dfrac{\partial \rho}{\partial t} \cdot d\tau+\oint_S \overrightarrow{j} \cdot \overrightarrow{dS} =0$
  
  Le volume n'étant pas nul :
  
  $\displaystyle \dfrac{\iiint_{\tau} \frac{\partial \rho}{\partial t} \cdot d\tau}{\iiint_{\tau}d\tau }+ \dfrac{\oint_S \overrightarrow{j} \cdot \overrightarrow{dS}} {\iiint_{\tau} d\tau}=0$
  
  Faisons tendre ce volume vers 0 :
  
  $\displaystyle \lim_{\tau \rightarrow 0} \left(\dfrac{\iiint_{\tau} \frac{\partial \rho}{\partial t} \cdot d\tau}{\iiint_{\tau}d\tau }\right)+\lim_{\tau \rightarrow 0} \left(\dfrac{\oint_S \overrightarrow{j} \cdot \overrightarrow{dS}} {\iiint_{\tau} d\tau}\right)=0$
  
  Dans le volume infinitésimal centré sur un point M, au premier ordre la densité volumique moyenne de charge dans est la densité volumique de charge au point M.
  
  $\displaystyle\lim_{\tau \rightarrow 0} \left(\dfrac{\frac{\partial \rho}{\partial t} \cdot \iiint_{\tau} d\tau}{\iiint_{\tau}d\tau }\right)+ \lim_{\tau \rightarrow 0} \left(\dfrac{\oint_S \overrightarrow{j} \cdot \overrightarrow{dS}} {\iiint_{\tau} d\tau}\right)=0$
  
  Et en se souvenant de la définition de la divergence d'un champ vectoriel appliquée au champ du vecteur densité volumique de courant :
  
  $\displaystyle div \; \overrightarrow{j} = \lim_{\tau \rightarrow 0} \left(\dfrac{ \oint_S \overrightarrow{j} \cdot \overrightarrow{dS}} {\iiint_{\tau} d\tau}\right)$
  
  donc nous en déduisons l'équation locale de conservation de la charge électrique :
  
  $\mathbf{div \; \overrightarrow{j} +\dfrac{\partial \rho}{\partial t} =0\quad}$(Eq. cons. charge)


• Autre méthode (mais équivalente au total) :
  
  Repartons de l'équation (Eq. cons. charge) en transformant l'intégrale double sur la surface fermée S en intégrale triple sur le volume délimité par S, grâce au théorème de Green-Ostrogradsky :
  
  $\displaystyle \iiint_{\tau} \dfrac{\partial \rho}{\partial t} \cdot d\tau+\iiint_{\tau} div \, \overrightarrow{j} \cdot d\tau=0$
  
  Soit,
  
  $\displaystyle \iiint_{\tau} \dfrac{\partial \rho}{\partial t} \cdot d\tau=- \iiint_{\tau} div \, \overrightarrow{j} \cdot d\tau$
  
  Cette équation étant vérifiée quelque soit le volume considéré, étant donc indépendante de ce volume, c'est que que l'égalité est vérifiée par les intégrandes eux-mêmes :
  
  $\dfrac{\partial \rho}{\partial t}=- div \; \overrightarrow{j} $
  
  que l'on peut écrire sous la forme
  
  $\mathbf{div \; \overrightarrow{j} +\dfrac{\partial \rho}{\partial t} =0\quad}$(Eq. cons. charge)

Quelle est la loi d'Ohm ?

Un circuit conducteur est-il chargé ?

Probablement circuit conducteur en régime stationnaire ou lentement variable

Ca, ca va passer dans l'électrostatique de la matière :

ici des conducteurs

je prépare l'électrostatique des diélectriques