courses/12.temporary_ins/70.wave-optics/20.diffraction/cheatsheet.fr.md

title	published	routable	visible	lessons
Le phénomène de diffraction	true	false	false	{slug <nil>} {order <nil>}

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

Le phénomène de diffraction

Le phénomène de diffraction est observé lorsqu'une onde (sonores, mécaniques, électromagnétiques) rencontre un obstacle à sa libre propagation (un corps, une ouverture ou un motif tridimentionnel dans un plan) de taille inférieure ou voisine de sa longueur d'onde $\lambda$. Ce phénomène se traduit par une dispersion de l'onde après interaction avec interaction avec l'obstacle.

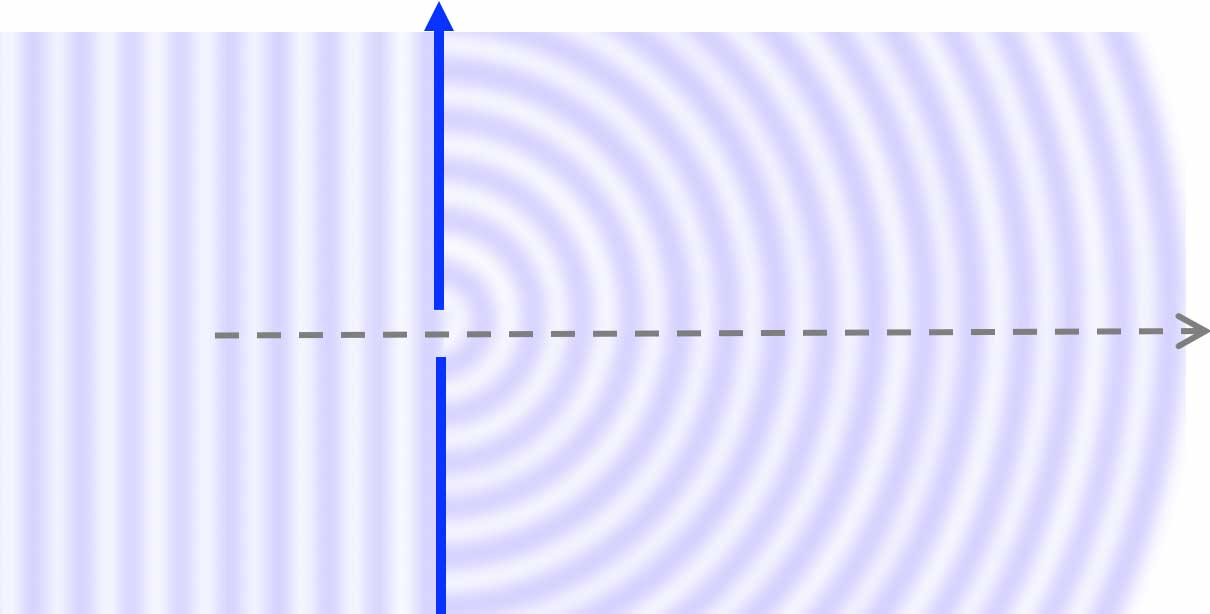
_Diffraction d'une onde plane à la surface de l'eau dans une cuve à onde, par un mur plan percé d'une fente [image libre de droit]. (L'obstacle mur n'apparaissant pas sur la photo originelle, il a été rajouté approximativement en gris sur cette image).

La lumière réalise le phénomène de diffraction. Lorsqu'un faisceau de lumière parallèle éclaire un écran opaque percé d'une toute petite ouverture, l'éclairement de la lumière transmise sur un second écran suffisamment loin du premier, je remarque que les dimensions de la tâche lumineuse observée ne correspondent pas à l'ombre portée de l'ouverture. Si un faisceau de lumière tombe sur une fente très fine d'épaisseur variable, l'ouverture angulaire du faisceau augmente à la traversée de la fente lorsque la largeur de la fente diminue.

Lorsqu'un faisceau de lumière parallèle éclaire un écran opaque percé d'une toute petite ouverture, et que j'étudie l'éclairement de la lumière transmise sur un second écran suffisamment loin du premier, je remarque que les dimensions de la tâche lumineuse observée ne correspondent pas à l'ombre portée de l'ouverture. Si un faisceau de lumière tombe sur une fente très fine d'épaisseur variable, l'ouverture angulaire du faisceau augmente à la traversée de la fente lorsque la largeur de la fente diminue.

Ce phénomène montre que la lumière est déviée lors de son passage au voisinage d'ouvertures ou d'obstacles de tailles caractéristiques proches de la longueur d'onde de la lumière, c'est le phénomène de diffraction de la lumière.

Ce phénomène est inexplicable dans le cadre de l'optique des rayons (optique géométrique) qui postule que la lumière se propage en ligne droite dans un milieu homogène et isotrope comme le vide ou l'air.

Le principe de Huygens-Fresnel

Le principe de Fresnel-Huygens stipule que :

---

• chaque point d'un front d'onde génère une onde sphérique, l'enveloppe de ces ondes sphériques secondaires constituant un nouveau front d'onde (contribution d'Huygens).

• Ces sources sphériques secondaires d'un même front d'onde sont mutuellement cohérentes. L'amplitude complexe de l'onde lumineuse résultante en tout point d'observation est la somme des amplitudes complexes de toutes ces sources secondaires (contribution de Fresnel).

---

Pour visualiser le principe de Huygens-Fresnel à l'aide d'un écran plan et opaque, éclairé par une onde plane monochromatique sous incidence normale :

• L'écran est percé d'une simple ouverture infinitésimale, l'onde transmise est alors une onde sphérique centrée sur l'ouverture de même longueur d'onde que celle de l'onde incidente. Il y a continuité de la phase de l'onde à la traversé de l'ouverture infinitésimale.

• L'écran est percé d'une ouverture étendue , chacun des points de l'ouverture plane est source d'une onde sphérique secondaire qui contribuera à l'onde transmise. Il y a continuité de la phase de l'onde à la traversée de chaque point de l'ouverture étendue.

• L'onde transmise est la résultante de l'infinité des ondes secondaires sphériques émises par chacun des points de l'ouverture plane étendue.

ATTENTION ; L'animation proposée ici illustre schématiquement le principe que tu reconstruis l'onde diffractée en faisant l'intégrale des contributions de l'infinité des sources sphériques secondaires. Mais la figure de diffraction finale obtenue est fausse, car seules quelques ondes sphériques ont été prises en compte dans l'image finale. Seul le calcul de l'amplitude puis de l'intensité résultantes en chaque point te permettra de connaitre l'onde transmise.[Contribution pour une animation schématique plus réaliste bienvenue]

! REMARQUE : ! ! Ainsi, l'étude du phénomène de diffraction se ramène à l'étude des interférences créés par une infinité d'ondes élémentaires, issues des sources secondaires uniformémenr réparties sur les pupilles. !

---

Description mathématiques du phénomène de diffraction à travers une ouverture rectangulaire.

Je me limite au cas d'une ouverture rectangulaire, éclairée sous incidence normale par une onde plane monochormatique de longueur d'onde $\lambda$.

! IMPORTANT : ! ! La longueur d'onde $\lambda$, caractérisant la période spatiale de l'onde, n'est pas une grandeur fondamentale de l'onde. Seules le grandeurs temporelles de l'onde comme la période temporelle $T$, sa fréquence (temporelle) $\nu$ ou sa pulsation $\omega$ sont des fréquences fondamentales car indépendantes du mileu de propagation de l'onde. À fréquence $\nu$ donnée, la longueur d'onde $\lambda$ dépend de la vitesse de propagation de l'onde $v$ selon la relation $\lambda=v/\nu$. Dans le cas de la lumière et plus généralement d'une onde électomagnétique, la longueur d'onde considérée sera toujours la longueur d'onde dans le vide. !

Pour étudier le phénomène de diffraction, je choisis le repère cartésien $(O, \overrightarrow{e_x},\overrightarrow{e_y},\overrightarrow{e_z})$ tel que :

• l'origine $O$ soit prise au centre de la pupille rectangulaire.
• l'onde plane incidente se propage en direction et sens du vecteur $\overrightarrow{e_z}$`.
• les côtés de la ouverture rectangulaire sont dirigés selon les vecteurs $\overrightarrow{e_x}$ et $\overrightarrow{e_y}$.

Les dimensions de l'ouverture' rectangulaire est $x_0$ selon $Ox$ et $y_0$ selon $Oy$.

Les sources secondaires émettant les ondes sphériques sont distribuées uniformément sur toute la surface de la pupille.

D'une manière générale, le calcul de l'intensité diffractée en un point $M(x,y,z)$ de l'espace repéré par le vecteur $\overrightarrow{OM} =\overrightarrow{r} = r\cdot\overrightarrow{u}$ situé dans le demi-espace $(z>0)$ se conduit en évaluant :

• la différence $\Delta s$ entre la distance $PM$ (distance de la source secondaire de surface élémentaire $dS$ située au point $P$ et le point $M$ et la distance $OM$ :
  $\Delta s=PM-OM$
• la différence de chemin optique $\delta$ corespondante :
  $\delta=n\cdot\Delta s$
  où $n$ est l'indice de réfraction caractérisant le milieu de propagation. Pour l'air et le vide, $n=1$`.
• la différence de phase au point $M$ entre l'onde émise par la source secondaire en $P$ et celle émise par source secondaire située à l'origine $O$, prise comme référence des phases :
  $\phi=\dfrac{2\pi\delta}{\lambda}$

La contribution $\underline{dA}$ (à un coefficient de proportionnalité près) d'une surface élémentaire $dS$ de la pupille $\mathscr{P}$ l'amplitude complexe totale au point M s'écrit :

• $\underline{dA}=e^{i\,\phi} dS$

L'amplitude complexe totale et l'intensité de l'onde diffractée se déduisent alors simplement

• $\displaystyle\underline{A}=\iint_{\mathscr{P}}\underline{dA}=\iint_{\mathscr{P}} e^{i\,\phi} dS$

• $I_{tot}=\underline{A}\,\underline{A}^{*}=|\,A^2\,| $

Diffraction en champ lointain

Diffraction en champ lointain =Diffraction à l'infini = Diffraction de Fraunhofer

Un cas particulièrement intéressant est le calcul de la diffraction en champ lointain.

En pratique, cela correspond à calculer ou à observer la figure dans un plan d'observation placé suffisamment loin de l'ouvertur $\mathscr{P}$ de façon à ce que les ondes sphériques secondaires puissent être approximées par des ondes planes au niveau du plan d'observation. Il faut pour cela que les rayons de courbure des ondes sphériques secondaires au niveau de l'écran d'observation soient très grands devant les dimensions de l'écran. La distribution d'intensité à l'infini est aussi réalisée (à un facteur d'échelle près) dans le plan focal image d'une lentille convergente.

La condition de validité est que la distance $d$ entre l'ouverture et le plan d'observation vérifie le critère $d\gg a^2/\lambda$, où a est la plus grande largeur de l'ouverture.

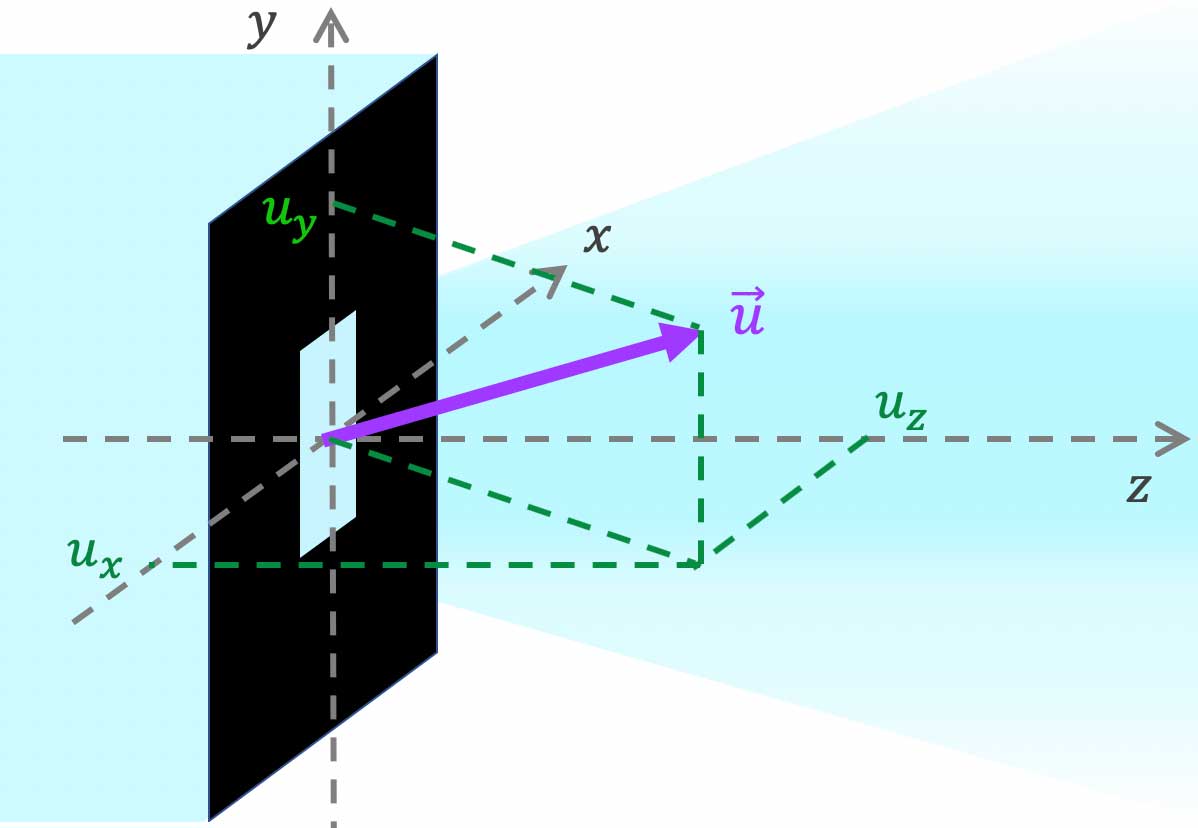
J'étudie la diffraction en champ lointain dans une direction donnée par le vecteur unitaire $\overrightarrow{u}$ :
$\overrightarrow{u}=u_x\cdot\overrightarrow{e_x}\;+\; u_y\cdot\overrightarrow{e_y}\;+\;u_z\cdot\overrightarrow{e_z}$

Pour une source secondaire située en un point P de coordonnées $(x_P, y_P, 0)$ de l'ouverture', que le point M d'observation se situe à très grande distance ou dans le plan focal image d'une lentille convergente, la distance algébrique $\overline{OH}=PM-OM$ s'exprime très simplement comme le produit scalaire $\overrightarrow{OP}\cdot\overrightarrow{u}$ :

$\overline{OH}=PM-OM=\overrightarrow{OP} \cdot\overrightarrow{u}$ $=u_x\cdot x_P\;+\;u_y\cdot y_P$

Si la lumière se propage dans l'air dont la valeur de l'indice de réfraction est $n=1$, la différence de chemin optique $\delta_P$ et la différence de phase $\phi_P$ caractérisant cette source secondaire s'écrivent :

$\delta=n\cdot(u_x\cdot x_P\,+\,u_y\cdot y_P)$

$\phi=\dfrac{2\,\pi\,\delta}{\lambda}= \dfrac{2\,\pi\,n\,(u_x\, x_P\;+\;u_y\, y_P)}{\lambda}$

L'amplitude complexe totale en M (à un facteur multiplicatif près) s'exprime alors

$\displaystyle\underline{A}=\iint_{\mathscr{P}} e^{\dfrac{i\,2\,\pi\,n\,(u_x\,x\,+\,u_y\,y)}{\lambda}}\;dx\,dy$

!! POUR ALLER PLUS LOIN : !! !! Ce résultat se généralise au cas où l'ouverture, appelée aussi pupille, introduit en chacun de ses points une différence de phase et une absoprtion variables, caractérisées par une fonction de transmittance complexe $t(x,y)$ appelée fonction pupillaire. !! !! L'amplitude complexe diffractée s'écrit alors :
!! $\displaystyle\underline{A}=\iint_{\mathscr{P}} t(x,y)\;e^{\dfrac{i\,2\,\pi\,n\,(u_x\,x_P\,+\,u_y\,y_P)}{\lambda}}\;dx\,dy$
!! Je reconnais ici la transformée de Fourier de la fonction pupillaire. !! !! Ce résultat est repris et développé dans ce qui constitue l'Optique de Fourier. L'optique de Fourier est un outil puissant pour la compréhension et la maîtrise entre autre du filtrage optique et de l'holographie. !! !! L'holographie permet l'enregistrement 2D et la reconstruction 3D d'ondes optiques. Elle permet de reconstituer une scène en vrai relief, contrairement aux diverses techniques de cinéma 3D actuelles. En vraie 3D, l'angle de vision sous lequel un spectateur observe l'image 3D reconstituée d'un objet change lorsque le spectateur se déplace. !!

Calcul 2D de l'intensité diffractée et de la figure de diffraction

Je calcule d'abord l'intensité diffracté dans le cas 2D, où l'onde incidente se propage en direction et sens du vecteur $\overrightarrow{e_z}$ et où la pupille centrée en $O$ et de dimension $x_0$ est parallèle au vecteur $\overrightarrow{e_x}$

L'amplitude complexe totale en M (à un facteur multiplicatif près) se limite alors à

$\displaystyle\underline{A}=\int_{\mathscr{P}} e^{\dfrac{i\,2\,\pi\,u_x\,x}{\lambda}}\;dx$ $\displaystyle=\int_{-x_0/2}^{+x_0/2} e^{\dfrac{i\,2\,\pi\,u_x\,x}{\lambda}}\;dx$

$\displaystyle \underline{A}=\dfrac{\lambda}{i\,2\,\pi\,u_x}\left(e^{\dfrac{i\,\pi\,u_x\,x_0}{\lambda}}-\;e^{\dfrac{-i\,\pi\,u_x\,x_0}{\lambda}}\right)$

$\displaystyle \underline{A}=-i\; \dfrac{\lambda}{i\,2\,\pi\,u_x}\left[ \left(cos\;\dfrac{\pi\,u_x\,x_0}{\lambda}+i\;sin\dfrac{\pi\,u_x\,x_0}{\lambda}\right)\right.$$\left.-\left( cos\;\dfrac{\pi\,u_x\,x_0}{\lambda}-i\;sin\;\dfrac{\pi\,u_x\,x_0}{\lambda}\right)\right]$

$\displaystyle \underline{A}=-i\; \dfrac{\lambda}{2\pi,u_x} \left( 2\,sin \;\dfrac{\pi\,u_x\,x_0}{\lambda}\right)$

Je réécris ce résultat sous la forme usuelle

$\displaystyle \underline{A}=-i\; x_0\cdot\dfrac{sin\,\dfrac{\pi\,u_x\,x_0}{\lambda}}{\dfrac{\pi\,u_x\,x_0}{\lambda}}$

qui fait apparaître la fonction sinus cardinal, notée $sinc\;u$ et définie par

$sinc\;u = \dfrac{sin\;u}{u}$.

L'intensité diffractée à l'infini en direction du vecteur unitaire $\overrightarrow{u}$, faisant un angle $\theta$ par rapport à l'axe $O$ est alors (à un facteur multiplicatif près) :

$I=x_0^2\cdot \dfrac{sin^2\,\left( \dfrac{\pi\,u_x\,x_0}{\lambda} \right)}{\left( \dfrac{\pi\,u_x\,x_0}{\lambda} \right)^2}$$\quad=x_0^2\cdot sinc^2\left( \dfrac{\pi\,u_x\,x_0}{\lambda} \right)$

---

Je souhaite exprimer l'intensité diffractée à l'infini en fonction de l'angle $\theta$ qui caractérise mieux visuellement la direction d'observation dans cette étude 2D.

Je remarque que

$ \overrightarrow{u}=u_x\cdot\overrightarrow{e_x}\;+\; u_z\cdot\overrightarrow{e_z}$ $=\;sin\,\theta\cdot\overrightarrow{e_x}\;+\;cos\,\theta\cdot\overrightarrow{e_z}$

ainsi l'intensité diffractée à l'infini se réécrit

$I(\theta)=x_0^2\cdot \dfrac{sin^2\,\left( \dfrac{\pi\,x_0\,sin\,\theta}{\lambda} \right)}{\left( \dfrac{\pi\,x_0\,sin\,\theta}{\lambda} \right)^2}$$\quad=x_0^2\cdot sinc^2\left( \dfrac{\pi\,x_0\,sin\,\theta}{\lambda} \right)$

---

J'observe maintenant la figure de diffraction à l'infini dans le plan focal image d'une lentille convergente.

J'utilise la lentille de distance focale image $f'$ dans les conditions de Gauss. Je choisis un repère de l'espace $(S, \overrightarrow{e_X}, \overrightarrow{e_Z})$ tel que

• $\overrightarrow{e_X}= \overrightarrow{e_x}\quad$ et $\quad\overrightarrow{e_Z}= \overrightarrow{e_z}$

• Les points $O$ et $S$ sont alignés sur l'axe $Oz$

La lentille est centré en $S$ et l'axe $Oz$ est son axe optique.

Les lois de l'optique des rayons dans l'approximation paraxiale (optique gaussienne) me disent que l'onde diffractée observée à l'infini dans la direction donnée par l'angle $\theta$ convergera en un point se coordonnée $X=f'\cdot \theta$.

! RAPPEL : ! ! L'expression géométrique exacte est $X=f'\cdot tan \,\theta$, mais dans les conditions de l'optique paraxiale (conditions de Gauss), l'angle $\theta$ reste petit, et les approximations utilisées en optique paraxiale
! $\quad\theta\;\simeq\;sin\,\theta\;\simeq\;tan\,\theta\quad$ lorsque $\theta$ est exprimé en radians,
! sont alors valables. !

L'intensité observée au point de coordonnée $X$ est l'intensité diffractée à l'infini (à un facteur près) par la pupille dans la direction $\theta$ , et son expression est

$I(X)=x_0^2\cdot \dfrac{sin^2\,\left( \dfrac{\pi\,x_0\,X}{\lambda\,f'} \right)}{\left( \dfrac{\pi\,x_0\,X}{\lambda\,f'} \right)^2}$$\quad=x_0^2\cdot sinc^2\left( \dfrac{\pi\,x_0\,X}{\lambda\,f'} \right)$

Propriétés et représentation des fonctions $sinc$ et $sinc^2$

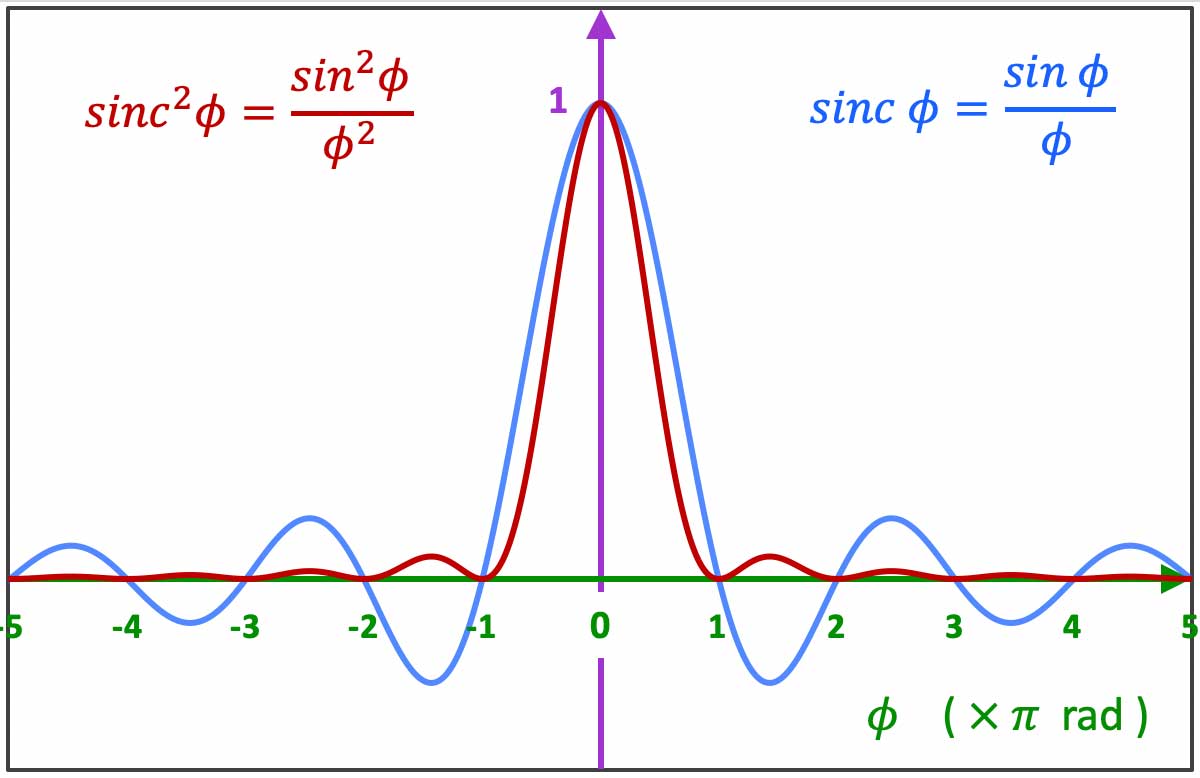
! IMPORTANT : ! ! La *fonction sinus cardinale $sinc\;\phi = \dfrac{sin\;\phi }{\phi }$ et son carré $sinc^2$ sont deux fonctions fondamentales qui interviennent dans de nombreux phénomènes ondulatoires en physique. !

• Ces fonctions $sinc \;\phi$ et $sinc^2\;\phi $ présentent chacune un maximum principal unique lorsque lorsque leurs dénominateurs s'annulent, à l'origine des phase $\phi=0$. La valeur de ce maximum unique est l'unité :
  $sinc\;0\;=\;1\quad$ et $\quad sinc^2 \;0 \;= \;1$

• Ces fonctions $sinc \;\phi$ et $sinc^2\;\phi $ s'annulent lorsque $\phi=0 \Longleftrightarrow \phi=k\;\pi$.

• La valeur des pics secondaires de la fonction $sinc^2$ décroissent très rapidement avec la valeur entière de k.

Calcul 3D de l'intensité diffractée et de la figure de diffraction

L'intensité diffracté dans le cas 3D s'obtient très facilement si le calcul 2D est fait. L''onde incidente se propage en direction et sens du vecteur $\overrightarrow{e_z}$. La pupille est centrée en $O$ et de dimensions $x_0$ selon le vecteur $\overrightarrow{e_x}$ et $y_0$ selon le vecteur $\overrightarrow{e_y}$

L'amplitude complexe totale en M (à un facteur multiplicatif près) se limite alors à

$\displaystyle\underline{A}=\iint_{\mathscr{P}} e^{\dfrac{i\,2\,\pi\,(u_x\,x+u_y\,y)}{\lambda}}\;dx$ $\displaystyle $

$\displaystyle\underline{A}=\int_{-x_0/2}^{+x_0/2} e^{\dfrac{i\,2\,\pi\,u_x\,x}{\lambda}}\;dx\;\int_{-y_0/2}^{+y_0/2}e^{\dfrac{i\,2\,\pi\,u_y\,y}{\lambda}}\;dy$

L'intensité diffractée apparait comme le produit de deux intégrales identiques à celle déjà calculée, j'obtiens donc :

$\displaystyle \underline{A}=- \; x_0\; y_0\cdot\dfrac{sin\,\dfrac{\pi\,u_x\,x_0}{\lambda}}{\dfrac{\pi\,u_x\,x_0}{\lambda}}\cdot\dfrac{sin\,\dfrac{\pi\,u_y\,y_0}{\lambda}}{\dfrac{\pi\,u_y\,y_0}{\lambda}}$

---

J'observe maintenant la figure de diffraction à l'infini dans le plan focal image d'une lentille convergente de distance focale image $f'$ utilisée dans les conditions de Gauss. Je choisis un repère de l'espace $(S, \overrightarrow{e_X}, \overrightarrow{e_Y} \overrightarrow{e_Z})$ tel que

• $\overrightarrow{e_X}= \overrightarrow{e_x}\quad$ et $\quad\overrightarrow{e_Z}= \overrightarrow{e_z}$

• Les points $O$ et $S$ sont alignés sur l'axe $Oz$

La lentille est alors centrée en $S$ dans le plan $XOY$ et l'axe $Oz$ est son axe optique.

L'intensité observée au point de coordonnées $(X,Y)$ s'écrit :

$I(X)=x_0^2\;y_0^2\cdot sinc^2\left( \dfrac{\pi\,x_0\,X}{\lambda\,f'} \right)\cdot sinc^2\left( \dfrac{\pi\,y_0\,Y}{\lambda\,f'} \right)$

Propriétés et représentation de l'intensité diffractée

Si je dois décrire la figure de diffraction observée, j'obtiens

[Nous avons besoin d'une photo libre de droits, présentant les figures de diffraction d'une fente recangulaire, pour différents rapports longueur/largeur]

• Un maximum central unique, rectangulaire et allongé dans la direction où la fente a sa plus petite dimension. ce maximum est très intense car il est le produit des maxima principaux selon les directions $X$ et $Y$.

• Sur chacun des axes $SX$ et $SY$ j'observe une série de maxima secondaires d'intensité, équivalente à celle calculée dans le cas 2D. L'intensité de chaque maximum secondaire est le produit de l'intensité d'un maximum secondaire de l'axe considéré par l'intensité du maximum principal de l'axe perpendiculaire à celui-ci.

• Hors des axes $X$ et $Y$, il existe des maxima tertiaires, mais d'intensités si faibles qu'ils sont quasiment invisibles à l'oeil humain.
  
  Le motif en croix résultant vient du fait que l'intensité totale est le produit des fonctions $sinc^2$ dans les deux directions $X$ et $Y$. En dehors des axes $X$ et $Y$, les maxima tertiaire d'intensité résultent du produit de deux maxima secondaires selon chacun des axes $X$ et $Y$. Chaque maxima secondaire ayant une intensité déjà faible par rapport à maximum principal, le produit de deux maxima secondaires devient très faible, et les maxima tertiaires hors axes sont quasi-invisibles.

Description mathématiques du phénomène de diffraction à travers une ouverture circulaire

L'étude du phénomène de diffraction par une ouverture circulaire est très important pour deux raisons complémentaires :

• Les instruments optiques comme les objectifs des appareils photo, les microscopes, les télescopes,

• utilisent des éléments optiques simples circulaires (lentilles, miroirs), et plus généralement

• présentent la symétrie de révolution et voient leurs faisceaux de lumière incidente limités par des ouvertures circulaires.

• le phénomène de diffraction dégrade l'image obtenue par ces systèmes, par rapport à ce qui est attendu en ne considérant que la simple optique géométrique. Ainsi l'image d'une source située à l'infini n'est pas ponctuelle dans le plan focal image de l'instrument, mais une tache, appelée tache d'Airy, dont le diamètre dépend de l'instrument et de la longueur d'onde de la lumière observée.

Diffraction en champ lointain

Conduire les calculs mathématiques pour une ouverture circulaire sont semblables à ce qui a été fait dans le cas de l'ouverture rectangulaire, mais je rencontrerai non pas une fonction sinus cardinale facile à calculer, mais une fonction spéciale appelé fonction de Bessel de premier ordre dont les valeurs sont tabulées et qui donc est moins facile à manipuler.

Ainsi la description mathématique de la figure de diffraction en champ lointain due à une ouverture circulaire, que je peux observer dans le plan focal image d'une lentille convergente s'exprime (à un facteur multiplicatif près) :

$I(X,Y)=I_0\;\left( 2\cdot \dfrac{J_1 \left( \dfrac{\pi\,D}{\lambda}\;\dfrac{\sqrt{X^2+Y^2}}{f'}\right)}{\dfrac{\pi\,D}{\lambda}\;\dfrac{\sqrt{X^2+Y^2}}{f'}}\right)^2$

où D est le diamètre de l'ouverture circulaire

$J_1$ est la fonction de Bessel de première espèce définie comme

$\displaystyle J_1(u)=\dfrac{-i}{2\,\pi}\;\int_0^{2\pi} e^{i\;u\,cos\,\phi} \; e^{i\,\phi} \; d\phi$

Ainsi exprimée, l'intensité observée $I(X,Y)$ dans le plan focal image décrit une tache centrale très brillante entourée d'anneaux concentriques d'intensités bien plus faibles et décroissantes lorsque la distance au centre croît. La tache centrale et les anneaux sont séparés par une extinction lumineuse. Cette figure de diffraction en champ lointain de l'ouverture circulaire, tache d'Airy, joue un rôle fondamentale dans la limite de résolution des instruments optiques.

Propriétés et représentation de la tache d'Airy

Si je dois décrire la tache d'Airy, j'obtiens

• un maximum principal unique centré sur l'origine

• un premier anneau d'extinction (intensité nulle) de rayon $R_0$$=\sqrt{X_0^2+Y_0^2}$ d'expression
  
  $R_0=1,22\;\dfrac{\lambda\;f'}{D}$

• une succession d'anneaux d'extinction séparés par des anneaux moins sombres. Les rayons normalisés $R\,/\,(\lambda f'/D)$ et les intensités relatives correspondantes $I(R)\,/\,I_0$ des 6 premiers maxima et minima sont
  
  

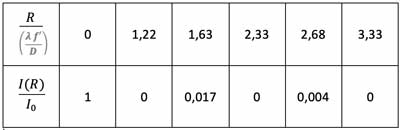
La dépendance du rayon $R_0=1,22\;\dfrac{\lambda\;f'}{D}$ en fonction de la longueur d'onde $\lambda$ et de l'inverse du diamètre $1\,/\;D$ implique deux faits importants :

• La dépendance en $1\,/\;D$ implique que plus grand est la diamètre d'ouverture d'un système optique, meilleure est la résolution de l'image qu'il rend.
  
  

!! POUR ALLER PLUS LOIN : !! !! Ainsi * en astronomie, augmenter le diamètre d'un télescope*, certes, *augmente la puissance lumineuse interceptée* par celui-ci et donc la *sensibilité* du télescope, son aptitude à observer des objects moins lumineux ou plus lointains dans l'univers. Mais et surtout cela *augmente la résolution des images* des objets observés, et permet de discerner de nouveaux détails sur les surfaces des corps astronomiques observés, ou encore de séparer des sources angulairement très proches (voir critère de Rayleight). !! !! En *microscopie optique*, lors de la conception d'un microscpe *le grossissement prévu* par l'optique paraxiale des rayons (suite à la sélection d'un objectif et d'un oculaire) *ne doit pas être dégradé* et donc limité par le *phénomène de diffraction*. !!

• La dépendance en $\lambda$ implique que lorsque l'ouverture reçoit une onde incidente polychromatique, chaque $\lambda$ produit sa propre tache d'Airy. Le maximum central est commun à chaque longueur d'onde (et apparait blanc si l'onde polychromatique est perçue blanche par l'oeil humain), mais un phénomène d'irisation est observé au fur dans les anneaux brillants secondaires.
  
  
  [Nous avons besoin d'une figure libre de droit montrant tache d'Airy d'un même objet observée a) en lumière quasi-monochromatique b) en lumière blanche]

Critère de Rayleight pour la tache d'Airy

Dans les instrument d'optique, le faisceau de rayons issu d'un point objet A est limité par un diaphragme qui peut être constitué par la monture des lentilles. L'image A' que donne l'instrument du point A n'est pas ponctuelle mais en réalité une petite tache de diffraction.

Les images de deux points voisins dans le plan objet constituent dans le plan image deux taches d'Airy. Je ne peux distinguer chacune de ces deux taches que si elles n'empiètent pas trop l'une sur l'autre.

Je me définis un critère intuitif et facilement quantifiable. Puisque je connais le rayon de la première extinction de la tache d'airy, le centre étant le maximum principal d'intensité, alors j'admets que mon oeil peut séparer deux taches d'Airy lorsque le centre de l'une se situe au-delà du premier minimum d'extinction de l'autre.

Le cas limite, qui me permet le choix entre discernabilité ou non discernabilité des deux taches, constitue le critère de Raylight.

Dans le cas d'une observation à travers un télescope de deux sources lumineuse lointaines caractérisées par la distance angulaire $\alpha$ qui les sépare, le critère de Rayleight précise que les deux sources pourront être discernées si $\alpha$ est supérieure ou égale à la distance angulaire minimal $\alpha_min$ telle que :

$\alpha_min=1,22 \dfrac{\lambda}{D}$

[Nous avons besoin d'une figure libre de droit qui montre la variation de distance entre deux tâches d'Airy lorsque $\alpha$ varie]