courses

🇨🇴 Una base de datos de cursos en diferentes lenguajes. 🇫🇷 Une base de données de cours dans différents langages. 🇳🇴 En database med kurs på forskjellige språk. 🇺🇸 A flat-file database of courses in multiple languages.

courses physics

32 KiB

Raw Blame History

title	published	routable	visible	lessons
Démonstration du théorème de Gauss	true	false	false	{slug gauss-ampere-theorems-demonstration} {order 1}

$\def\oiint{\displaystyle\mathop{{\iint}\mkern-18mu \scriptsize \bigcirc}}$ $\def\Ltau{\Large{\tau}\normalsize}$ $\def\Sopen{\mathscr{S}_{\smile}}$ $\def\Sclosed{\mathscr{S}_{\displaystyle\tiny\bigcirc}}$ $\def\Ssclosed{\mathscr{S}_{\scriptsize\bigcirc}}$ $\def\PSopen{\mathscr{S}_{\smile}}$ $\def\PSclosed{\mathscr{S}_{\displaystyle\tiny\bigcirc}}$

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à cette étape.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

! Thème :
! Electrostatique / Démonstration du théorème de Gauss, forme intégrale et forme locale
! Guide pour établir les 3 parties : main, overview, beyond
! ! (précède le thème : Electrostatique : Application du théorème de Gauss, forme intégrale et forme locale.)

ÉNONCÉS DU THÉORÈME DE GAUSS ( appliqué à l' ÉLECTROSTATIQUE )

Domaine de validité :

Électrostatique et Électromagnétisme.

Attention : Les expressions ci-dessous ne sont valables que dans le système international d'unité $SI$, anciennement $MKS$.

FORME INTÉGRALE

La flux du vecteur champ électrique $\overrightarrow{E}$ à travers toute surface fermée $S$ est égal à la charge électrique totale $Q_{int}$ (en valeur algébrique) située à l'intérieur de $S$ , multiplié par la constante électrique $\epsilon_0$ :

$\displaystyle\mathbf{\oiint_{S} \overrightarrow{E}\cdot\overrightarrow{dS}=\dfrac{Q_{int}}{\epsilon_0}}$

Différentes formulations de la charge intérieure :

charges discrètes $q_i$ : $Q_{int}=\sum_i q_i$
densité volumique de charge $\rho$ : $\displaystyle Q_{int}=\iiint_{\tau\leftrightarrow S} \rho\cdot d\tau $<br> avec $ \tau $ le volume délimité par $ S`$.

*FORME LOCALE*

En tout point de l'espace, la divergence du champ électrique $div\,\overrightarrow{E}$ est égal à la densité volumique de chrage en ce point $\rho$ divisée par la constante électrique $\epsilon_0$ :

$\mathbf{div\,\overrightarrow{E}=\dfrac{\rho}{\epsilon_0}}$

avec les unités $SI$ :

- champ électrique $E$ : $V\;m^{-1}$
- charge électrique $Q_{int},q_i$ : $ C$
- densité volumique de charge $\rho$ : $ C\;m^{-3}$
- $\epsilon_0=8,85418782\cdot 10^{-12}\;SI$

Quel est l'intérêt du théorème de Gauss intégral ?

Le théorème de Gauss est un théorème très général.
Il permet d'établir l'équation de conservation de toute grandeur physique.
Dans la limite ou une surface de Gauss tend vers 0, il permet de définir la notion de divergence qui quantifie une propriété locale de tout champ vectoriel :
$\Longrightarrow$ le théorème de Gauss aura une expression locale.
Cette notion de divergence est l'une des trois notions essentielles (avec le gradient et le rotationnel) pour décrire les lois de la physique au niveau universitaire.
Il permet de calculer les champs électrostatique $\overrightarrow{E}$ et gravitationnel $\mathcal{\overrightarrow{G}}$ lorsque les distributions de charge et de masse présentent des invariances et symétries, en remplaçant des calculs qui seraient extrêmement complexes.

Quels sont les concepts nécessaires pour comprendre le théorème de Gauss ?

Théorème = peut être démontré.
La démonstration nécessite de connaître les concepts de :
- angle solide.
- surface ouverte et surface fermée.
- flux à travers une surface.
- force centrale décroissante en $1/r^2$.
- théorème de superposition.
- divergence d'un champ vectoriel.

Qu'est-ce qu'un angle solide ?

Que représente-t-il ?

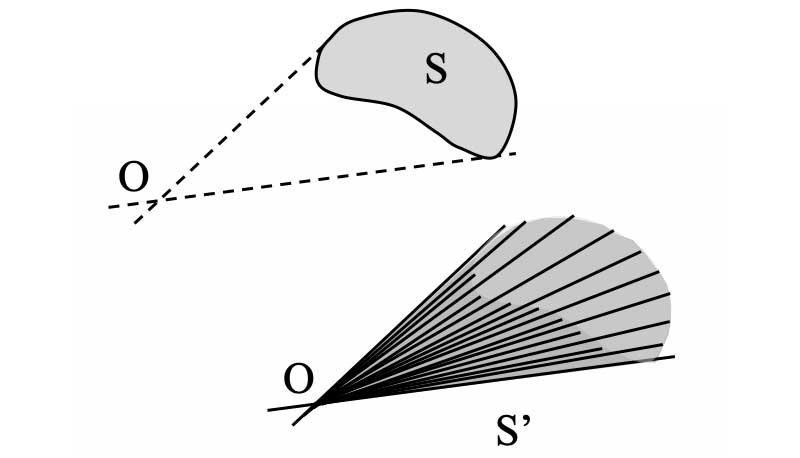
L’angle solide est une notion qui permet de définir et quantifier la portion d’espace
- sous laquelle un observateur voit depuis un point O une surface S dans cet espace.
- contenue à l’intérieur d’un faisceau de demi-droites d'origine $O$.

Comment le définir ?

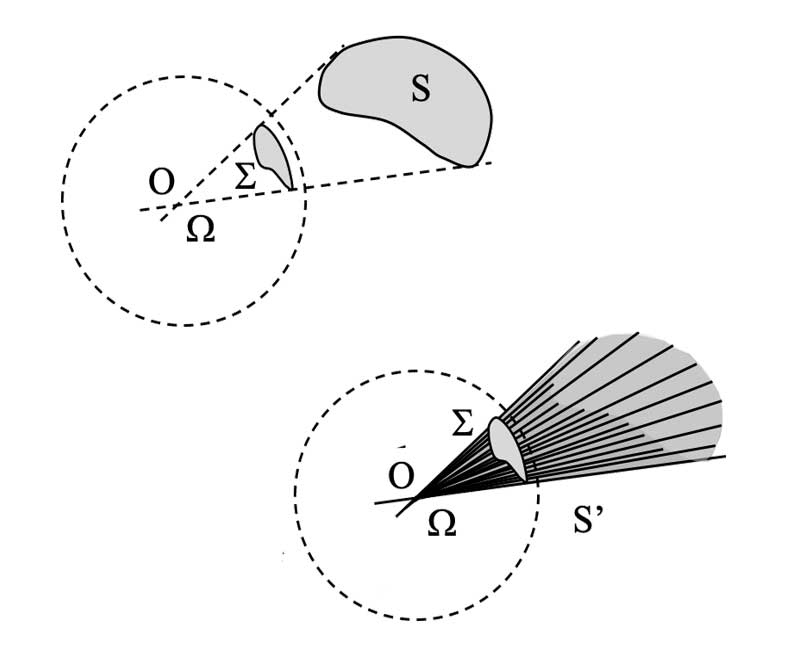
L’angle solide $\Omega$ est défini comme la surface $\Sigma$ obtenue par projection de la surface $S$ sur la sphère de centre $O$ et de rayon $R$, divisé par le rayon $R$ élevé au carré.

$\mathbf{\Omega=\dfrac{\Sigma}{R^2}}$
Ainsi exprimé, l’angle solide est une grandeur physique sans dimension. La valeur numérique de l’angle solide ainsi obtenue est l’angle solide exprimé en stéradian (sr).

Comment le calculer en pratique ?

Angle solide élémentaire $d\Omega$

Si le point $O$ et une surface élémentaire orientée $\overrightarrow{dS}$ de l’espace sont donnés, alors :

$\displaystyle\mathbf{d\Omega=\dfrac{|\,\overrightarrow{OM}\cdot\overrightarrow{dS}\,|}{OM^3}}\quad$, avec $OM=||\overrightarrow{OM}||$
En notation algébrique, l'angle solide élémentaire peut être positif ou négatif :

$\displaystyle\mathbf{d\Omega=\dfrac{\overrightarrow{OM}\cdot\overrightarrow{dS}}{OM^3}}\quad$, avec $OM=||\overrightarrow{OM}||$
Lorsque la surface est ouverte, deux sens sont possibles pour l’orientation des $\overrightarrow{dS}$, qui conditionnent le signe de l’angle solide.

Angle solide $\Omega$

Si le point $O$ et une surface orientée $S$ de l’espace sont donnés, alors :

$\displaystyle\mathbf{\Omega=\iint d\Omega=\iint_S \dfrac{|\,\overrightarrow{OM}\cdot\overrightarrow{dS}\,|}{OM^3}}\quad$, avec $OM=||\overrightarrow{OM}||$
En notation algébrique, l'angle solide peut être positif ou négatif :

$\displaystyle\mathbf{\Omega=\iint d\Omega=\iint_S \dfrac{\overrightarrow{OM}\cdot\overrightarrow{dS}}{OM^3}}\quad$, avec $OM=||\overrightarrow{OM}||$

Qu'est-ce qu'une surface ouverte ou fermée ?

surface fermée : frontière délimitant un volume intérieur et un espace extérieur.
$\Longrightarrow$ par convention :
- les éléments vectoriels de surface $\overrightarrow{dS}$ sont orientés de l'intérieur vers l'extérieur.
- l'intégration sur une surface fermée utilise le symbole $\oiint_S...\,dS$
surface ouverte : n'est pas la frontière d'un volume.
$\Longrightarrow$ :
- l'orientation des éléments vectoriels de surface $\overrightarrow{dS}$ doit être choisie parmi les deux sens possibles.
- l'intégration sur une surface fermée utilise le symbole $\displaystyle\iint_S...\,dS$.

Qu'est-ce que le flux d'un champ vectoriel à travers une surface ?

Flux élémentaire d'un champ vectoriel

Le flux élémentaire $d\Phi_X$ d'un champ vectoriel $\overrightarrow{X}$ est le flux de $\overrightarrow{X}$ à travers un élément vectoriel de surface $\overrightarrow{dS}$.
Par définition, $d\Phi_X$ est le produit scalaire $\overrightarrow{X}\cdot\overrightarrow{dS}$ : $\mathbf{d\Phi_X=\overrightarrow{X}\cdot\overrightarrow{dS}}$

Flux d'un champ vectoriel à travers une surface

$\Phi_X=\int d\Phi_X$
flux à travers une surface ouverte : $\displaystyle\mathbf{\Phi_X=\iint_S \overrightarrow{X}\cdot\overrightarrow{dS}}$.
flux à travers une surface fermée : $\displaystyle\mathbf{\Phi_X=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}}$.

Qu'est-ce qu'un champ de force centrale décroissante en $`1/r^2`$ ?

Force centrale : force d'interaction à distance, toujours dirigée en direction de sa source élémentaire.
(élémentaire = considérée comme °ponctuelle* à l'échellle d'observation).
Force décroissante en $1/r^2$ : force d'interaction à distance, dont l'intensité décroit comme le carré de la distance à sa source ponctuelle.
Expression générale d'un champ de force centrale décroissante en $1/r^2$ :

$\mathbf{\overrightarrow{X}=K\cdot x\cdot\dfrac{\overrightarrow{OM}}{OM^3}}\quad$, avec :

- $O$ : point où se situe la source élémentaire.
- $x$ : grandeur physique qui caractérise la sensibilité de la source élémentaire à l'interaction X.
- $M$ : point où est exprimé le champ de la force.
- $K$ : constante réelle qui dépend du système d'unités.
- $OM=||\overrightarrow{OM}||$.

et dans le repère sphérique $(O,\overrightarrow{e_r},\overrightarrow{e_{\theta}},\overrightarrow{e_{\varphi}})$ :

$\mathbf{\overrightarrow{X}=K\cdot\dfrac{x}{r^2}\cdot\overrightarrow{e_r}}\quad$
avec $r=OM\quad$ et $\quad\overrightarrow{e_r}=\dfrac{\overrightarrow{OM}}{OM}$.

!!! Exemples de champs de force centrale décroissantes en $1/r^2$ :
!!! - champ gravitationnel : $\mathcal{\overrightarrow{G}}=-\,G\cdot\dfrac{m}{r^2}\cdot\overrightarrow{e_r}$.
!!! - champ électrostatique : $\overrightarrow{E}=\dfrac{1}{4\pi\varepsilon_0}\;\dfrac{q}{r^2}\cdot\overrightarrow{e_r}$.
!!!

!!!

!!! Plus d'information sur ces deux expressions !!!

!!! Sont données en coordonnées sphériques :
!!! -expression du champ gravitationnel créé à une distance $r$ d'une source élémentaire de masse $m$ située en !!! $O$, G est la constante universelle de gravitation.
!!! -expression du champ électrique créé à une distance $r$ d'une source élémentaire de charge électrique $q$ immobile en $O$, $\varepsilon_0$ est la permittivité électrique du vide, encore appelée constante électrique. !!!

Quelle propriété particulière possède le flux d'un champ de force centrale décroissante en $`1/r^2`$ ?

Flux d'un champ de force centrale en $1/r^2$ à travers une surface fermée

Expression du flux élémentaire

$d\Phi_X=\overrightarrow{X}\cdot\overrightarrow{dS}$$\quad=\left(K\cdot x\cdot\dfrac{\overrightarrow{OM}}{OM^3}\right)\cdot\overrightarrow{dS}$$\quad=K\cdot x\cdot\left(\dfrac{\overrightarrow{OM}\cdot\overrightarrow{dS}}{OM^3}\right)$
$\mathbf{d\Phi_X=K\cdot x\cdot d\Omega}$

La surface fermée ne contient pas la source ponctuelle du champ

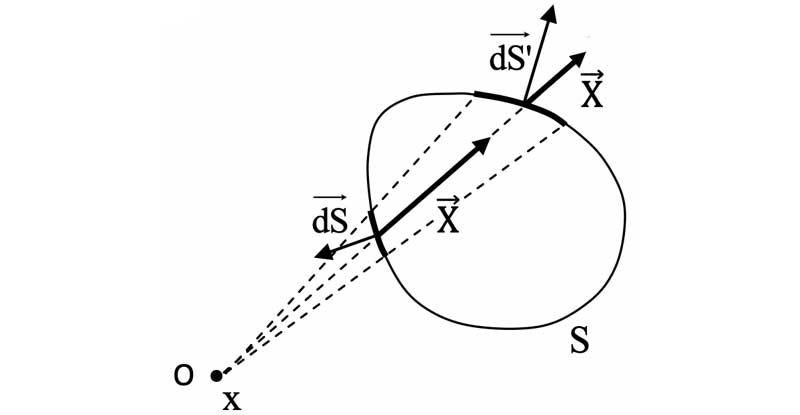
Partant de $O$, toute demi-droite $\Delta$ en direction de la surface $S$ traverse $S$ un nombre pair de fois .
Observé dans un même angle solide $d\Omega$ centré autour de $\Delta$, le flux élémentaire total $d\Phi_{\Delta}$ est égale à la somme d'un nombre pair $2n$ de flux élémentaires $d\Phi_i$ d'égales valeurs absolues.
Dans une moitié des cas : $0<\widehat{\overrightarrow{X}\overrightarrow{dS}}<\pi/2 \Longrightarrow d\Phi_i>0$,
dans l'autre moitié : $\pi/2<\widehat{\overrightarrow{X}\overrightarrow{dS}}<\pi \Longrightarrow d\Phi_i<0$

$\Longrightarrow$$\;d\Phi_{\Delta}=\sum d\Phi_i=0$.
$\Longrightarrow$ Le flux $\Phi_X$ à travers toute surface fermée qui ne contient pas la source de $X$ est nul :

$\mathbf{\Phi_X=\int_S d\Phi_{\Delta} =\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}=0}$

La surface fermée contient la source ponctuelle du champ

Partant de $O$, toute demi-droite $\Delta$ en direction de la surface $S$ traverse $S$ un nombre impair de fois .
Observé dans un même angle solide $d\Omega$ centré autour de $\Delta$, le flux élémentaire total $d\Phi_{\Delta}$ est égale à la somme d'un nombre impair $2n+1$ de flux élémentaires $d\Phi_i$ d'égales valeurs absolues.
$2n$ flux élémentaires s'annulent, et le flux élémentaire total $d\Phi_{\Delta}$ est égal au flux restant :

$\Longrightarrow$$\; d\Phi_{\Delta}=\sum d\Phi_i=K\cdot x\cdot d\Omega\quad$, avec $d\Phi_{\Delta}>0\;\Longleftrightarrow\;x>0$.
Le flux $\Phi_X$ à travers toute surface fermée qui contient la source de $X$ est égal à :
$\Phi_X=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}=\int_{\Omega_S} K\cdot x\cdot d\Omega$
Depuis le point $O$ situé à l'intérieur de la surface fermée $S$, l'angle solide $\Omega_S$ sous lequel est vue $S$ est de $4\pi$ stéradians : $\Omega_S=2\pi\;\text{sr}$
$\Longrightarrow$ Le flux $\Phi_X$ à travers toute surface fermée qui contient pas la source de $X$ est nul :

$\mathbf{\Phi_X=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}=4\pi\,K\,x}$

Qu'est-ce que le théorème de superposition ?

La présence ou non d'autre sources n'influence pas le champ $\overrightarrow{X}_{tot}$ créé chaque une source élémentaire. Donc le champ total $ X$ créé par une distribution de sources élémentaires est la somme des champs $X$ créé par chacune des sources élémentaires.
$\Longrightarrow$ :
- pour une distribution discrète de sources : $\mathbf{\overrightarrow{X}_{tot}=\sum_i \overrightarrow{X}_i}$.
- pour une distribution continue de sources : $\displaystyle\mathbf{\overrightarrow{X}_{tot}=\int d\overrightarrow{X}}$.

Que devient le flux à travers une surface fermée contenant plusieurs sources de champ ?

Soit $S$ une surface fermée dans l'espace démilitant un volume $\tau$.
Si $S$ contient en un point $P_1$ une unique source $x_1$ créant une champ vectoriel $\overrightarrow{X_1}$ central décroissant en $1/r^2$, le flux $\Phi_{X_1}$ de $\overrightarrow{X_1}$ à travers $S$ s'écrit :
$\mathbf{\Phi_{X_1}=\oiint_S \overrightarrow{X_1}\cdot\overrightarrow{dS}=4\pi\,K\, x_1}$
Si $S$ contient en un autre point $P_2$ une unique autre source $x_2$, de même le flux flux $\Phi_{X_2}$ s'écrit :
$\mathbf{\Phi_{X_2}=\oiint_S \overrightarrow{X_1}\cdot\overrightarrow{dS}=4\pi\,K\, x_2}$
Si les sources $x_1$ et $x_2$ existent simultanément, alors le théorème de superposition dit qu'en tout point de l'espace, le champ électrostatique total $\overrightarrow{X}$ est la somme des champs $\overrightarrow{X_1}$ et $\overrightarrow{X_2}$ :
$\overrightarrow{X}=\overrightarrow{X_1}+\overrightarrow{X_2}$
$\Longrightarrow$ le flux total de $\overrightarrow{X}$ à travers $S$ s'écrit :
$\Phi_{X}=\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}$ $\quad=\oiint_S (\overrightarrow{X_1}+\overrightarrow{X_2})\cdot\overrightarrow{dS}$ $\quad=\oiint_S \overrightarrow{X_1}\cdot\overrightarrow{dS}+\oiint_S \overrightarrow{X_2}\cdot\overrightarrow{dS}$
**$`\mathbf{\Phi_{X}=4\pi,K,(s_1+s_2)}$**
Ce résultat se généralise facilement à tout nombre entier de sources discrètes $x_i$ ou à une distribution continue de densité volumique $\rho_x(\overrightarrow{r})$
- pour n sources discrètes : $\displaystyle\mathbf{\quad\Phi_{X}=4\pi\,K\,\sum_{i=1}^n s_i}$
- pour une densité volumique $\mathbf{\rho_x(\overrightarrow{r})}$ : $\displaystyle\mathbf{\quad\Phi_{X}=4\pi\,K\,\iiint_{\Ltau} \rho_x(\overrightarrow{r})\cdot d\tau}$

Que dit le théorème de Gauss intégral en électrostatique ?

L'interaction électrostatique

La charge électrique, de symbole $q$, est la grandeur physique $x$ qui caractérise la sensibilté d'un corps à l'interaction électrostatique (et plus généralement l'interaction électromagnétique).
La charge $q$ peut être négative ou positive.
La force d'interaction électrostatique $\overrightarrow{F}_{1\rightarrow 2}$ qu'exerce une particule de charge $q_1$ immobile en $M_1$ sur une autre particule de charge $q_2$ située en $M_2$ s'écrit :
$\mathbf{\overrightarrow{F}_{1\rightarrow 2}=\dfrac{1}{4\pi\,\epsilon_0}\cdot q_1\,q_2\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}}$
C'est une force centrale décroissant en $1/r^2$$\quad\Longrightarrow$ le théorème de Gauss s'applique.
Cette force se réécrit :
$\overrightarrow{F}_{1\rightarrow 2}=q_2\cdot \overrightarrow{E_{1,M_2}}$
où $\overrightarrow{E_{1,M_2}}$ est le champ électrostatique créé par la particule immobile en $M_1$ au point $M_2$ :
$\overrightarrow{E}_{1\rightarrow 2}=\dfrac{1}{4\pi\,\epsilon_0}\cdot q_1\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}$
C'est une force centrale décroissant en $1/r^2$.
Le champ électrostatique créé en tout point $M$ de l'espace par une particule de charge $'q $ immobile en un point $ O $ s'écrit :<br> **$ \mathbf{\overrightarrow{E}=\dfrac{1}{4\pi,\epsilon_0}\cdot q\cdot \dfrac{\overrightarrow{OM}}{OM^3}}`$**

Quel est le lien entre électrostatique et électromagnétisme ?

L'électrostatique décrit le champ électrique créé par des particules chargées immobile.
L'électromagnétisme généralise aux champs électrique et magnétiques créés par des particules chargées immobile ou en mouvement.

Le théorème de Gauss intégral en électrostatique

Soit une distribution de charges maintenues immobiles dans l'espace.
Théorème de Gauss :
Le flux $\Phi_E$ du vecteur champ électrique à travers toute surface fermée $S$ de l'espace est égal à la charge totale $Q_{int}$ contenue à l'intérieur de $S$ divisée par la constante électrique $\epsilon_0$.

$\mathbf{\Phi_E=\oiint_S \overrightarrow{E}\cdot\overrightarrow{dS}=\dfrac{Q_{int}}{\epsilon_0}}$

Quelles sont les différentes expression de $`Q_{int}`$ rencontrées?

Pour n charges discrètes $q_i$ dans le volume $\tau$ :
$\displaystyle\mathbf{Q_{int}=\sum_{i=1}^n q_i}$
Pour une densité volumique de charge $\mathbf{\rho(\overrightarrow{r})}$ (cas de la réalité 3D à l'échelle d'observation) :
$\displaystyle\mathbf{Q_{int}=\iiint_{\Ltau} \rho(\overrightarrow{r}) \cdot d\tau }$
Lorsque les charges sont réparties sur une surface $S$ (2D $\Longleftrightarrow$ une épaisseur 1D est négligée) avec une densité surfacique de charge $\mathbf{\sigma}$ :
$\displaystyle\mathbf{Q_{int}=\iint_{S\cap\Ltau} \sigma(\overrightarrow{r}) \cdot dS }$
Lorsque les charges sont réparties sur un fil $\Gamma$ (1D $\Longleftrightarrow$ une section 2D est négligée) avec une densité linéïque de charge $\mathbf{\lambda}$ :
$\displaystyle\mathbf{Q_{int}=\int_{\Gamma\cap\Ltau} \lambda(\overrightarrow{r}) \cdot dl }$

Que dit le théorème de Gauss intégral en gravitation ?

L'interaction gravitationnelle

La masse, de symbole $m$, est la grandeur physique $x$ qui caractérise la sensibilté d'un corps à l'interaction gravitationnelle.
La masse $m$ de la matière est toujours positive.
La force d'interaction gravitationnelle de Newton $\overrightarrow{F}_{1\rightarrow 2}$ qu'exerce un corps de masse $m_1$ en $M_1$ sur un autre corps de masse $m_2$ située en $M_2$ s'écrit :
$\mathbf{\overrightarrow{F}_{1\rightarrow 2}=-\;G\cdot m_1\,m_2\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}}$
où $G$ est la constante universelle de la gravitation.
C'est une force centrale décroissant en $1/r^2$$\quad\Longrightarrow$ le théorème de Gauss s'applique.
Cette force se réécrit :
$\overrightarrow{F}_{1\rightarrow 2}=m_2\cdot \overrightarrow{\Gamma_{1,M_2}}$
où $\overrightarrow{\Gamma_{1,M_2}}$ est le champ gravitationnel créé par le corps en $M_1$ au point $M_2$ :
$\overrightarrow{\Gamma}_{1\rightarrow 2}=\;G\cdot m_1\cdot \dfrac{\overrightarrow{M_1M_2}}{M_1M_2^3}$
C'est une force centrale décroissant en $1/r^2$.
Dans le cadre de la physique classique, le champ gravitationnel $\mathcal{\overrightarrow{G}}$ créé en tout point $M$ de l'espace par un corps de masse $'m $ situé un point $ O $ s'écrit :<br> **$ \mathbf{\mathcal{\overrightarrow{G}}=-;G\cdot m\cdot \dfrac{\overrightarrow{OM}}{OM^3}}`$**

Théorème de Gauss intégral en gravitation

Soit une distribution de masses dans l'espace.
Théorème de Gauss :
Le flux $\Phi_{\mathcal{G}}$ du vecteur champ de gravitation $\mathcal{\overrightarrow{G}}$ à travers toute surface fermée $S$ de l'espace est égal à la masse totale $m_{int}$ contenue à l'intérieur de $S$ multiplié par $4\pi\,G$, où $G$ est la constante la constante universelle de la gravitation.

$\mathbf{\Phi_{\mathcal{G}}=\oiint_S \mathcal{\overrightarrow{G}}\cdot\overrightarrow{dS}=-\,4\pi\,G\,m_{int}}$

Pourquoi le théorème de Gauss intégral est-il insuffisant ?

Champ électrique créé par 3 charges ponctuelles immobiles situées dans plan de représentation du champ électrostatique.

Dans les cas simples, l'oeil humain repère immédiatement les points ou les lignes de champ électrique convergent ou divergent, qui localisent les causes du champ électrostatique dans le plan d'observation.
Le théorème de Gauss intégral précise, lors d'un flux non nul du champ électrostatique à travers une surface fermée, la somme totale des charges contenues à l'origine de ce flux, mais ne permet pas la localisation précise des charges du champ électrostatique.
Il doit exister une propriété locale (à l'échelle mésoscopique, donc apparaissant ponctuelle à la résolution de l'observation) qui en tout point de l'espace relie le champ électrostatique à sa cause élémentaire locale.

Une idée pour relier une propriété locale du champ électrostatique à sa cause ?

Dans la démonstration du théorème de gauss (partie principale), aucune échelle de taille n'est précisée pour le choix de la surface fermée de Gauss, et donc du volume intérieur qu'elle définit.
$\Longrightarrow$ idée 1 : faire tendre la surface fermée vers une surface fermée mésoscopique qui entoure chaque point de résolution de l'espace, le flux ainsi calculé sera une propriété locale du champ.
$\Longrightarrow$ idée 2 : la charge déduite du théorème de Gauss est la charge située à l'intérieur du volume mésoscopique délimité par cette surface de Gauss, c'est ainsi une charge locale.
Cette idée est à la base de la notion de divergence d'un champ vectoriel.

Comment est définie la divergence d'un champ vectoriel X ?

Soit $dS$ un élément de surface fermée qui délimite un élement de volume $d\tau$ contenu dans un voisinage de tout point de l'espace.

La divergence de $\overrightarrow{X}$, définie en tout point de l'espace, est le flux $d\Phi_X$ de $\overrightarrow{X}$ à travers $dS$, divisé par le volume $d\tau$ :

$\mathbf{div\,\overrightarrow{X}=\displaystyle \lim_{\tau\leftrightarrow 0 \\ \tau \leftrightarrow S} \dfrac{\displaystyle\oiint_S \overrightarrow{X}\cdot\overrightarrow{dS}}{\displaystyle\iiint_{\tau} d\tau}=\dfrac{d\Phi_X}{d\tau}}$
$\Longrightarrow$$\mathbf{\quad d\Phi_X=div\,\overrightarrow{X}\cdot d\tau}$.

Que représente-t-elle ?

La champ de divergence de X est un champ scalaire : $div\;\overrightarrow{X}\in\mathbb{R}$

Le valeur absolue de la divergence $\mathbf{|\,div\;\overrightarrow{X}\,|}$ indique l'intensité du champ $\overrightarrow{X}$ ce point.
( $div\;\overrightarrow{X}=0$ indique un champ qui ne converge ni ne diverge en ce point)
Le signe de $\mathbf{div\;\overrightarrow{X}}$ indique si la vergence du champ $\mathbf{\overrightarrow{X}}$ en ce point.
- $\mathbf{div\;\overrightarrow{X}<0}$$\quad\Longleftrightarrow\quad$ le champ $\mathbf{\overrightarrow{X}}$ diverge.
- $\mathbf{div\;\overrightarrow{X}>0}$$\quad\Longleftrightarrow\quad$ le champ $\mathbf{\overrightarrow{X}}$ converge.

Comment se détermine son expression en coordonnées cartésiennes ?

Soit un élément de volume $d\tau=dx\,dy\,dz$ centré en tout point $M$ de l'espace.

Soit $\overrightarrow{X_M}$ le champ vectoriel au point $M$ dû à l'ensemble de ses sources dans l'espace.
Le flux $\Phi_X$ de $\overrightarrow{X}$ à travers la surface fermée $dS$ délimitant $d\tau$ est la somme des flux de $\overrightarrow{X}$ à travers chacune des six faces élémentaires constituant $dS$.

Les déplacements et surfaces en jeu étant infinitésimals, au premier ordre et pour chacune des faces :
le champ électrique moyen = champ au centre de la face.
$\mathbf{\quad\quad=\overrightarrow{X_M}\pm\left.\dfrac{\partial \overrightarrow{X}}{\partial x_i}\right|_M\cdot\dfrac{dx_i}{2}}$,
champ $\overrightarrow{X}$ en $M$ plus son taux de variation $\dfrac{\partial \overrightarrow{X}}{\partial x_i}$ fois le déplacement élémentaire $\pm\dfrac{dx_i}{2}$, positif ou négatif selon le sens du déplacement en direction de l'axe $Ox_i$.

La somme des flux sur deux faces opposées selon $Ox_i$ donne $\left.\dfrac{\partial E_{xi}}{\partial x_i}\right|_M\cdot dx\,dy\,dz$.
Le flux total $\Phi_X$ à travers les six faces de l'élément de volume donne $\left(\left.\dfrac{\partial X_x}{\partial x}\right|_M+\left.\dfrac{\partial X_y}{\partial y}\right|_M+\left.\dfrac{\partial X_z}{\partial z}\right|_M\right)\cdot dx\,dy\,dz$.
Le produit $dx\,dy\,dz$ étant le volume élémentaire $d\tau$, selon sa définition l'expression de la divergence de $\overrightarrow{X}$ en coordonnées cartésiennes s'écrit en tout point de l'espace :

$\mathbf{ div\,\overrightarrow{X}}$$\mathbf{\;=\dfrac{d\Phi_X}{d\tau}}$$\;\mathbf{=\dfrac{\partial X_x}{\partial x}+\dfrac{\partial X_y}{\partial y}+\dfrac{\partial X_z}{\partial z} }$

Qu'est-ce que le théorème de Green-Ostrogradsky, et comment le visualiser ?

Soit une surface fermée $S$ dans l'espace en présence d'un champ vectoriel $\overrightarrow{X}$.
Soit $\Phi_X$ le flux de $\overrightarrow{X}$ à travers la surface fermée $S$.

Le volume $\tau$ que délimite la surface $S$ se décompose mentalement en éléments de volume $d\tau$.
Le champ vectoriel $\overrightarrow{X}$ produit un flux élémentaire $d\Phi_X$ à travers chaque $d\tau$ délimités par des élements de surface fermée $dS$.

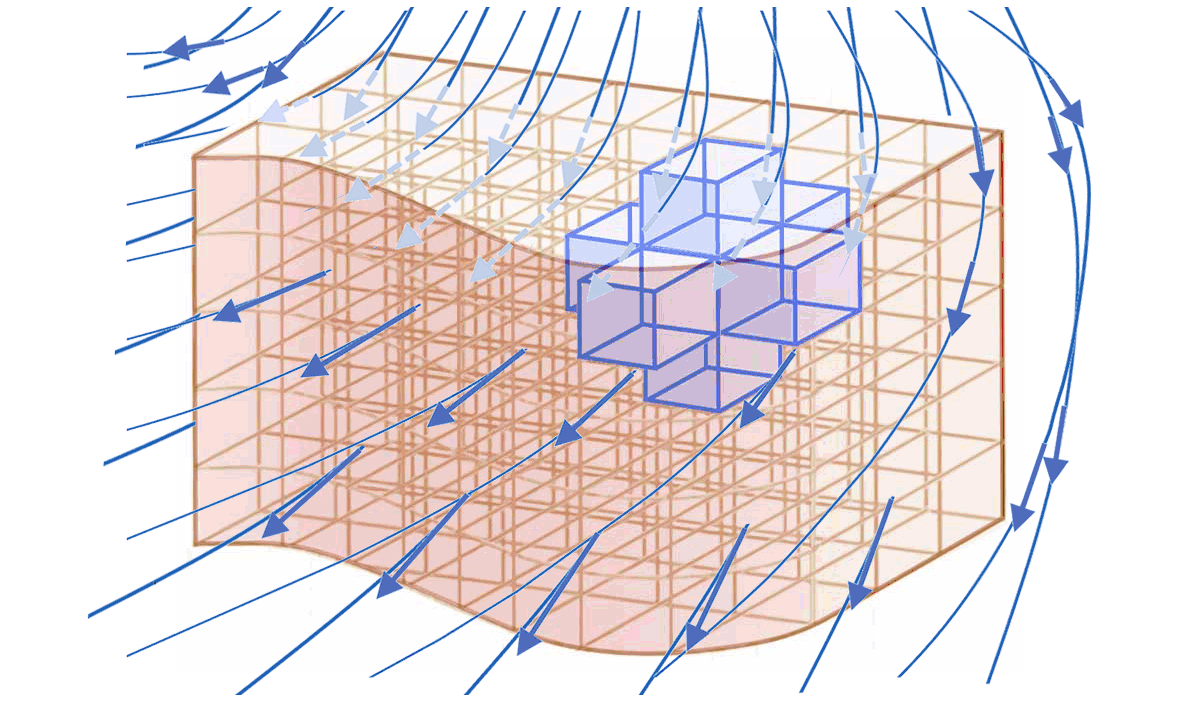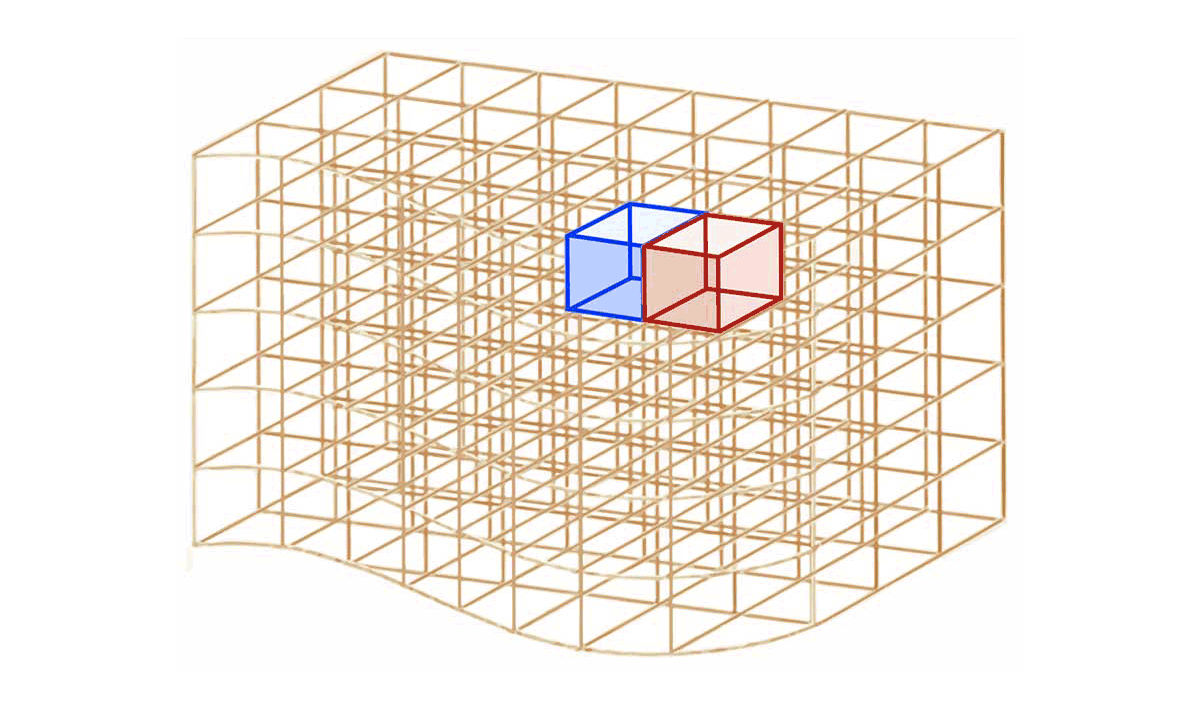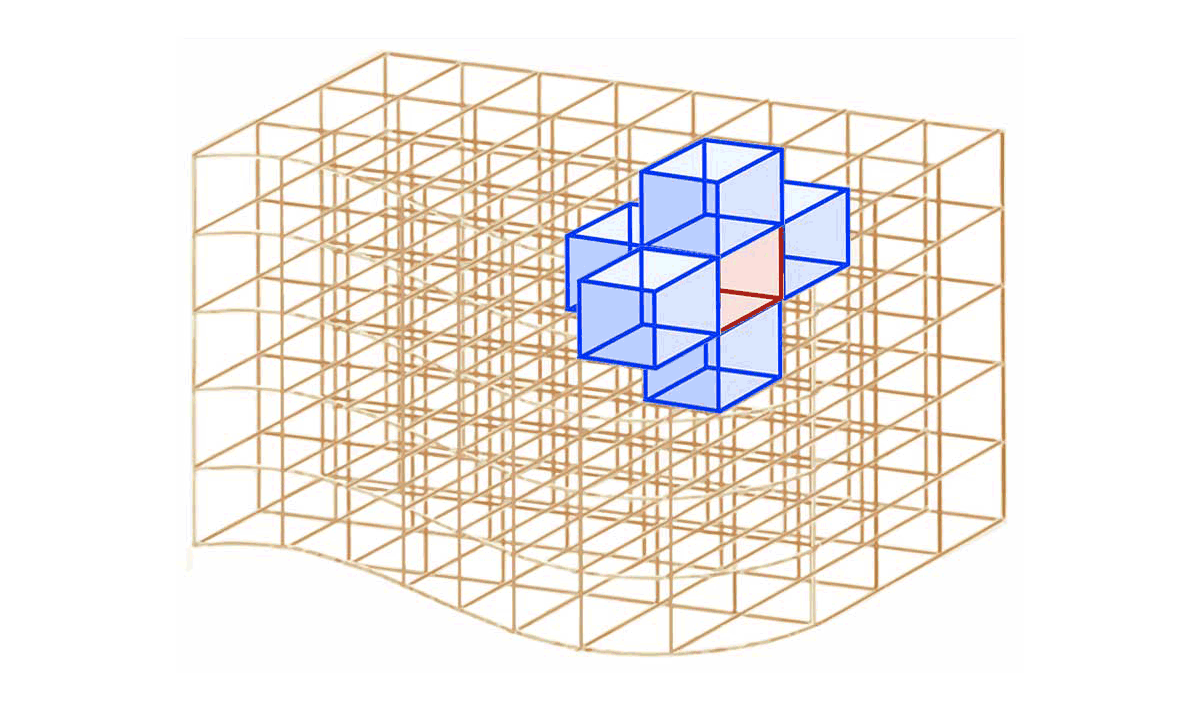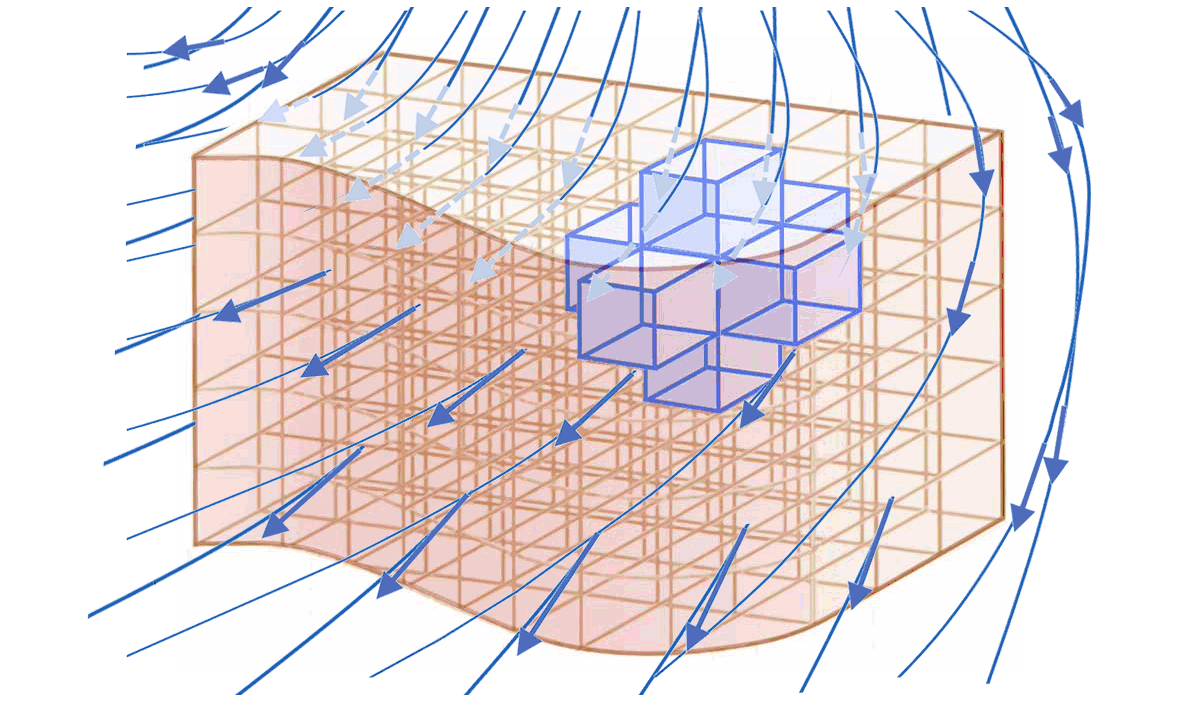
En coordonnées cartésiennes, cylindriques ou sphérique, chaque élément de surface fermée $dS$ associé à un élément de volume $d\tau$ qui n'est pas situé en surface du volume $\tau$ se décompose en 6 éléments de surface ouverte $d\Sigma_{int, i}$ situés à l'intérieur du volume $\tau$ :
$\mathbf{dS=\sum_{i=1}^6 d\Sigma_{int,i}}$
A l'intérieur du volume $\tau$, tout élément de surface ouverte $d\Sigma_{int}$ appartient à 2 élément de volume $d\tau_1$ et $d\tau_2$. Selon l'élément de volume considéré, un même élément de surface ouverte intérieure $\mathbf{d\Sigma_{int}}$ est représenté par les vecteurs $\overrightarrow{\Sigma}_{int,1}$ ou $\overrightarrow{\Sigma}_{int,2}$ qui sont opposés :
$\mathbf{\overrightarrow{\Sigma}_{int,2}=-\,\overrightarrow{\Sigma}_{int,1}}$
$\Longrightarrow$ les flux élémentaires $\mathbf{d\Phi_{int,1}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{int,1}}$ et $\mathbf{d\Phi_{int,2}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{int,2}}$ correspondants sont opposés :
$\mathbf{d\Phi_{int,2}=\,-\,d\Phi_{int,1}}$

$\Longrightarrow$ le flux $\mathbf{\Phi_{int}}$ de $\overrightarrow{X}$ à travers l'ensemble des $\overrightarrow{d\Sigma_i}$ situés à l'intérieur d'un volume (les $d\Sigma_i$ appartenant à la frontière extérieure du volume étant exclus) est nul :
$\displaystyle\mathbf{\Phi_{int}=\int d\Phi_{int}=0}$
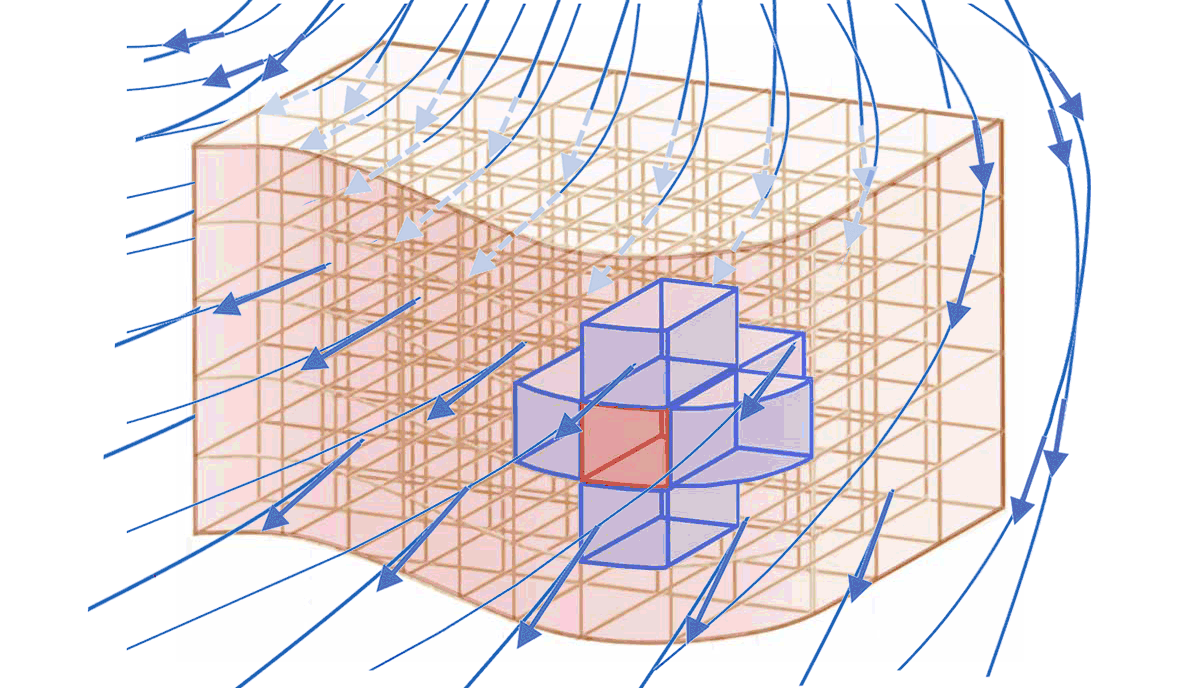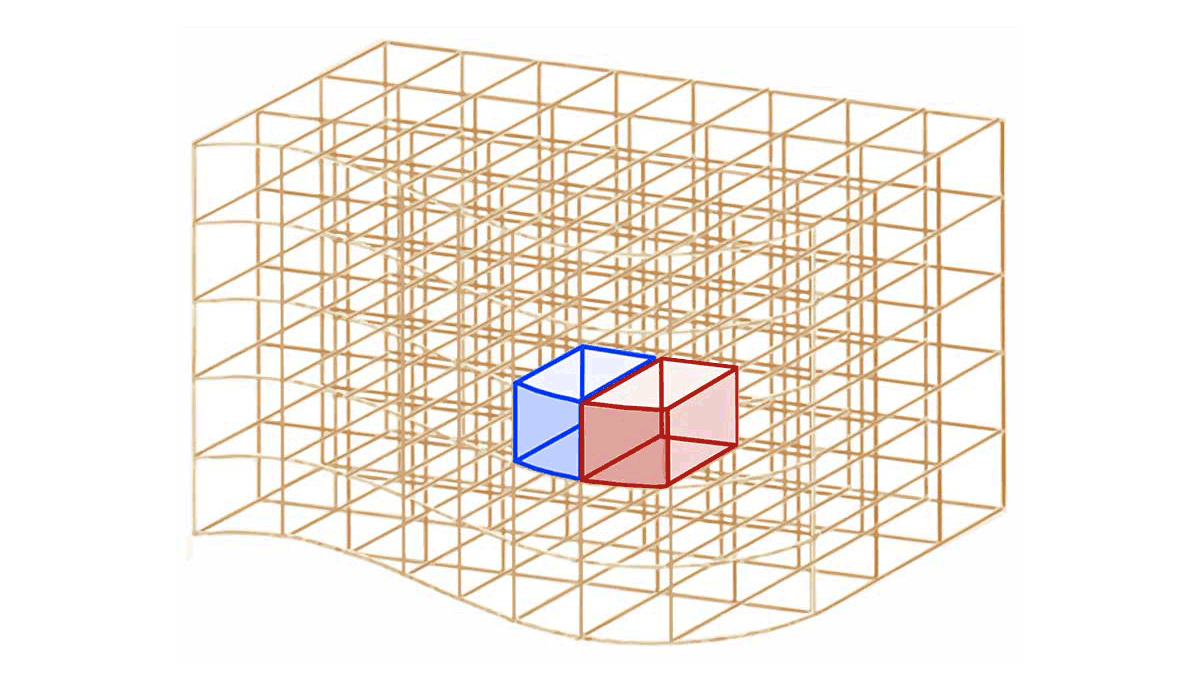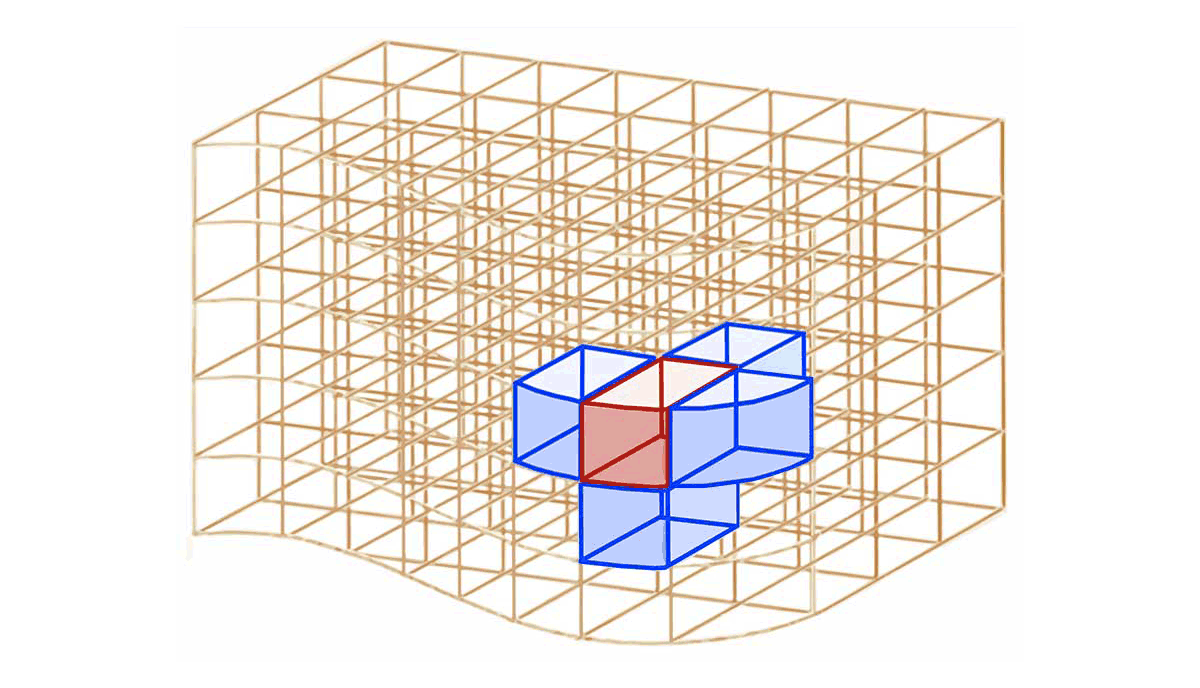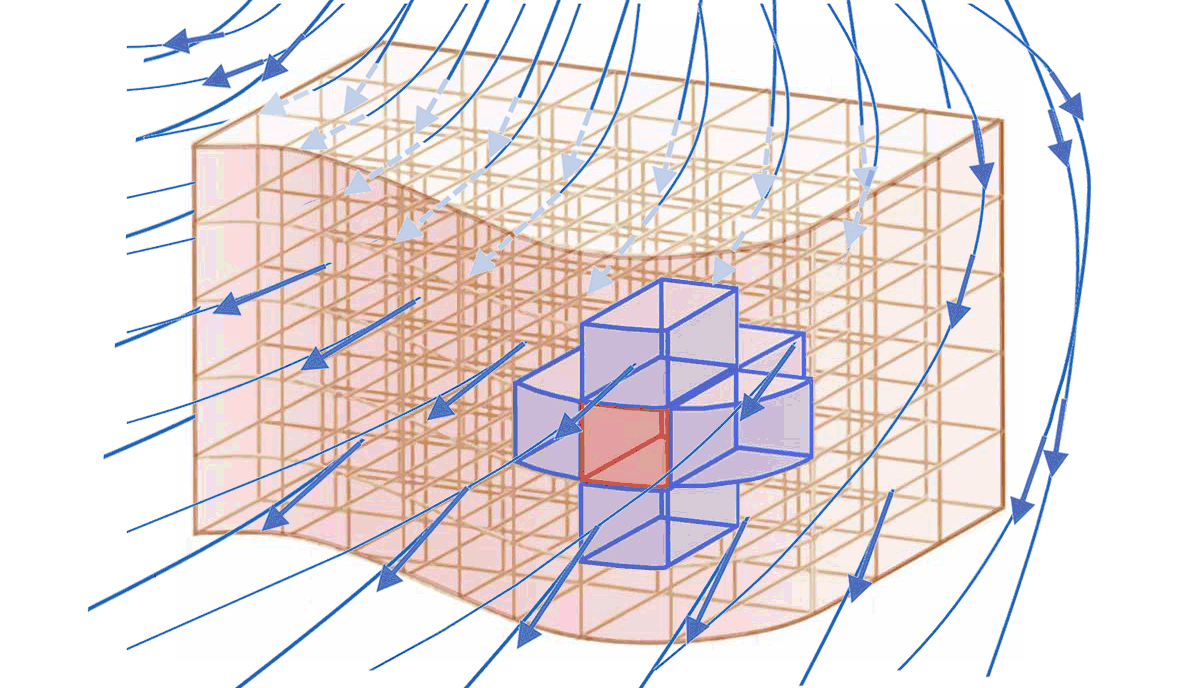
Tout élément de volume $d\tau$ en contact avec l'extérieur possède un élément de surface $d\Sigma_{ext}$. qui appartient à la frontière entre l'intérieur du volume et l'extérieur.

Tout élément de surface $d\Sigma_{ext}$ n'appartient qu'à un unique élement de volume $d\tau$ du volume $\tau$ :
$\Longrightarrow$ lui est associé un unique élément vectoriel de surface $\overrightarrow{d\Sigma}_{ext}$ orienté de l'intérieur vers l'extérieur.
$\Longrightarrow$ le flux élémentaire correspondant $d\Phi_{ext}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{ext}$ est en général non nul :
en général, $\mathbf{d\Phi_{ext}=\overrightarrow{X}\cdot \overrightarrow{d\Sigma}_{ext}}\ne 0$
L'ensemble des $d\Sigma_{ext}$ est la surface fermée $S$ délimitant le volume $\tau$ :
$S=\oiint d\Sigma_{ext}$
$\Longrightarrow$ le flux $\mathbf{\Phi_{ext}}$ de $\overrightarrow{X}$ à travers l'ensemble des $\overrightarrow{d\Sigma_{ext}}$ est le flux $\mathbf{\Phi_X}$ de $\overrightarrow{X}$ à travers la surface fermée $S$ délimitant le volume $\tau$ :
$\displaystyle\mathbf{\Phi_{ext}=\int d\Phi_{ext}=\oiint_S \overrightarrow{X}\cdot \overrightarrow{dS}}$

En résumé :
$\displaystyle\Phi_X=\int d\Phi_X=\int div\,\overrightarrow{X}\cdot \overrightarrow{d\tau}$ $\quad=\Phi_{int}+\Phi_{ext}$$\displaystyle\quad=0+\oiint_S \overrightarrow{X}\cdot \overrightarrow{dS}$
Théorème de Green-Ostrogradsky
= théorème de la divergence :

$\mathbf{\displaystyle\iiint_{\tau \leftrightarrow S} div\,\overrightarrow{X}\cdot d\tau = \oiint_{S \leftrightarrow \Ltau}\overrightarrow{X}\cdot dS}$

Que devient le théorème de Gauss exprimé localement ?

Le théorème de Gauss intégral donne : $\Phi_X=\oiint_S \overrightarrow{X}\cdot \overrightarrow{dS}=4\pi\,K\cdot \iiint \rho_X\cdot d\tau$
Le théorème de Green-Ostrogradsky donne : $\Phi_X=\oiint_{S\longleftrightarrow\Ltau} \overrightarrow{X}\cdot \overrightarrow{dS}=\iiint_{\Ltau\longleftrightarrow S} div\overrightarrow{X}\cdot d\tau$
Nous en déduisons : $\iiint_{\Ltau\longleftrightarrow S} div\overrightarrow{X}\cdot d\tau =4\pi\,K\cdot \iiint \rho_X\cdot d\tau$
L'égalité précédente étant vrai pour tout volume $\tau$, elle implique l'égalité des intégrandes qui donne le théorème de Gauss local :
$\mathbf{div\overrightarrow{X}=4\pi\,K\cdot \rho_X}$

Quelle est l'expression du théorème de Gauss local en électrostatique ?

En électrostatique : $K=\dfrac{1}{4\pi\,\epsilon_0}$, où $\rho$ est la densité volumique de charge (exprimée en $C\,m^{-3}$ dans le système international d'unités)
Théorème de Gauss local : $\large\mathbf{div\,\overrightarrow{E}=\dfrac{\rho}{\epsilon_0}}$

Quelle est l'expression du théorème de Gauss local en gravitation ?

En gravitation newtonnienne : $K=-\;G$ , où $\rho$ est la densité volumique de masse (exprimée en $kg\,m^{-3}$ dans le système international d'unités)
Théorème de Gauss local : $\large\mathbf{div\,\mathcal{\overrightarrow{G}}=-\,4\pi\,G\,\rho}$

32 KiB Raw Blame History