6.1 KiB
| title | media_order | published | routable | visible | lessons |
|---|---|---|---|---|---|
| La lente delgada | lens-divergent-N2-es.jpeg,lens-convergent-N2-en.jpeg,lens-convergent-N2-es.jpeg,lens-convergent-N2-fr.jpeg,lens-divergent-N2-en.jpeg,lens-divergent-N2-fr.jpeg | true | true | false | [slug:simple-optical-elements [{order 3}]] |
!!!! CURSO EN CONSTRUCCIÓN :
!!!! Publicado pero invisible: no aparece en la estructura de árbol del sitio m3p2.com. Este curso está en construcción, no está aprobado por el equipo pedagógico en esta etapa.
!!!! Documento de trabajo destinado únicamente al equipo pedagógico.
¿Qué es una lente?
Objectivo
-
primero : enfocar o dispersar la luz.
-
ultimate : realizar imágenes ópticas, solo o como componente en un instrumento óptico.
Principio físico
- utiliza el fenómeno de refracción, descrito por la ley de Snell-Descartes (ley de refracción)
Constitución
- hecho de vidrio, cuarzo, plástico (para el rango visible e infrarrojo y UV cercanos).
- tiene una ** simetría de revolución **.
- 2 caras pulidas perpendiculares a su eje de simetría, una o ambas están curvadas (y la mayoría de las veces la cara curva encaja en una esfera).
<! - imagen para construir: una lente delgada ->
Interés óptico : lentes delgadas
- Lente delgada: más delgado << diámetro
- Lente delgada: elemento óptico único más importante que se usa solo o en serie con la mayoría de los instrumentos ópticos: lupas, microscopios, teleobjetivos y lentes macro, cámaras, anteojos astronómicos y terrestres.
Modelización de una lente delgada rodeada de aire, gas o vacío.
¿Por qué modelizar?
- Para comprender, calcular y predecir imágenes de objetos dados por lentes delgadas.
<! - imagen cuando vemos el objeto, la lente y la imagen ->
¿Por qué rodeada de aire, un gas o el vacío?
- En la mayoría de los instrumentos ópticos, las lentes están *rodeadas de aire *.
- El aire, los gases y el vacío tienen índices de refracción cercanos a "$ 1,000 \ pm0.001$, y se pueden aproximar por *$n_{aire}=n_{gas}=n_{vacío}=1$*
$\Longrightarrow$ mismo comportamiento óptico en el aire, un gas y el vacío.
Tipos y caracterizaciones de lentes delgadas
Convergente = convexa = lente positiva
*Caracterizada por :
\ - Longitud focal (generalmente en cm) siempre> 0 + adjetivo "convergente" o
\ - Su distancia focal imagen $f '$ (en valor algebraico, generalmente en cm), que es positiva$ f'> 0 $.
o
\ - Su **vergencia ** $V$ (en oftalmología) que es positiva$ V> 0 $,
con $V (\ delta) = \dfrac{1}{f '(m)}$ ($f'$ se expresa en m "metro" y $V$ en $\delta$" dioptría", entonces $\delta=m^{-1}$)
.
Divergente = cóncava = lente negativa
- Caracterizada por:
\ - Distancia focal (generalmente en cm) siempre> 0 + adjetivo "divergente"
o
\ - Su distancia focal imagen $f '$ (en valor algebraico, generalmente en cm), que es * negativa $f'<0$*.
o
\ - Su vergencia $V$ (en oftalmología) que es negativa $V<0$,
con $V (\delta)=\dfrac{1}{f '(m)}$ ($f'$ se expresa en m "metro" y $V$ en $\delta$ "dioptría", entonces $\delta=m^{- 1}$).
Estudio analítico
(para lentes delgadas rodeadas de aire, gas o vacío)
relación de conjugación de la lente delgada
$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=V=-\dfrac{1}{\overline{OF}}=\dfrac{1}{\overline{OF'}}$
Expresión del aumento transversal
**$M_{T-thinlens}=\dfrac{\overline{OA'}}{\overline{OA}}$**
Estudio gráfico
Representación de una lente delgada
-
eje óptico = eje de revolución de la lente, orientado positivamente hacia la propagación de la luz (del objeto a la lente).
-
Representación de una lente delgada:
\ - segmento de línea, perpendicular al eje óptico, centrado en el eje con indicación simbólica de la forma de la lente en sus extremos (convexo o cóncavo).
\ - S = C = O: vértice S = punto nodal C (= centro O de una lente delgada simétrica) $\Longrightarrow$ se usa el punto O.
\ - punto O, intersección del segmento de línea con el eje óptico.
\ - *punto focal objeto F * y punto focal imagen F', posicionados en el eje óptico a distancias iguales en ambos lados del punto O ($f=-f'$) a distancias algebraicas $\overline{OF}=f$ y $\overline{OF'}=f'$.
\ - plano focal objeto (P) y plano focal imagen (P'), planos perpendiculares al eje óptico, respectivamente en los puntos $F$ y $F'$.
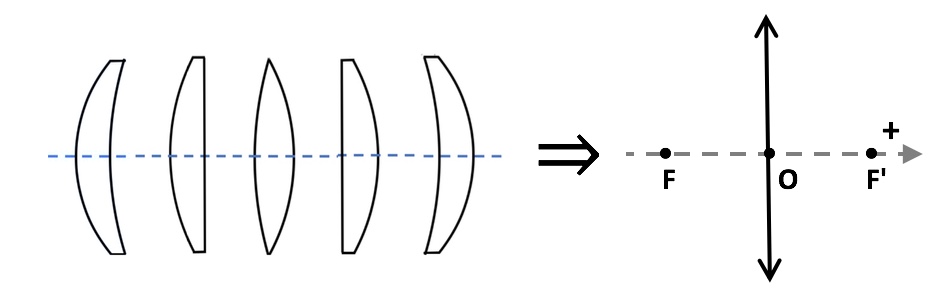
Fig. 3. Representación de una lente delgada convergente : $\overline{OF}<0$ , $\overline{OF'}>0$ et $|\overline{OF}|=|\overline{OF'}|$.
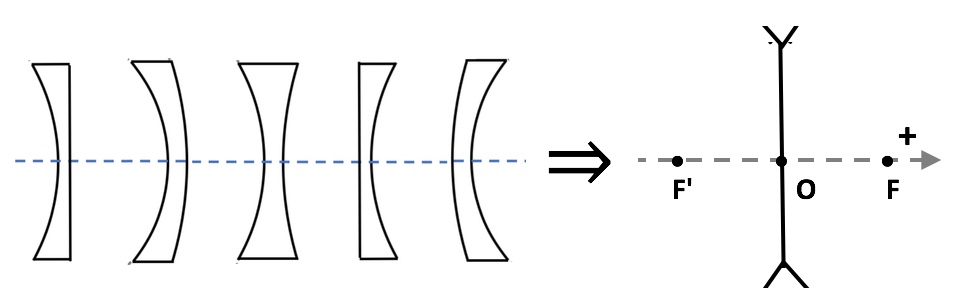
Fig. 3. Representación de una lente delgada divergente : $\overline{OF}>0$ , $\overline{OF'}<0$ et $|\overline{OF}|=|\overline{OF'}|$.
Determinación de los puntos conjugados:
Lente delgada convergente
Para animaciones geogebra:
\ - Construcción gráfica
Haga clic aquí para ver la animación
\ - Construcción gráfica y haces de luz
Haga clic aquí para ver la animación
\ - Construcción gráfica y aumento transversal
Haga clic aquí para ver la animación
- Fuente puntual localizada entre ∞ y F
- Fuente puntual localizada entre F y O
- Punto objeto virtual (se explicará a nivel cerros).
Los diferentes tipos de lentes
Modelado de una lente.
Lente delgada divergente
(para construir)






