12 KiB
| text | published | visible |
|---|---|---|
| Phénomènes d'interférences et de diffraction | false | false |
Aspect ondulatoire de la lumière
Les phénomènes d'interférences et de diffraction sont caractéristiques des ondes.
Interférences et diffraction lumineuses traduisent l'aspect ondulatoire de la lumière.
Le phénomène d'interférences
Le phénomène d'interférence est observé lorsque la superposition de deux ou plusieurs ondes de même nature (sonores, mécaniques, électro-magnétiques) donne lieu à une intensité résultante qui n'est pas égale à la simple addition des intensités prises individuellement.
!!Note : pour l'onde électromagnétique, une interférence peut se traduire localement par le phénomène : lumière + lumière = obscurité.
En pratique sur un écran d'observation, les intensités individuelles des ondes incidentes varient lentement alors que les différences de phase entre les ondes qui interfèrent et qui sont à l'origine du phénomène d'interférence varient rapidement.
On appelle franges d'interférences le lieu des points M caractérisés par une intensité moyenne $\overline{,I,}`$ donnée :
- Les franges brillantes correspondent à une intensité maximale : $
I=I_{max}$ - Les franges sombres correspondent à une intensité minimale : $
I=I_{min}$
Quantification du phénomène d'interférences : le contraste
Le contraste (ou visibilité) des franges quantifie notre aptitude à discerner les franges.
Il se définit localement à partir de la distribution d'intensité résultante des ondes qui interfèrent. Si localement $I_{max}$ est l'intensité maximum et $I_{min}$ l'intensité minimum, le contraste (ou visibilité) des franges se définit par :
$\mathcal{V} = \dfrac{I_{max}-I_{min}}{I_{max}+I_{min}}$
Cette caractérisation des franges permet une mesure comprise entre 0 et 1, valeurs limites qui représentent les deux cas extrêmes :
-
Pas de franges, donc intensité uniforme $
\Longleftrightarrow$ $I_{max}=I_{min}$ $\Longleftrightarrow$ $\mathcal{V} = 0$. -
Franges de visibilité maximum $
\Longleftrightarrow$ $I_{min}=0$ $\Longleftrightarrow$ $\mathcal{V} = 1$.
Interférences entre deux ondes électromagnétiques monochromatiques planes
Soient deux ondes planes dans le vide, notées 1 et 2, de même pulsation $\omega$ et d'amplitudes $A_1$ et $A_2$, de polarisations rectilignes selon $\overrightarrow{e_1}$ et $\overrightarrow{e_2}$, et qui se superposent en un point M de l'espace localisé, par rapport à un point pros comme origine de l'espace, par le vecteur $\overrightarrow{r} = \overrightarrow{OM}$
Ces deux ondes s'écrivent :
- Expression en notation réelle :
$\overrightarrow{E_1}(\overrightarrow{r},t) = A_1 \cdot cos (\omega t-\phi_1)\cdot \overrightarrow{e_1}$ et
$\overrightarrow{E_2}(\overrightarrow{r},t) = A_2 \cdot cos(\omega t-\phi_2)\cdot \overrightarrow{e_2}$
- Expression en notation complexe :
$\underline{\overrightarrow{E_1}}(\overrightarrow{r},t) = A_1 \cdot e^{-i\,(\omega t-\phi_1)} \cdot \overrightarrow{e_1}$ et $\underline{\overrightarrow{E_2}}(\overrightarrow{r},t) = A_2 \cdot e^{-i\,(\omega t-\phi_2)} \cdot \overrightarrow{e_2}$
! IMPORTANT :
! L'écriture réelle seule décrit la réalité de l'onde physique.
! Le champ réelle est la partie réelle du champ complexe :
$\overrightarrow{E}(\overrightarrow{r},t)= \Re \; [\underline{\overrightarrow{E}}(\overrightarrow{r},t)]$
Le champ électrique résultant est :
- Expression en notation réelle :
$\overrightarrow{E_{tot}}(\overrightarrow{r},t) = A_1 \cdot cos (\omega t-\phi_1)\cdot \overrightarrow{e_1} \;+\; A_2 \cdot cos (\omega t-\phi_2)\cdot \overrightarrow{e_2}$
- Expression en notation complexe :
$\underline{\overrightarrow{E}_{tot}}(\overrightarrow{r},t) =A_1 \; e^{-i\,\omega t} \, e^{i\,\phi_1}\cdot \overrightarrow{e_1} \;+\; A_2 \; e^{-i\,\omega t} \, e^{i\,\phi_2}\cdot \overrightarrow{e_2}$
$\underline{\overrightarrow{E}}_{tot}(\overrightarrow{r},t) = e^{-i\,\omega t} \cdot [A_1 \, e^{i\,\phi_1}\cdot \overrightarrow{e_1} + A_2 \, e^{i\,\phi_2}\cdot \overrightarrow{e_2}]$
L'intensité de l'onde résultante $I_{tot}$ s'écrit :
$\langle I_{tot} \rangle= \epsilon_0 \,c \; ||\overrightarrow{E}||^2=\dfrac{\epsilon_0\,c}{2} \; ||\overrightarrow{E}||$
- Calcul en notation réelle :
$I_{tot}= \dfrac{\epsilon_0\,c}{2} \; [A_1^2 \cdot cos^2 (\omega t-\phi_1)\cdot \overrightarrow{e_1} \cdot \overrightarrow{e_1}$ $\;+\;A_2^2 \cdot cos^2 (\omega t-\phi_2)\cdot \overrightarrow{e_2} \cdot \overrightarrow{e_2}$ $\;+\;2 \;A_1\,A_2 \cdot cos (\omega t-\phi_1)\,cos (\omega t-\phi_2)\cdot \overrightarrow{e_1} \cdot \overrightarrow{e_2}]$
- Calcul en notation complexe :
$I_{tot} = \dfrac{\epsilon_0\,c}{2} \; ||\overrightarrow{E}|| = \dfrac{\epsilon_0\,c}{2} \; \overrightarrow{E}\cdot \overrightarrow{E^*} = A_1^2\,\overrightarrow{e_1} \cdot \overrightarrow{e_1} + A_2^2\,\overrightarrow{e_2} \cdot \overrightarrow{e_2}+2 \,A_1 \, A_2\; \overrightarrow{e_1} \cdot \overrightarrow{e_2}$
$\quad\quad = A_1^2\,\overrightarrow{e_1} \cdot \overrightarrow{e_1} + A_2^2\,\overrightarrow{e_2} \cdot \overrightarrow{e_2} + \,A_1 \, A_2\;e^{i(\phi_1-\phi_2)} \;\overrightarrow{e_1} \cdot \overrightarrow{e_2} + \,A_2 \, A_1\;e^{i(\phi_2-\phi_1)} \;\overrightarrow{e_2} \cdot \overrightarrow{e_1}$
- Si les deux ondes ont des polarisations rectilignes orthogonales $
(\overrightarrow{e_1} \perp \overrightarrow{e_2})$, alors
$I_{tot}= A_1^2\,\overrightarrow{e_1} \cdot \overrightarrow{e_1} + A_2^2\,\overrightarrow{e_2} \cdot \overrightarrow{e_2}=I_1 + I_2$
Il n'y a pas interférence entre ces deux ondes.
- Si les deux ondes ont des polarisations rectilignes non orthogonales $
(\overrightarrow{e_1} \cdot \overrightarrow{e_2}) =cos \Phi$, telles que , alors
$I_{tot}=A_1^2\,\overrightarrow{e_1} \cdot \overrightarrow{e_1}+A_2^2\,\overrightarrow{e_2} \cdot \overrightarrow{e_2}+2 \,A_1\,A_2\,cos(\phi_1 - \phi_2)=I_1 + I_2 + \,2\,\sqrt{I_1\,I_2} \, cos(\phi_1 - \phi_2) \cdot cos \Phi$
Un terme d'interférence $\,2\,\sqrt{I_1\,I_2} \, cos(\phi_1 - \phi_2) \cdot cos \Phi$ apparait.
- Si les deux ondes ont des polarisations rectilignes dans la même direction $
(\overrightarrow{e_1} = \overrightarrow{e_2})$ alors $cos\, \Phi = 1$ et :
$I_{tot}= A_1^2\,\overrightarrow{e_1} \cdot \overrightarrow{e_1}+A_2^2\,\overrightarrow{e_2} \cdot \overrightarrow{e_2}+2 \,A_1\,A_2\,cos(\phi_1 - \phi_2)=I_1 + I_2 + \,2\,\sqrt{I_1\,I_2} \, cos(\phi_1 - \phi_2)$
Le terme d'interférence se limite à $\,2\,\sqrt{I_1\,I_2} \, cos(\phi_1 - \phi_2)$.
- Si les deux ondes ont une même amplitude $
A$ et des polarisations rectilignes dans la même direction $(\overrightarrow{e_1} = \overrightarrow{e_2})$ alors :
$I_{tot}=A^2\,\overrightarrow{e_1} \cdot \overrightarrow{e_1}+A^2\,\overrightarrow{e_2} \cdot \overrightarrow{e_2}+2 \,A^2\,cos(\phi_1 - \phi_2)=2 \;I \cdot [\,1+ cos(\phi_1 - \phi_2)]$
Ce sont les meilleures conditions de réalisation et d'observation.
L'interférence est :
- totalement destructive en tous les point de l'espace où les deux ondes sont en opposition de phases, soit :
$|\phi_1 - \phi_2|=(2n+1)\,\pi$ avec $n \in \mathbb{Z}$ $\Longrightarrow cos(\phi_1 - \phi_2)=-1$
En ces points là * $I_{tot}=I_{min}=0$* , l'*intensité est nulle* et donc l'obscurité totale.
- totalement constructive en tous les point de l'espace où les deux ondes sont en phase, soit :
$|\phi_1 - \phi_2|=2n\,\pi$, avec $n \in \mathbb{Z} $ $\Longrightarrow cos(\phi_1 - \phi_2)=+1$
En ces points là, $I_{tot}=I_{max}= 4 \,A^2$.
Interférences par N ondes de même amplitude, déphasés avec un pas constant
Soient N ondes de même amplitude $A$ déphasées entre-elles d'un pas constant $\phi$.
$A_{tot}=A\,e^0\,+\,A\,e^{i\phi}\,+\,A\,e^{i\phi}\,+\,\cdot\cdot\cdot\,+\,A\,e^{i\,(N-1)\,\phi}$
$\quad =A\,\cdot \,(1 \,+\,e^{i\phi}\,+\,e^{i\phi}\,+\,\cdot\cdot\cdot\,+\,e^{i\,(N-1)\,\phi})$
Le terme entre parenthèse forment une progression géométrique de raison $e^{i\phi}$.
La somme $S_N$ des termes d'une suite géométrique de premier terme $a$ et de raison $q$ avec $q \ne 0$ et $q \ne 1$ s'écrit :
$S_N=a + a\,q + a\,q^2 + a\,q^3 + \cdot\cdot\cdot + a\,q^{N-1}$
donc
$q\,S_N= a\,q + a\,q^2 + a\,q^3 + a\,q^4 + \cdot\cdot\cdot + a\,q^N$
et
$q\,S_N-S_N= a\,q^N \,- a$
$S_N\,(q-1)= a\,(q^N-1)$
$S_N=a \cdot \dfrac{q^N-1}{q-1}$
Si j'applique ce résultat concernant les suites géométriques pour calculer le terme d'amplitude totale résultantes de la superposition des ondes considérées, j'obtiens
$\underline{A_{tot}}=A\cdot \dfrac{e^{i\,N\,\phi}-1}{e^{i\,\phi}-1}=\dfrac{(1-cos\,N\phi)+i\,sin\, N\phi}{(1-cos\,\phi)+i\,sin\,\phi}$
L'intensité résultante est alors
$I_{tot}=\underline{A_{tot}}\,\underline{A^*_{tot}}=|\,A^2\,|=A^2\cdot\dfrac{(1-cos^2\,N\phi)+sin^2\,N\phi}{(1-cos^2\,\phi)+sin^2\,\phi}$
$\quad=A^2\cdot\dfrac{1-2\cos\,N\phi+cos^2\,N\phi+sin^2\,N\phi}{1-2\cos\,\phi+cos^2\,\phi+sin^2\,\phi}= A^2\cdot\dfrac{2-2\cos\,N\phi}{2-2\cos\,\phi}$
$\quad= A^2\cdot\dfrac{1-cos\,N\phi}{1-cos\,\phi}$
Avec les relations trigonométriques
$cos(a-b)=cos\,a \;cos\,b \;+\; sin\,a \;sin\,b $
$cos(a+b)=cos\,a \;cos\,b \;-\; sin\,a \;sin\,b $
j'obtiens
$cos(a-b)-cos(a+b)=2\; sin\,a \;sin\,b $
L'identification $a=b=\dfrac{N\,\phi}{2}$ conduit à
$cos\left(\dfrac{N\,\phi}{2}-\dfrac{N\,\phi}{2}\right)-cos\left(\dfrac{N\,\phi}{2}+\dfrac{N\,\phi}{2}\right)=2\; sin\,\dfrac{N\,\phi}{2} \;sin\,\dfrac{N\,\phi}{2} $
$cos\,0 - cos\,N\,\phi=1 - cos\,N\,\phi =2\; sin^2\,\dfrac{N\,\phi}{2}$
De même, l'identification $=b=\dfrac{\phi}{2}$ conduit à $1 - cos\,\phi =2\; sin^2\,\dfrac{\phi}{2}$ .
Au total, la distribution d'intensité en fonction du pas de déphasage $\phi$ entre deux rayons consécutifs s'écrit :
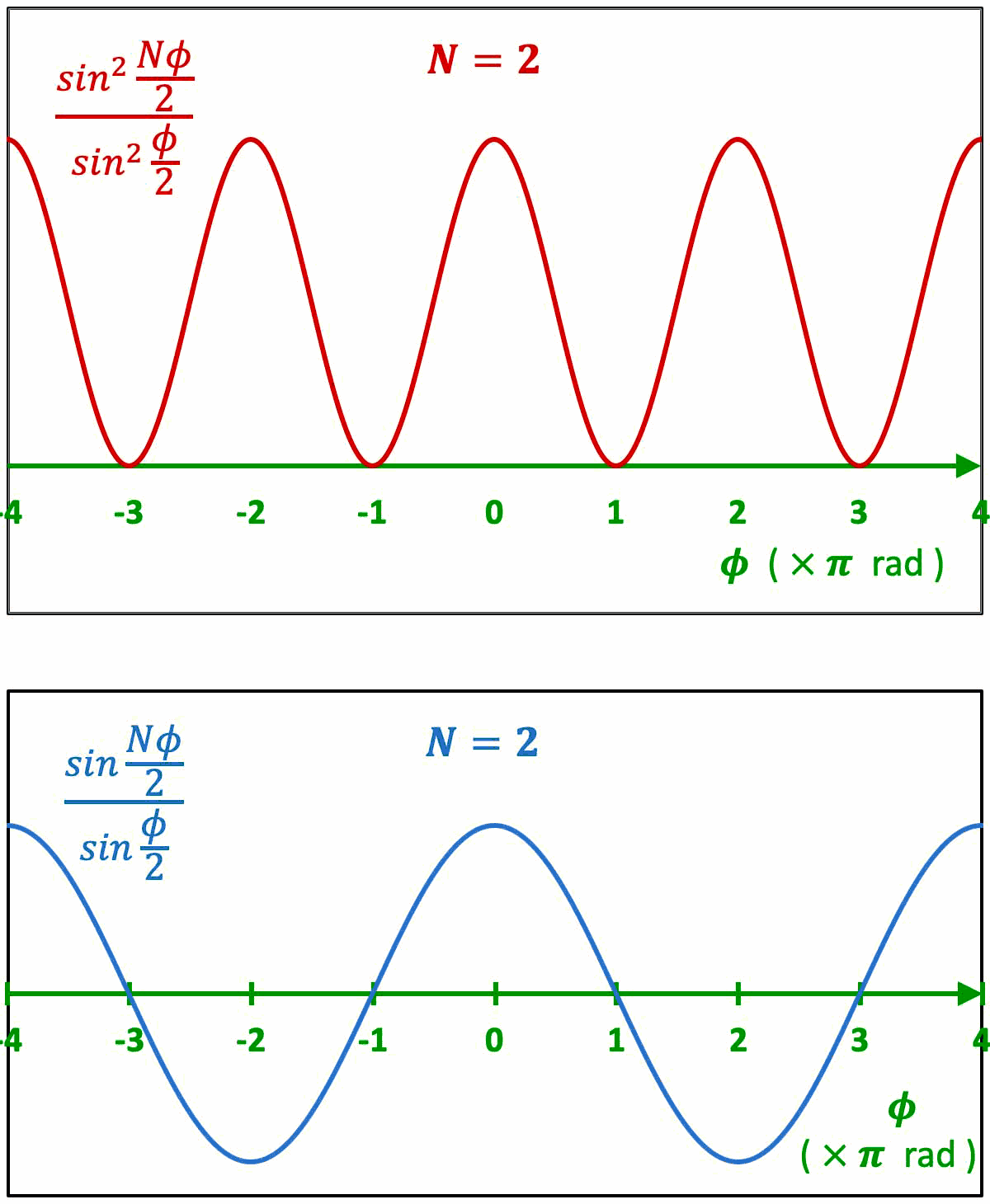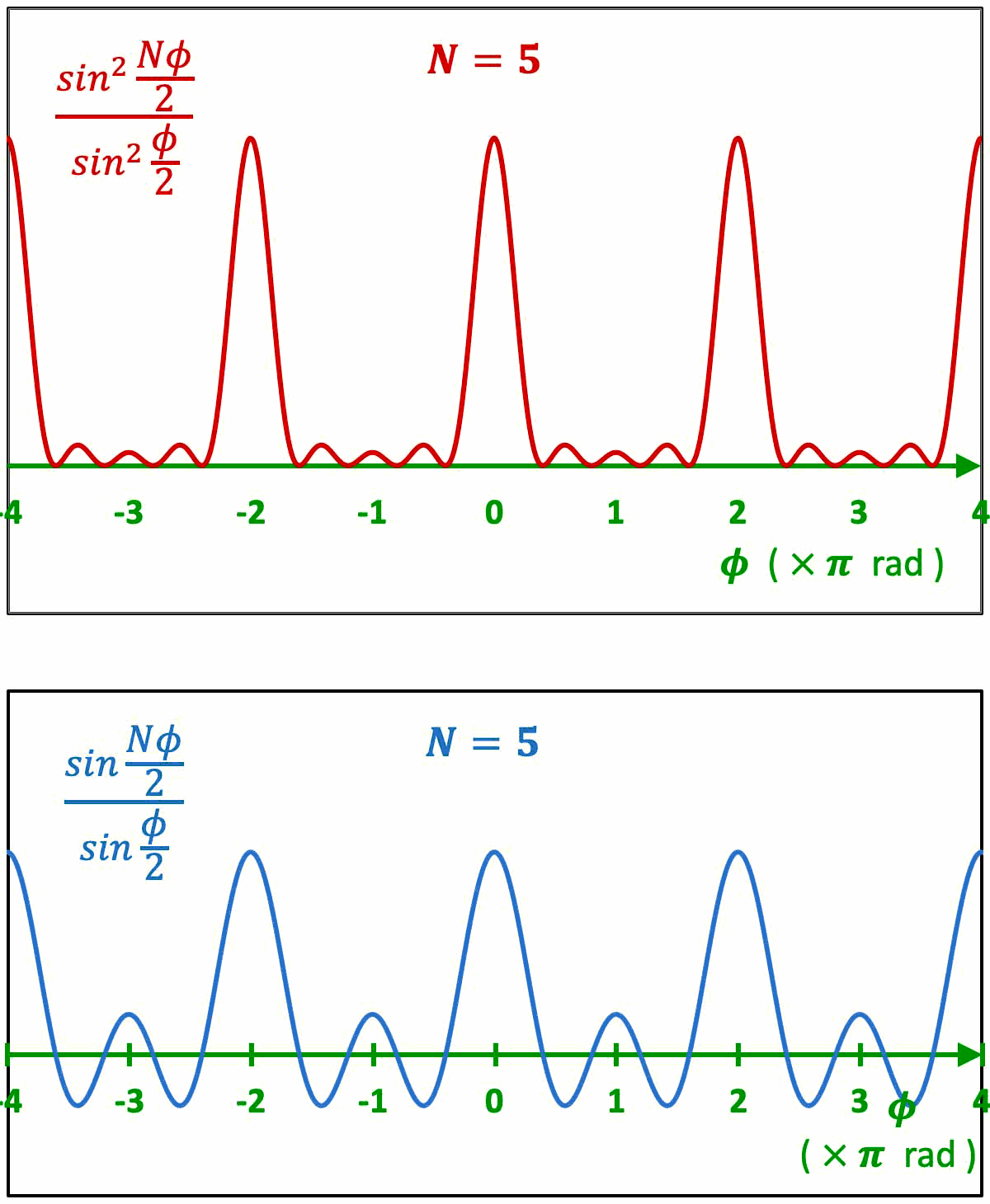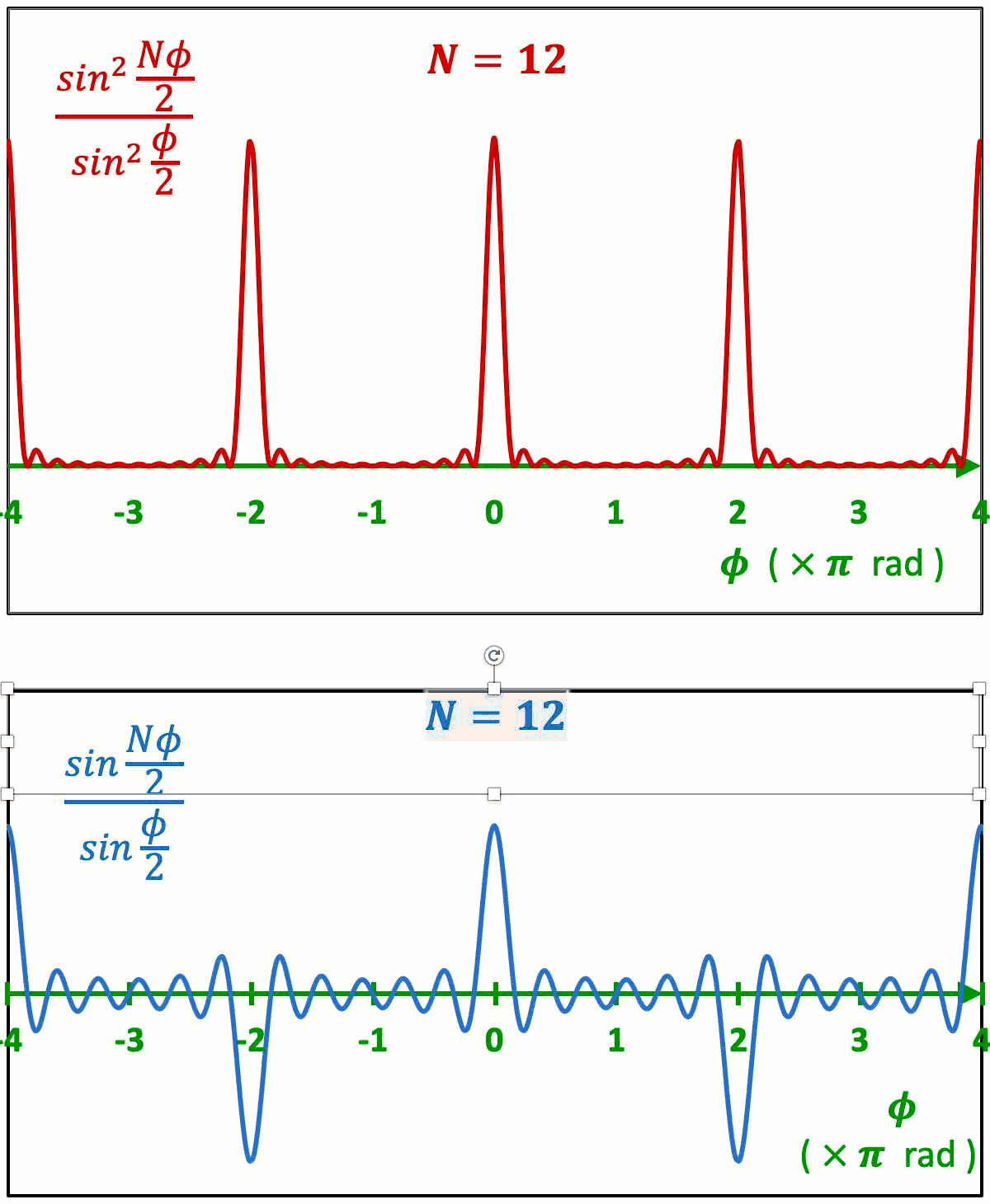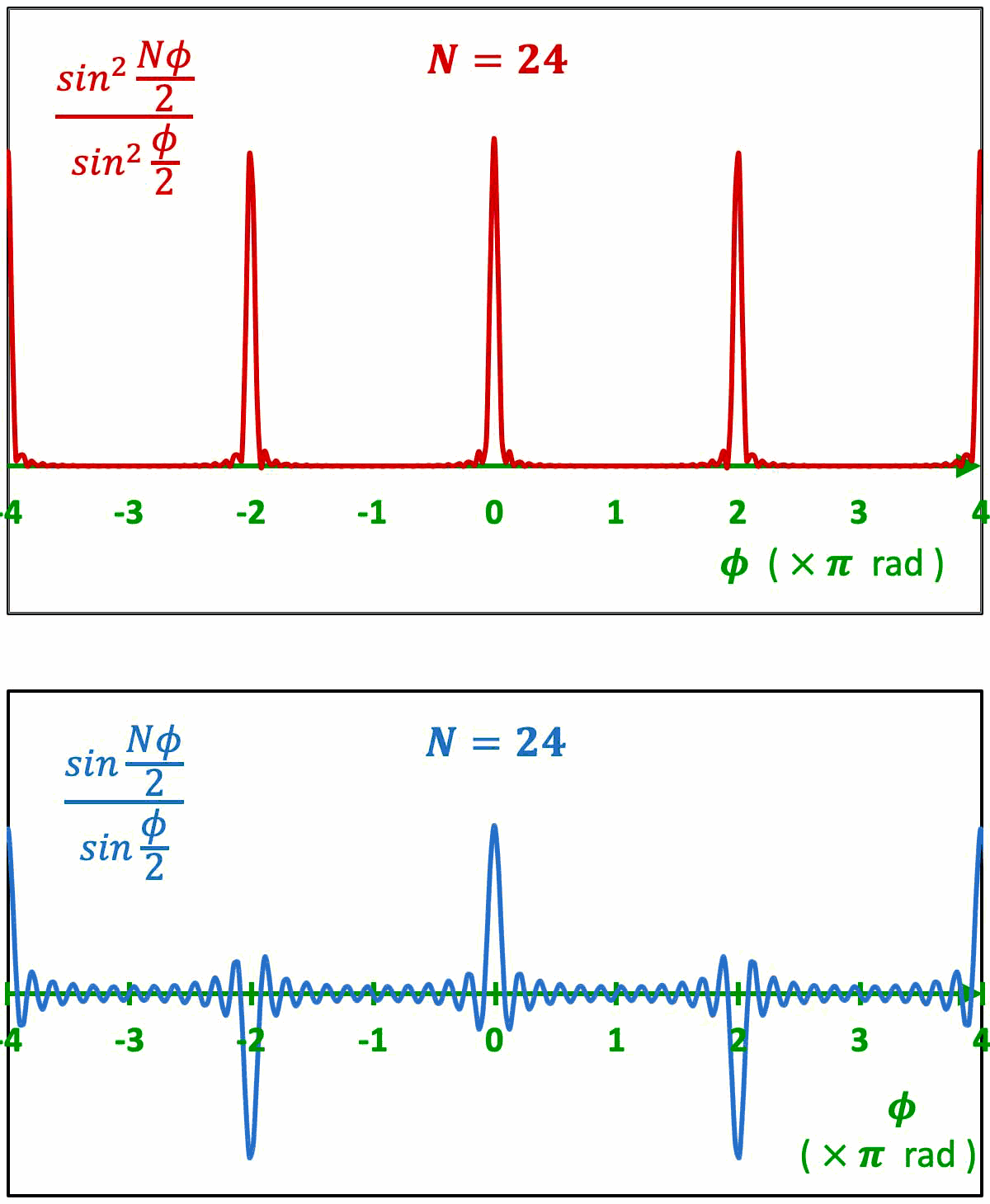
$I_{tot}= A^2\cdot\dfrac{sin^2\,\dfrac{N\,\phi}{2}}{sin^2\,\dfrac{\phi}{2}}$
Cette fonction $\dfrac{sin^2\,\dfrac{N\,\phi}{2}}{sin^2\,\dfrac{\phi}{2}}$ est la fonction très importante dans l'étude et le calcul des phénomènes d'interférences.
J'étudie analytiquement cette fonction
-
Quelle est sa valeur en $
\phi=0$ ? -
Pour quelles valeurs de $
\phi$ l'intensité s'annule-t-elle totalement ?
Et questions de compréhension qualitative :
-
Que se passe-t-il si les ondes qui interfèrent n'ont pas la même amplitude ?
-
Que se passe-t-il si les ondes EM qui interfèrent sont polarisées rectilignement, mais toutes dans des directions différentes ?
Je visualise cette fonction
-
$
N=1 \Longrightarrow$ amplitude et intensité de l'onde uniforme : pas d'interférences. -
$
N=2 \Longrightarrow$ amplitude set intensité de l'onde uniforme : interférences à deux ondes.
Faisons croître le nombre $N$ des ondes qui interfèrent, et observons :
Pour prendre un peu d'avance :
Après l'études des phénomènes d'interférences et de diffraction, je regarderai quelques situations physiques simples ou quelques éléments optiques qui réalisent ces phénomènes. Le cours se construit.
Mais déjà, je verrai qu'une façon d'obtenir de telles interférences est d'illuminer un réseau de diffraction avec une onde (je préciserai les conditions).
Dans ce cas, lors de l'observation de la lumière à l'infini dans une direction donnée, la différence de phase $\phi$ entre deux ondes est fonction de la longueur d'onde selon l'expression :
$\phi=\dfrac{2 \pi \, \delta}{\lambda}$.
Deux longueurs d'onde différentes donneront deux systèmes de franges différentes, qui se superposeront.
Je regarde bien les figures suivantes, pour comprendre visuellement le phénomène observé. Cela donne une première piste pour décomposer une lumière polychromatique en ses différentes composantes.
Et une première compréhension des ordres de travail d'un réseau de diffraction :