5.7 KiB
| title | media_order | published | visible |
|---|---|---|---|
| La lente delgada | lens-divergent-N2-es.jpeg,lens-convergent-N2-en.jpeg,lens-convergent-N2-es.jpeg,lens-convergent-N2-fr.jpeg,lens-divergent-N2-en.jpeg,lens-divergent-N2-fr.jpeg | true | true |
La vergencia de una lente
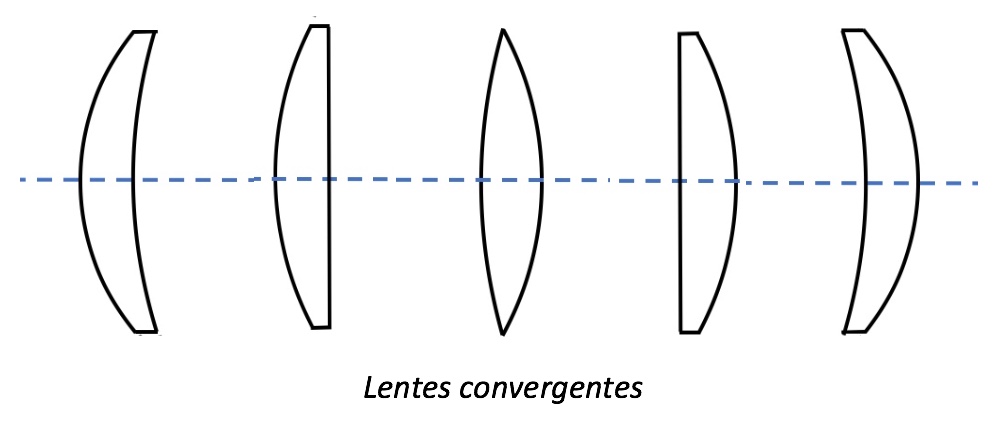
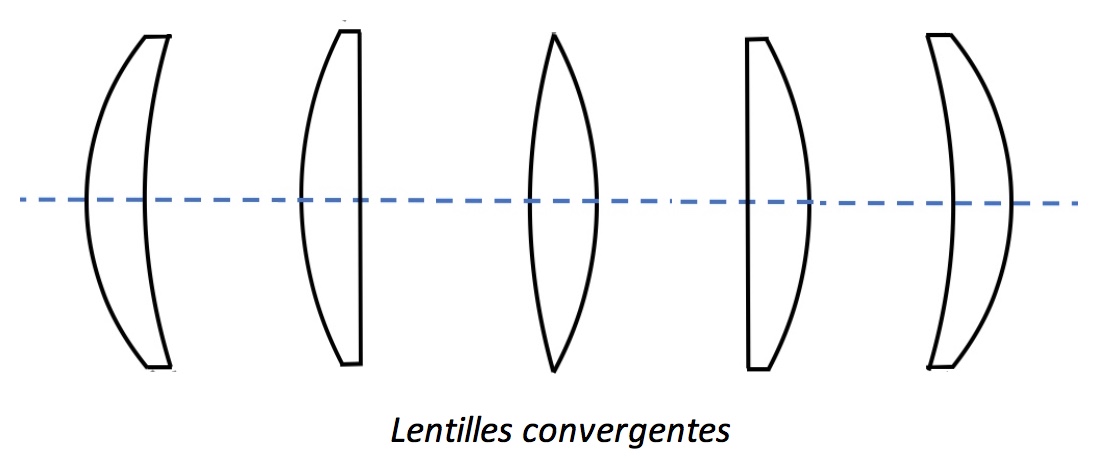
Los diferentes tipos de lentes
Modelado de una lente.
¿Qué es una lente?
Objectivo
-
primero : enfocar o dispersar la luz.
-
ultimate : realizar imágenes ópticas, solo o como componente en un instrumento óptico.
Principio físico
- utiliza el fenómeno de refracción, descrito por la ley de Snell-Descartes (ley de refracción)
Constitución
- hecho de vidrio, cuarzo, plástico (para el rango visible e infrarrojo y UV cercanos).
- tiene una ** simetría de revolución **.
- 2 caras pulidas perpendiculares a su eje de simetría, una o ambas están curvadas (y la mayoría de las veces la cara curva encaja en una esfera).
<! - imagen para construir: una lente delgada ->
Interés óptico : lentes delgadas
- Lente delgada: más delgado << diámetro
- Lente delgada: elemento óptico único más importante que se usa solo o en serie con la mayoría de los instrumentos ópticos: lupas, microscopios, teleobjetivos y lentes macro, cámaras, anteojos astronómicos y terrestres.
Modelización de una lente delgada rodeada de aire, gas o vacío.
¿Por qué modelizar?
- Para comprender, calcular y predecir imágenes de objetos dados por lentes delgadas.
<! - imagen cuando vemos el objeto, la lente y la imagen ->
¿Por qué rodeada de aire, un gas o el vacío?
- En la mayoría de los instrumentos ópticos, las lentes están *rodeadas de aire *.
- El aire, los gases y el vacío tienen índices de refracción cercanos a "$ 1,000 \ pm0.001$, y se pueden aproximar por *$n_{aire}=n_{gas}=n_{vacío}=1$*
$\Longrightarrow$ mismo comportamiento óptico en el aire, un gas y el vacío.
Tipos y caracterizaciones de lentes delgadas
Convergente = convexa = lente positiva
*Caracterizada por :
\ - Longitud focal (generalmente en cm) siempre> 0 + adjetivo "convergente" o
\ - Su distancia focal imagen $f '$ (en valor algebraico, generalmente en cm), que es positiva$ f'> 0 $.
o
\ - Su **vergencia ** $V$ (en oftalmología) que es positiva$ V> 0 $,
con $V (\ delta) = \dfrac{1}{f '(m)}$ ($f'$ se expresa en m "metro" y $V$ en $\delta$" dioptría", entonces $\delta=m^{-1}$)
.
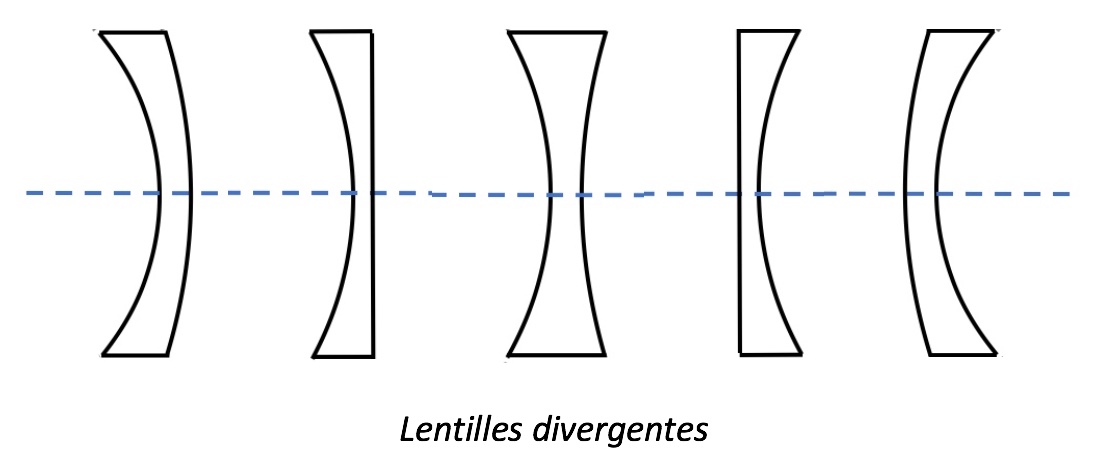
Divergente = cóncava = lente negativa
- Caracterizada por:
\ - Distancia focal (generalmente en cm) siempre> 0 + adjetivo "divergente"
o
\ - Su distancia focal imagen $f '$ (en valor algebraico, generalmente en cm), que es * negativa $f'<0$*.
o
\ - Su vergencia $V$ (en oftalmología) que es negativa $V<0$,
con $V (\delta)=\dfrac{1}{f '(m)}$ ($f'$ se expresa en m "metro" y $V$ en $\delta$ "dioptría", entonces $\delta=m^{- 1}$).
Estudio analítico
(para lentes delgadas rodeadas de aire, gas o vacío)
relación de conjugación de la lente delgada
$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=V=-\dfrac{1}{\overline{OF}}=\dfrac{1}{\overline{OF'}}$
Expresión del aumento transversal
**$M_{T-thinlens}=\dfrac{\overline{OA'}}{\overline{OA}}$**
Estudio gráfico
Representación de una lente delgada
-
eje óptico = eje de revolución de la lente, orientado positivamente hacia la propagación de la luz (del objeto a la lente).
-
Representación de una lente delgada:
\ - segmento de línea, perpendicular al eje óptico, centrado en el eje con indicación simbólica de la forma de la lente en sus extremos (convexo o cóncavo).
\ - S = C = O: vértice S = punto nodal C (= centro O de una lente delgada simétrica) $\Longrightarrow$ se usa el punto O.
\ - punto O, intersección del segmento de línea con el eje óptico.
\ - *punto focal objeto F * y punto focal imagen F', posicionados en el eje óptico a distancias iguales en ambos lados del punto O ($f=-f'$) a distancias algebraicas $\overline{OF}=f$ y $\overline{OF'}=f'$.
\ - plano focal objeto (P) y plano focal imagen (P'), planos perpendiculares al eje óptico, respectivamente en los puntos $F$ y $F'$.

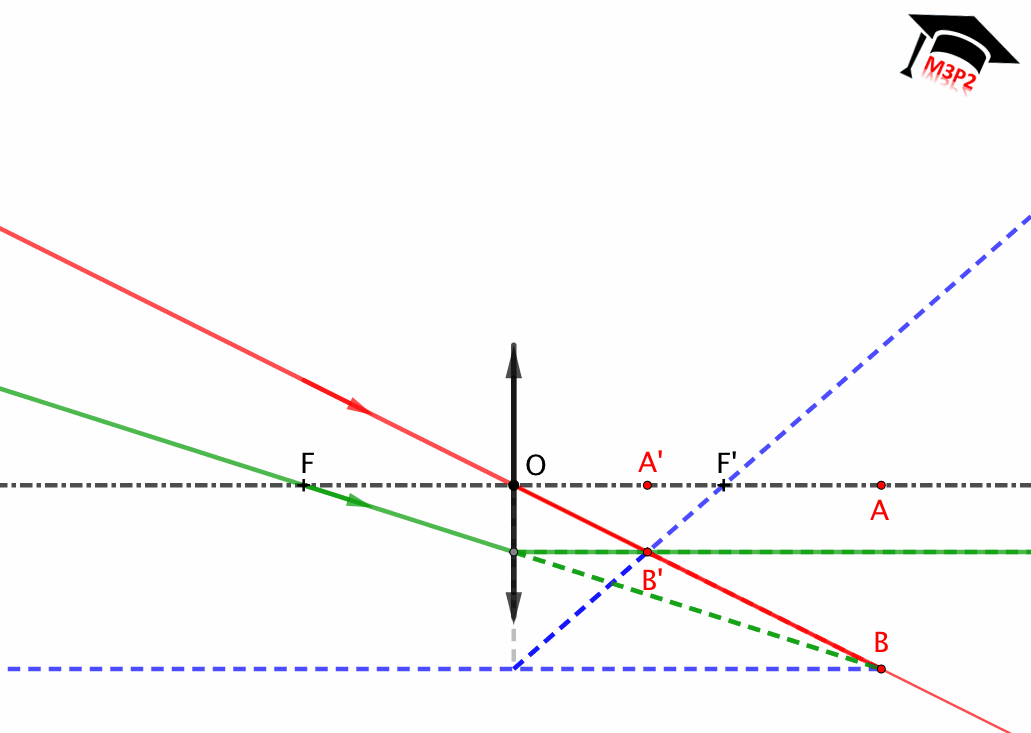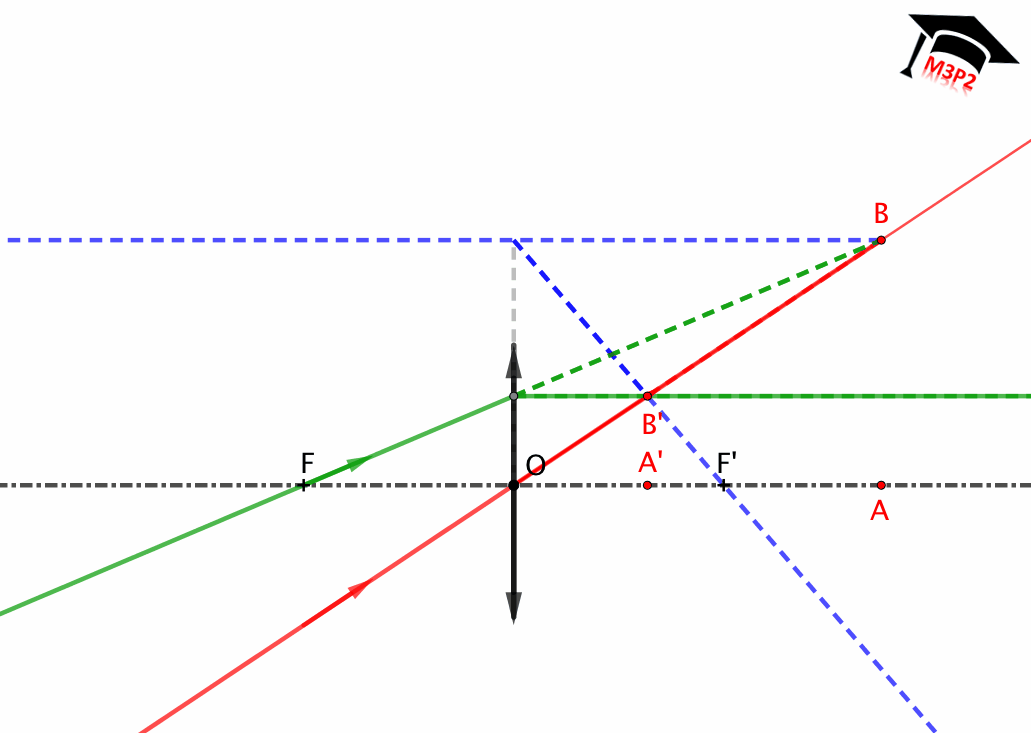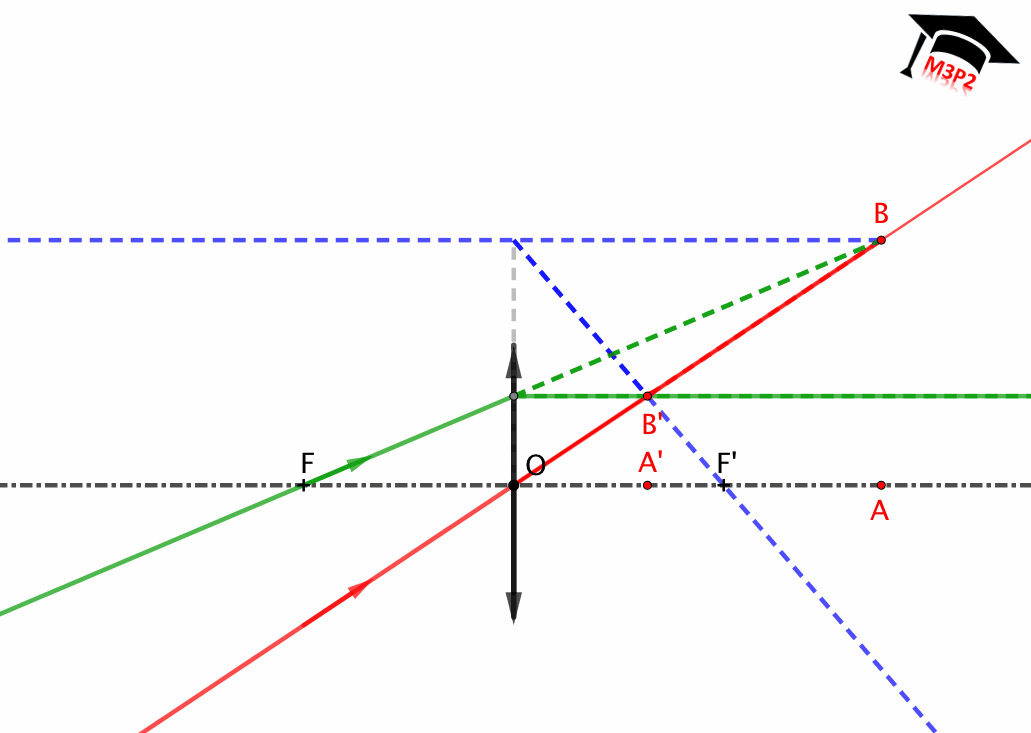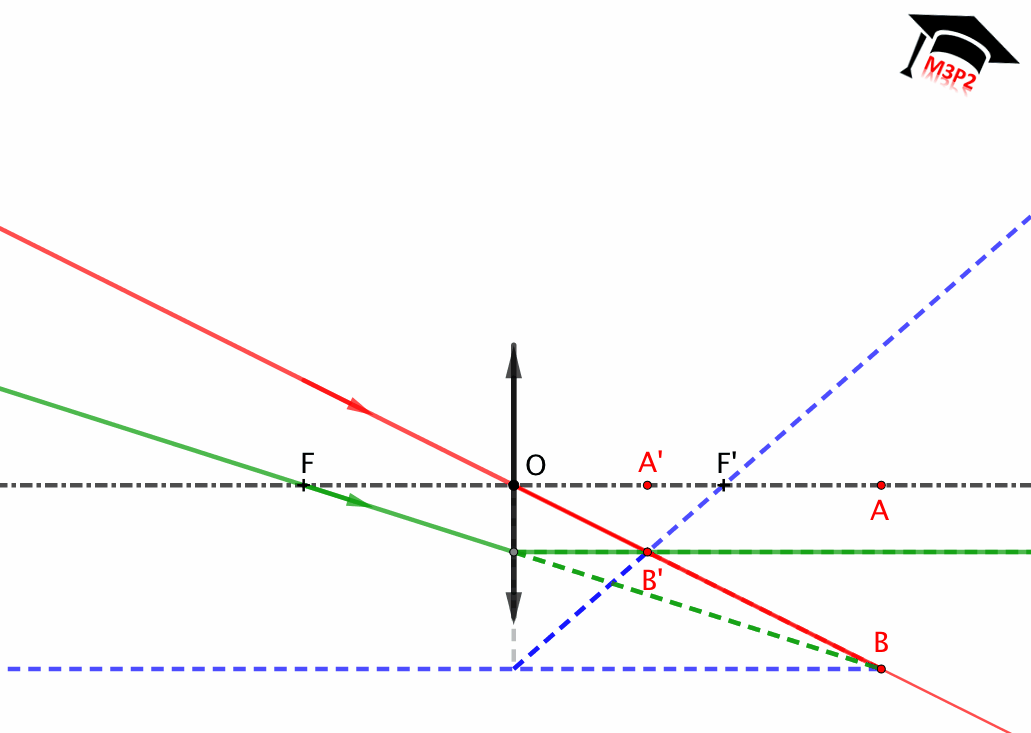
Fig. 3. Representación de una lente delgada convergente : $\overline{OF}<0$ , $\overline{OF'}>0$ et $|\overline{OF}|=|\overline{OF'}|$.

Fig. 3. Representación de una lente delgada divergente : $\overline{OF}>0$ , $\overline{OF'}<0$ et $|\overline{OF}|=|\overline{OF'}|$.
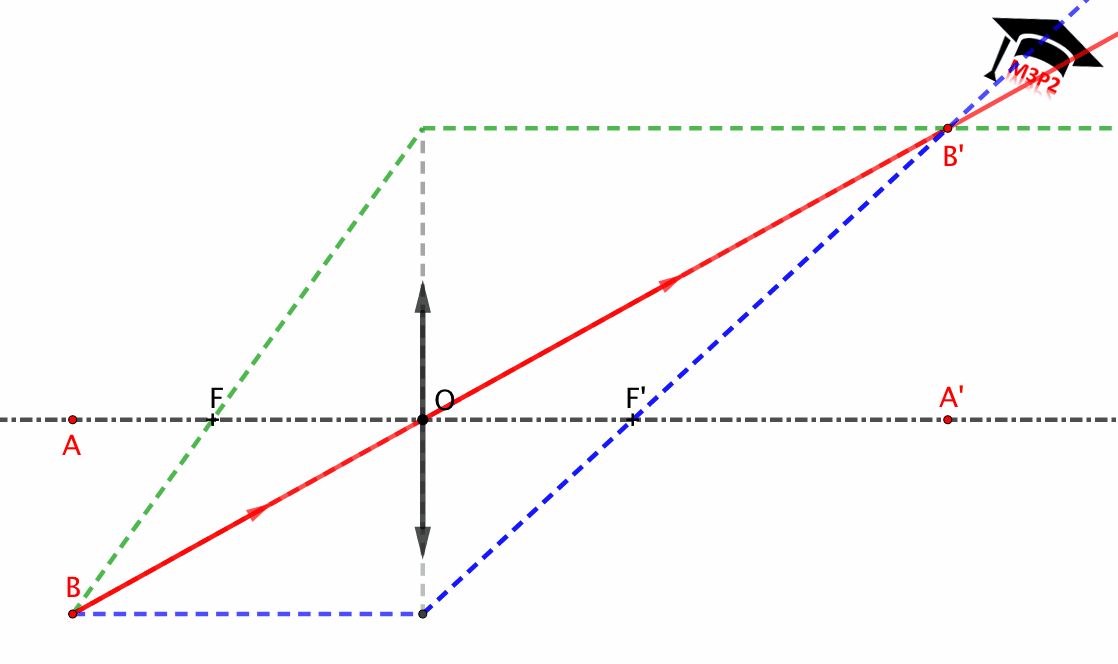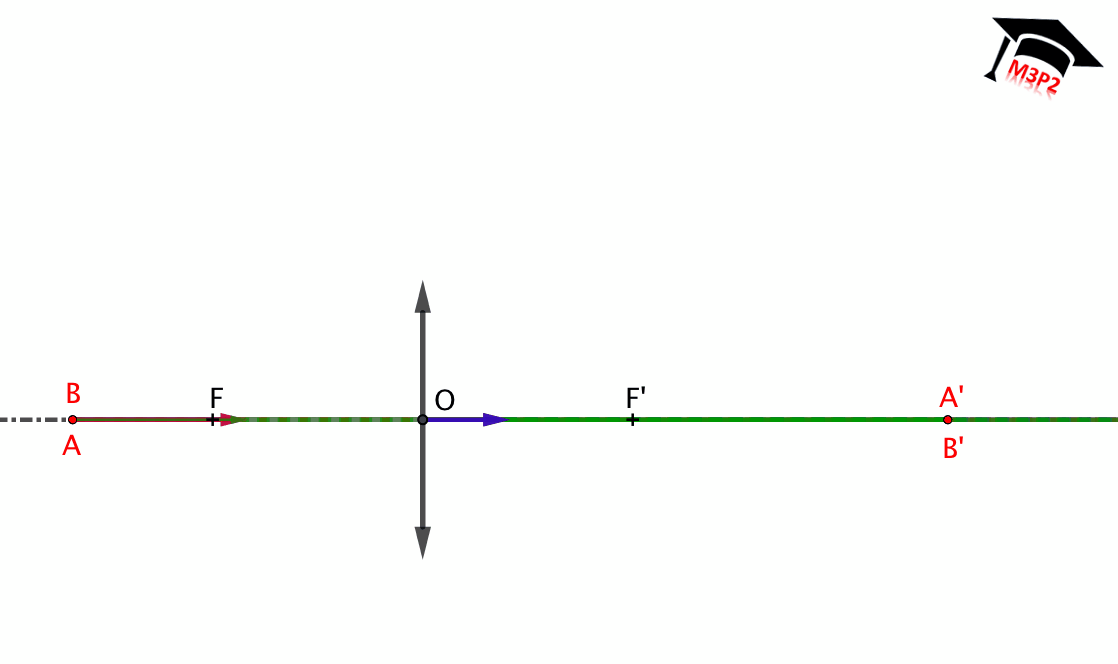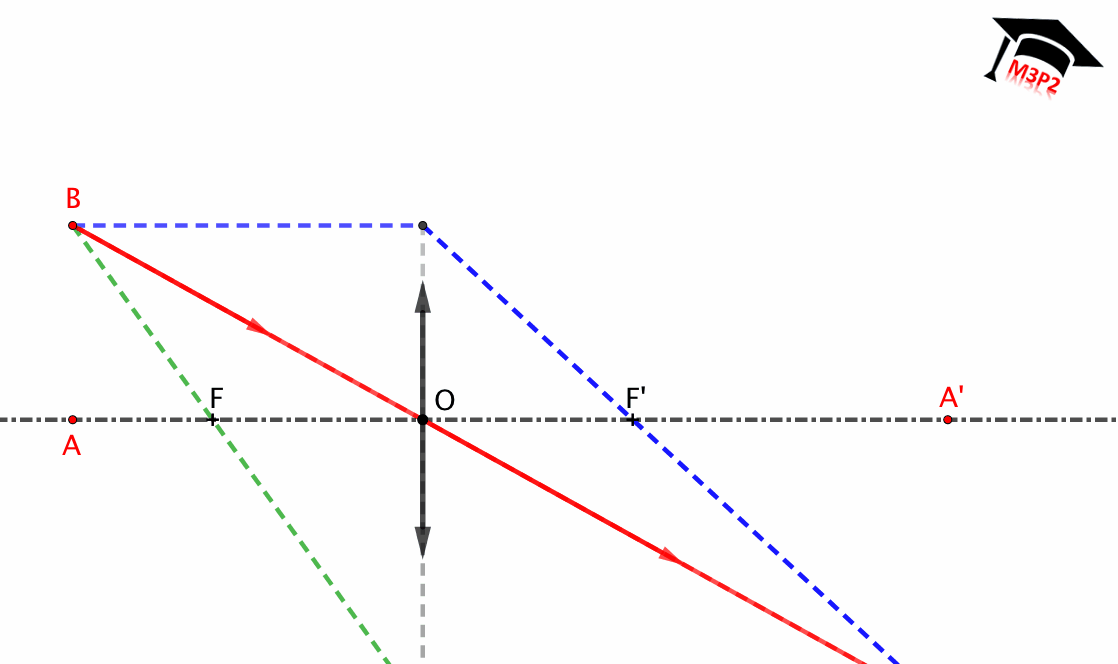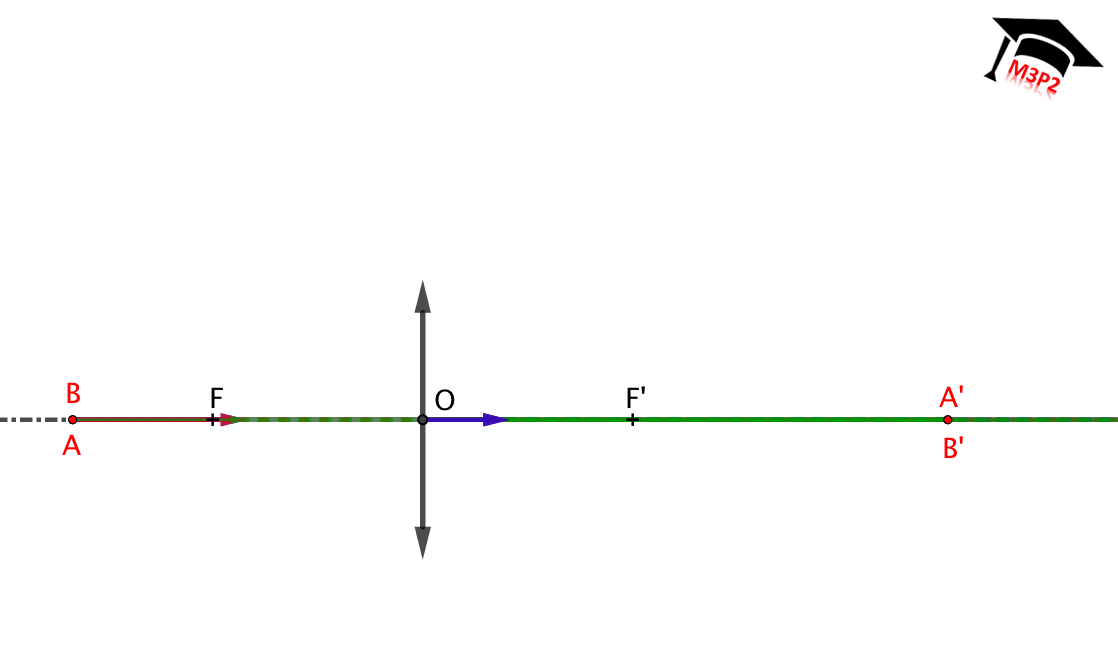
Determinación de los puntos conjugados:
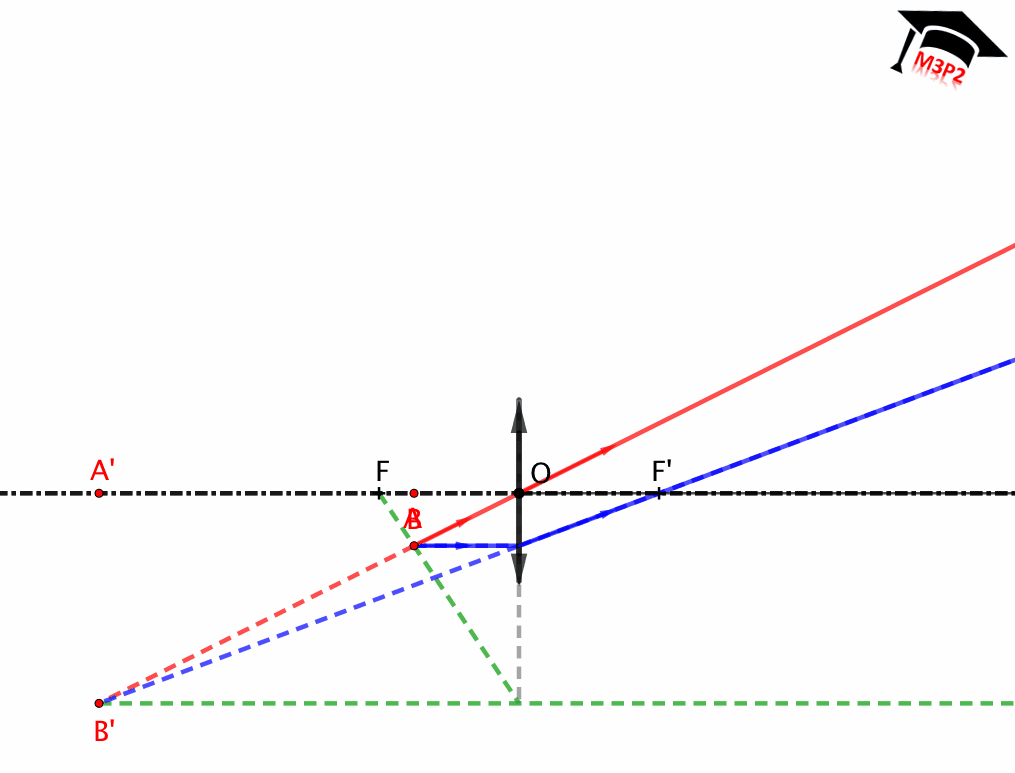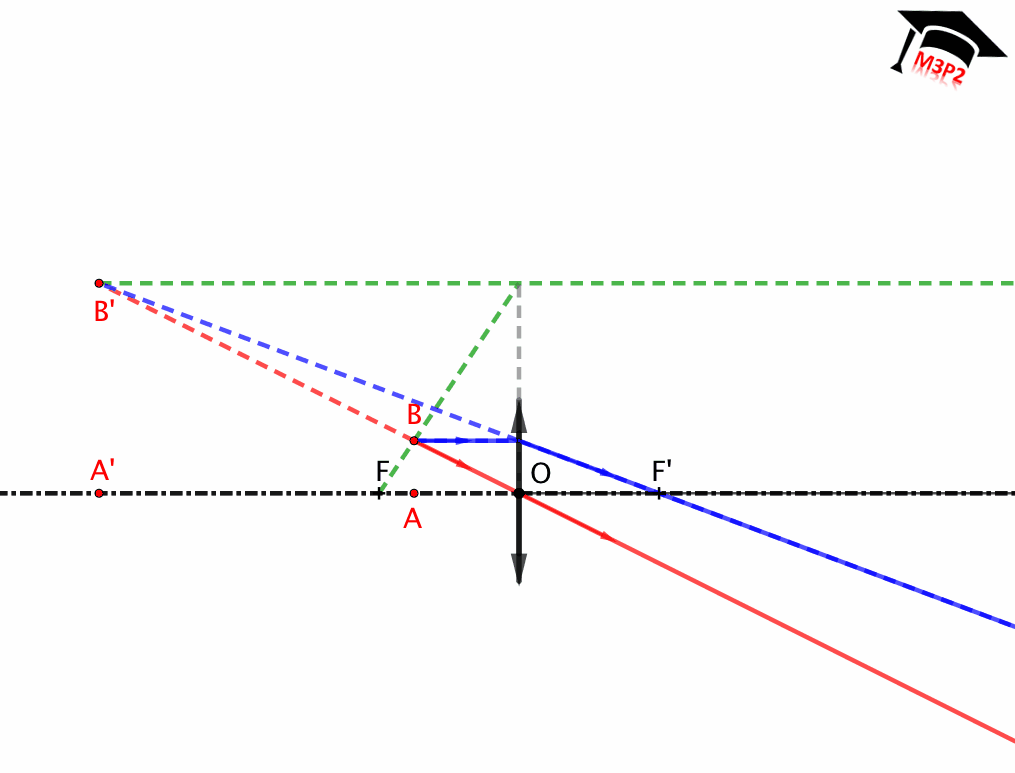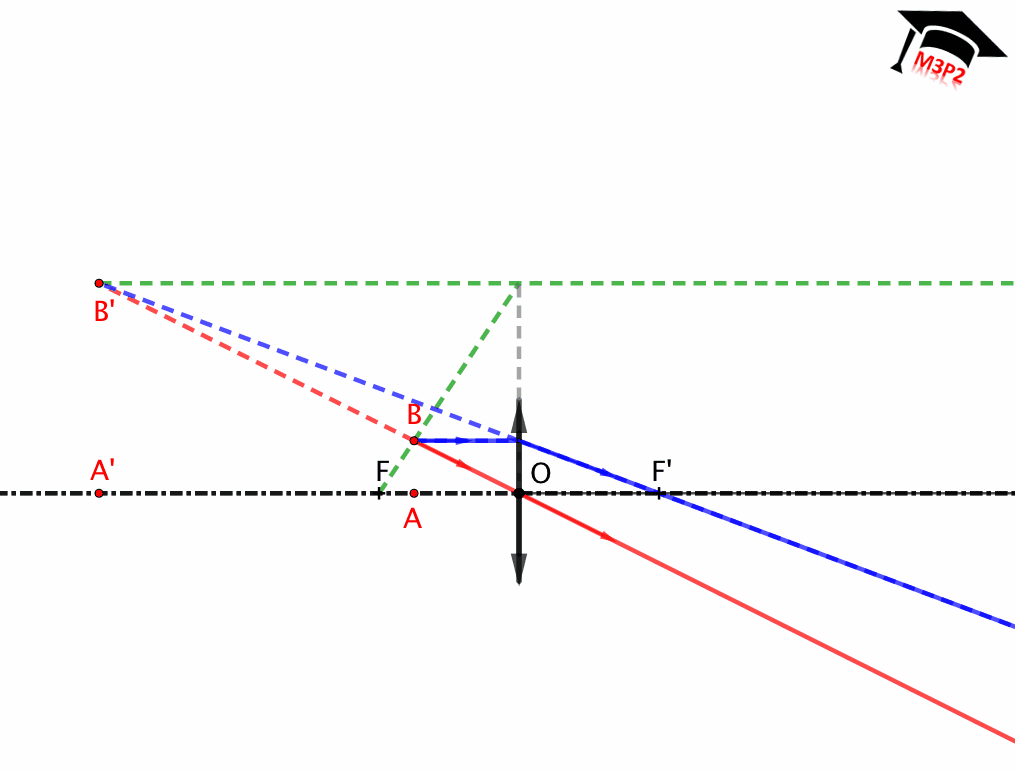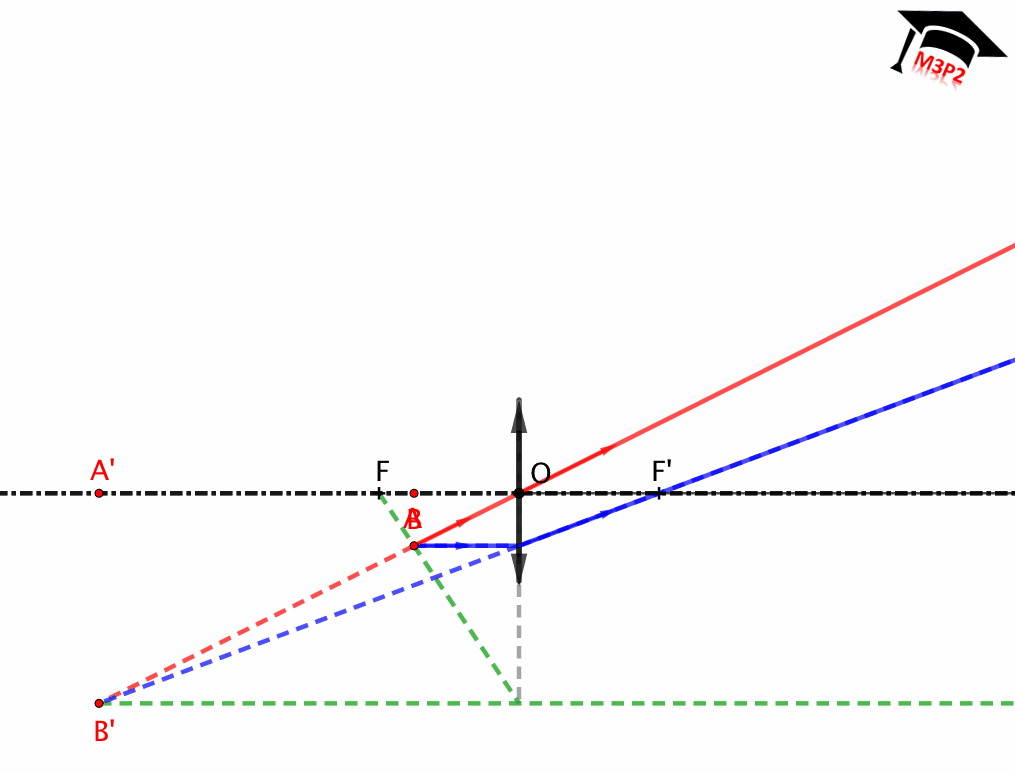
Lente delgada convergente
Para animaciones geogebra:
\ - Construcción gráfica
Haga clic aquí para ver la animación
\ - Construcción gráfica y haces de luz
Haga clic aquí para ver la animación
\ - Construcción gráfica y aumento transversal
Haga clic aquí para ver la animación
- Fuente puntual localizada entre ∞ y F
- Fuente puntual localizada entre F y O
- Punto objeto virtual (se explicará a nivel cerros).
Lente delgada divergente
(para construir)