courses/12.temporary_ins/15.electrokinetics/20.overview/cheatsheet.fr.md

title	published	routable	visible
Electrocinétique	false	false	false

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

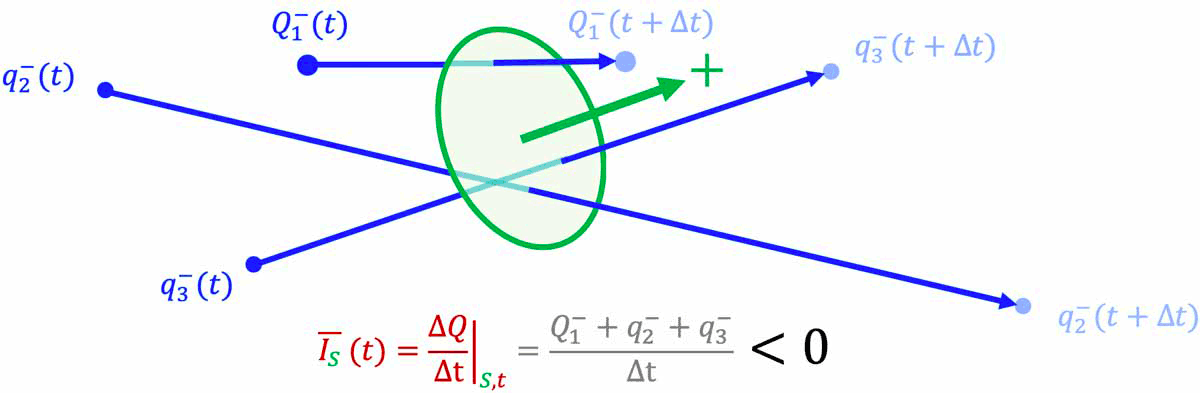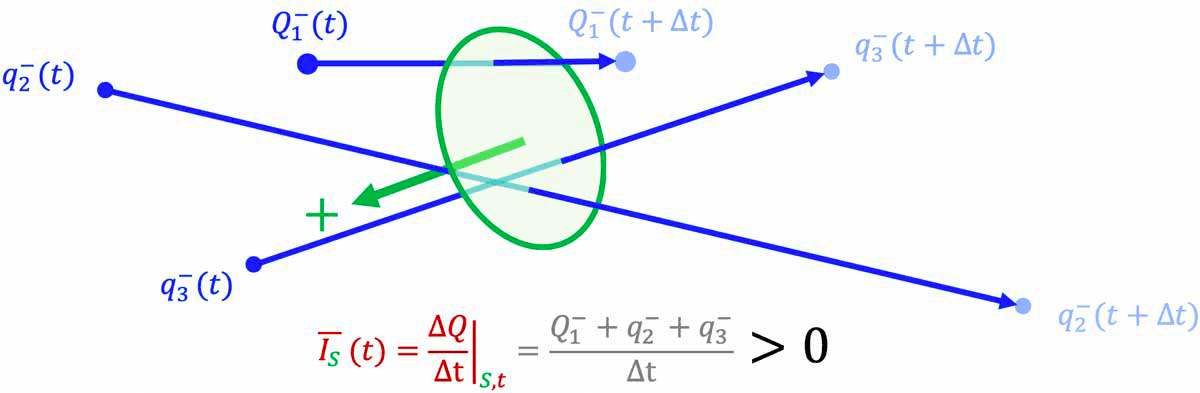
Vraiment pas au point. A revoir et réorganiser un minimum... Il manque aussi un signe moins dans l'équation de la figure current-intensity-definition-2_v1_L1200, lorsque I>0...

Qu'est-ce qu'un milieu conducteur électrique ?

Un milieu est électriquement conducteur si il contient des charges libres de se déplacer à travers le milieu sous l'influence d'un champ électrique aussi faible soit-il.

• Dans les conducteurs solides, les charges libres sont des électrons.
• Dans les conducteurs liquides (électrolytes), les charges libres sont des ions positifs et des ions négatifs.
• Dans les conducteurs gazeux (plasma), les porteurs de charges sont des électrons et des ions positifs.

Qu'est-ce qu'un courant électrique ?

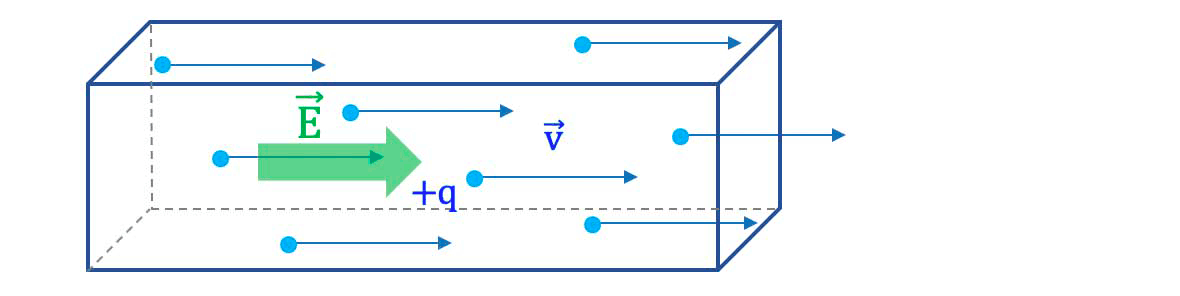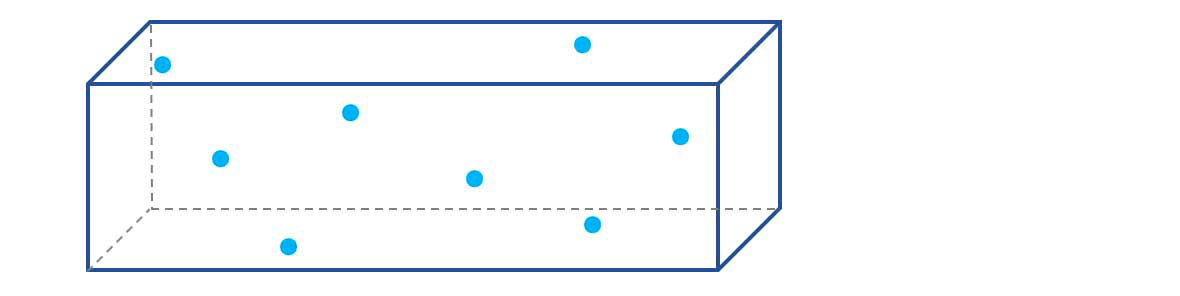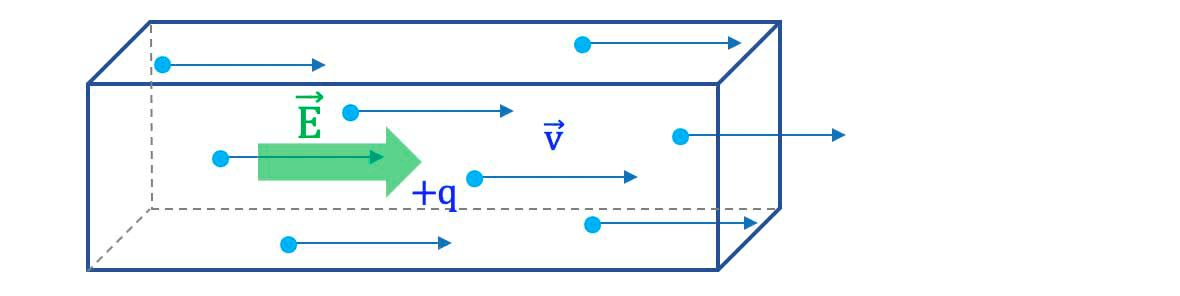
Un courant électrique est un mouvement d'ensemble de porteurs de charge électrique.

Qu'est-ce que l'intensité d'un courant électrique ?

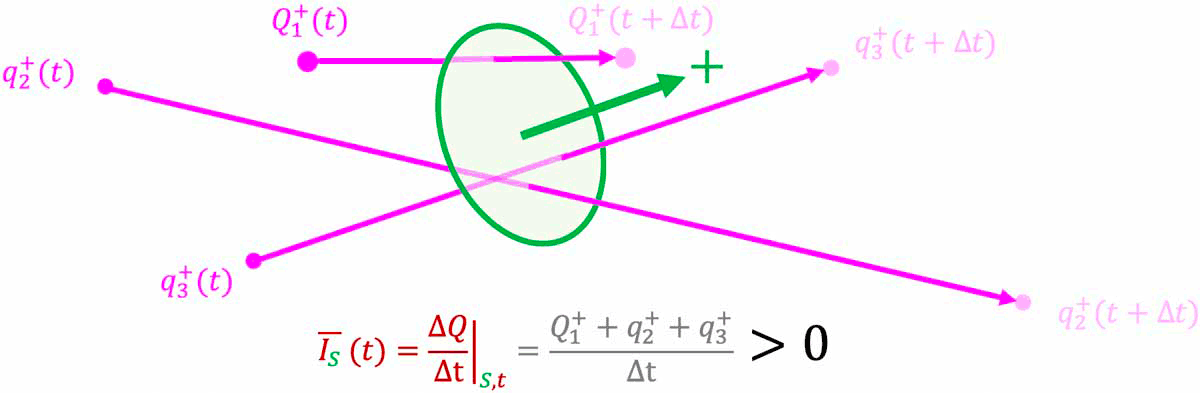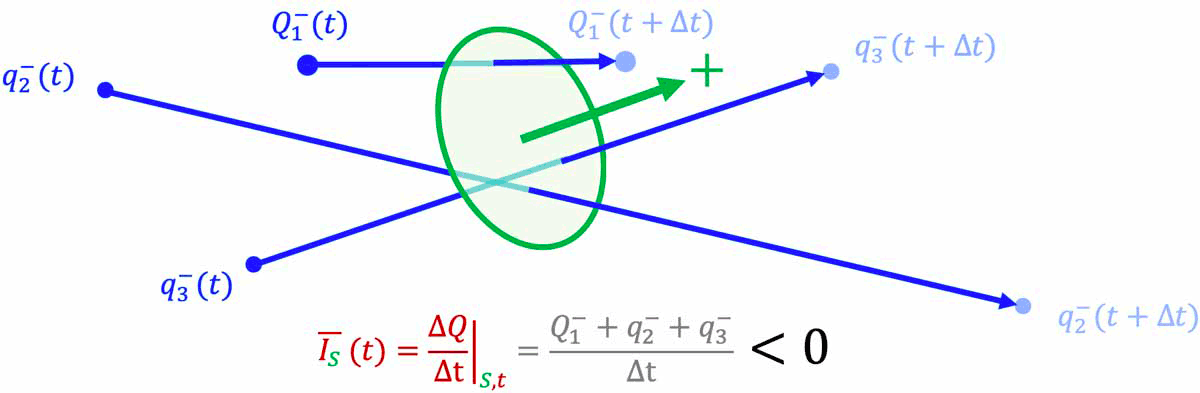
L'intensité $I$ du courant électrique à travers une surface orientée $S$ est égale à la charge électrique $\Delta Q$ qui traverse cette surface $S$ dans le sens positif de la surface pendant la durée $\Delta t$.

$I=\left. \dfrac{\Delta Q}{\Delta t} \right|_S$

L'intensité $I$ est ainsi une grandeur algébrique : elle peut être positive ou négative, et sa notation devrait être $\overline{I}$.

• Son signe dépend de l'orientation choisie de la surface $S$.

• Son signe dépend du signe de la charge qui traverse la surface orientée $S$.

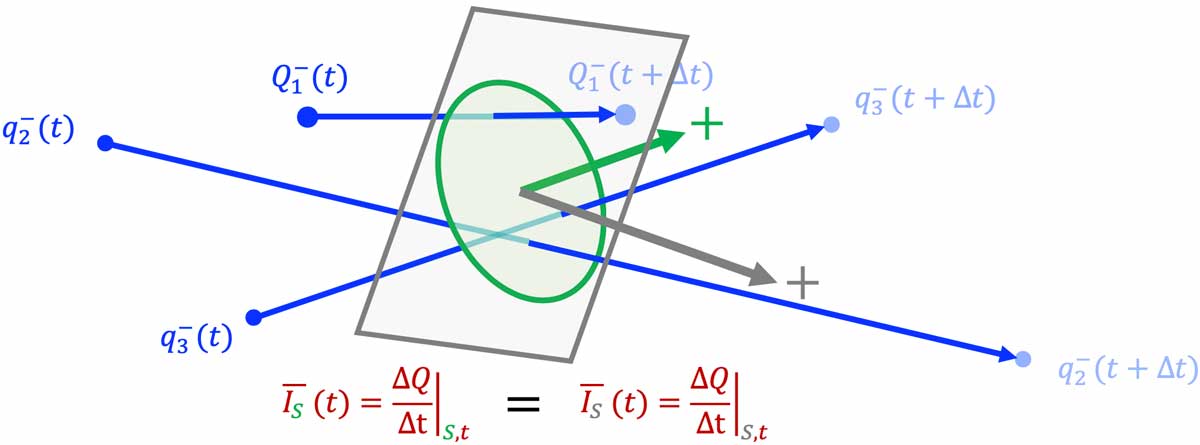
• Dans le cas générale, deux surfaces d'aires et d'orientation différentes peuvent être traversées par une même charge en un temps donné $\Longrightarrow$ les intensités mesurées sur la même plage de temps à travers ces deux surfaces peuvent être égales.

• L'Unité SI (SI : Système International d'unités) de l'intensité $I$ est l'Ampère, de symbole $A$.
  
  Un courant d'intensité d'un ampère ($1\,A$) correspond donc à une charge de 1 Coulomb ($1\,C$) qui traverse une surface donnée en une seconde ($1\,s$).

! Note : ! ! L'Ampère est une unité de base du système international d'unités, parmi les sept unités de base qu'il contient et qui sont le mètre, le kilogramme, la seconde, l'ampère, le kelvin, la mole et la candela. Toutes les autres unités, nommées unités dérivées, s'expriment en fonction des sept unités de base à partir d'une analyse dimensionnel.

!!!! Attention : !!!! !!!! Lorsque le sens de parcourt du courant électrique dans un circuit électrique est important dans plusieurs situations :
!!!! * lorsque le circuit comprend une diode. !!!! * lorsque l'on s'intéresse aux effets electromagnétiques induits par les courants. !!!! !!!! Le courant électrique étant la charge électrique qui traverse par unité de temps une surface donnée :
!!!! * Pour une surface fermée (ce qui signifie qu'elle délimite un volume, et qu'elle permet donc de définir un intérieur et un extérieur à ce volume) le sens du courant est le sens de déplacement d'une charge positive qui traverse par unité de temps la surface de l'intérieur vers l'extérieur (ou, équivalent, d'une charge nagétive qui traverse par unité de temps la surface de l'extérieur vers l'intérieur). !!!! !!!! * Pour une surface ouverte, les notions d'intérieur et d'extérieur ne peuvent être définie par la surface. Un sens positif de traversée de la surface doit alors être choisi arbitrairement. Le sens du courant est alors le sens de déplacement d'une charge positive qui traverse par unité de temps la surface dans son sens positif (ou, équivalent, d'une charge nagétive qui traverse par unité de temps la surface dans son sens négatif). !!!! !!!! !!!! !!!! Cette notion visuelle mais longue à expliquer en mots devient très simple et automatique lorsque le courant sera défini (et son intensité calculée) à partir du vecteur densité volumique de courant, et du vecteur représentatif d'une surface élémentaire.

Quelles différences entre des courants stationnaires, variables, alternatifs ?

• Un courant est dit stationnaire ou continu lorsque son intensité $I$ à travers une même surface ne dépend pas du temps.

• Un courant est dit variable, et se note $I(t)$* lorsque son intensité *$I$ change de valeur au cours du temps*.

• Un courant variable est dit alternatif lorsque le sens du mouvement d'ensemble des porteurs de charge s'inverse au cours du temps, donc lorsque son intensité en valeur algébrique change de signe au cours du temps.

Quelle différence entre intensité instantanée et intensité moyenne ?

• L'intensité instantanée est l'intensité du courant qui traverse la surface orientée S *sur une durée $\Delta t$, dans la limite où $\Delta t$ tend vers zéro :
  
  $I(t)=\lim_{\Delta t \rightarrow 0} \left.\dfrac{\Delta Q}{\Delta t} \right|_{S,t}= \left.\dfrac{dQ}{dt} \right|_{S,t}$

• L'intensité moyenne sur un intervale de temps $\Delta t$ est la valeur de l'intensité instantanée moyennée à chaque instant t *sur une durée $\Delta t$ :
  
  $<I(t)> = \dfrac{1}{\Delta t}\cdot \int_{t-\Delta t}^{t} I(t) \cdot dt$

Qu'est-ce que vitesse de dérive et mobilité dans les conducteurs solides ?

Vitesse de dérive dans un conducteur solide

• Dans un plasma peu dense, chaque particule libre de charge $q$ et de masse $m$ au repos est relativement libre de se déplacer. Sous l'effet de la force électrique $\overrightarrow{F_E}=q \cdot \overrightarrow{E}$, elle est accélérée $\overrightarrow{a}=\overrightarrow{F_E}/m$, et sa vitesse augmente constamment et peut atteindre des vitesses relativistes.

• Dans un matériau dense comme un conducteur solide, au cours de sa trajectoire chaque particule libre de charge $q$ subit pleins de "chocs" (expression classique) avec notamment les atomes du réseau matériel, qui relaxent sa quantité de mouvement et son énergie cinétique.
  
  $\Longrightarrow$ mouvement désordonné sans direction privilégiée, donc qui n'induit pas de courant électrique à travers une surface : c'est le mouvement d'agitation thermique.
  
  $\Longrightarrow$ à ce mouvement d'agitation thermique se superpose un lent mouvement de dérive en direction du champ électrique (matériaux isotropes) qui réaccélère la particule entre deux chocs : c'est un mouvement de dérive.

• Dans un volume mésoscopique de matériau conducteur et dans une description classique des forces moyennes qui agissent sur les particules libres chargées au sein de ce volume, les chocs agissent comme une force de frottement $\overrightarrow{F_{frot}}$ qui s'oppose à la force électrique $\overrightarrow{F_E}$.

• Lorsque ces deux forces sont égales en modules et de sens opposés $(\;\overrightarrow{F_{frot}}=-\overrightarrow{F_E}\;)$ , la force résultante s'annule, donc l'accélération moyenne s'annule et la population de particules chargées libres d'un même type se déplacent globalement d'un vecteur vitesse appelé vecteur vitesse de dérive $\overrightarrow{v_{d}}$.
  
  $\Longrightarrow$ de vitesse moyenne faible, mais de direction stable, le mouvement de dérive induit un courant électrique dans le matériau.

Mobilité d'un matériau conducteur

• Pour des valeurs de champ électrique pas "trop fort" (régime ohmique), la vitesse de dérive $\overrightarrow{v_d}$ est proportionnelle au champ électrique appliqué $\overrightarrow{E}$.

• Le rapport de proportionnalité entre $\overrightarrow{v_d}$ et $\overrightarrow{E}$ s'appelle la mobilité :
  
  $\overrightarrow{v_{d}}=-\mu \cdot \overrightarrow{E}$
  
  $\Longrightarrow$ Plus un matériau aura une mobilité importante pour ses électrons libres par exemple, plus la vitesse de dérive des électrons sera importante pour un même champ électrique appliqué, plus le courant électrique sera important pour une même densité volumique en électrons libres. Par ailleurs, plus le matériau répondra en fréquence.

Vecteur densité volumique de courant

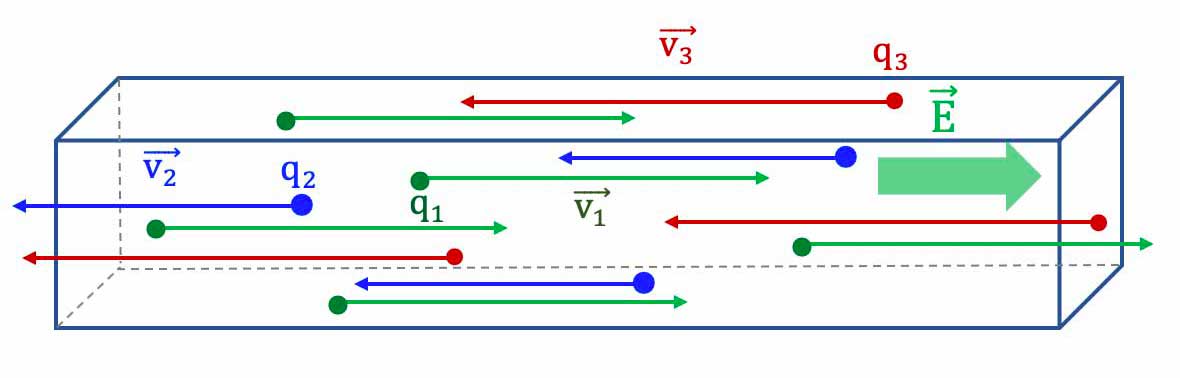
Avec un seul type de porteur de charge

Soit un matériau solide conducteur soumis à un champ électrique extérieur $\overrightarrow{E}$.

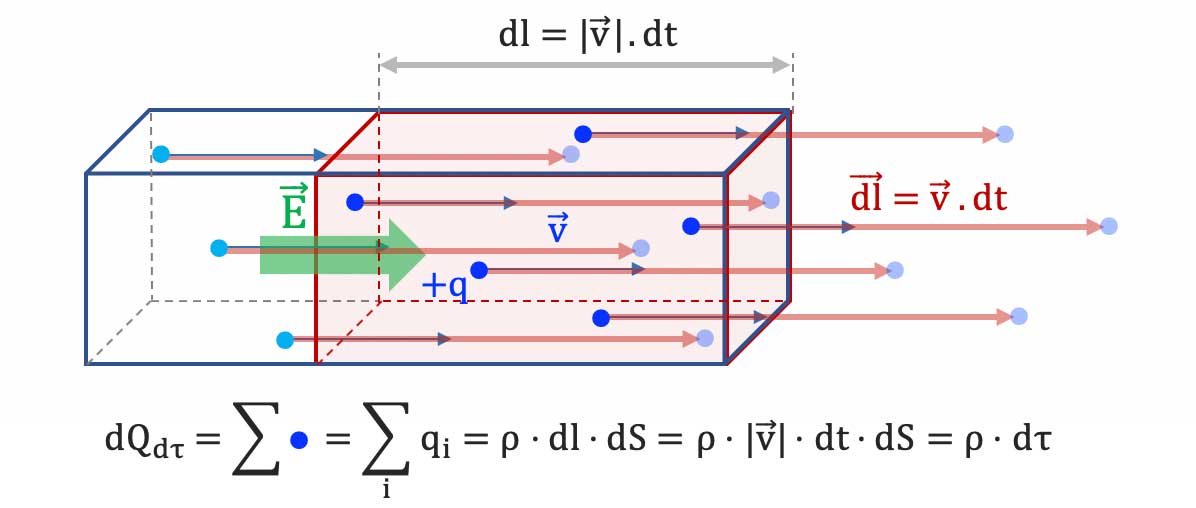
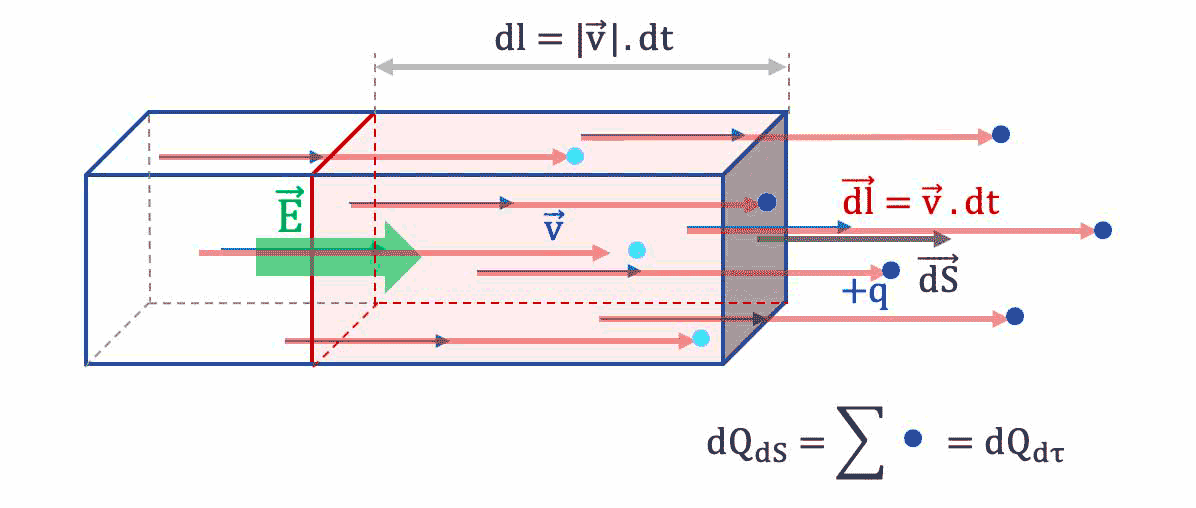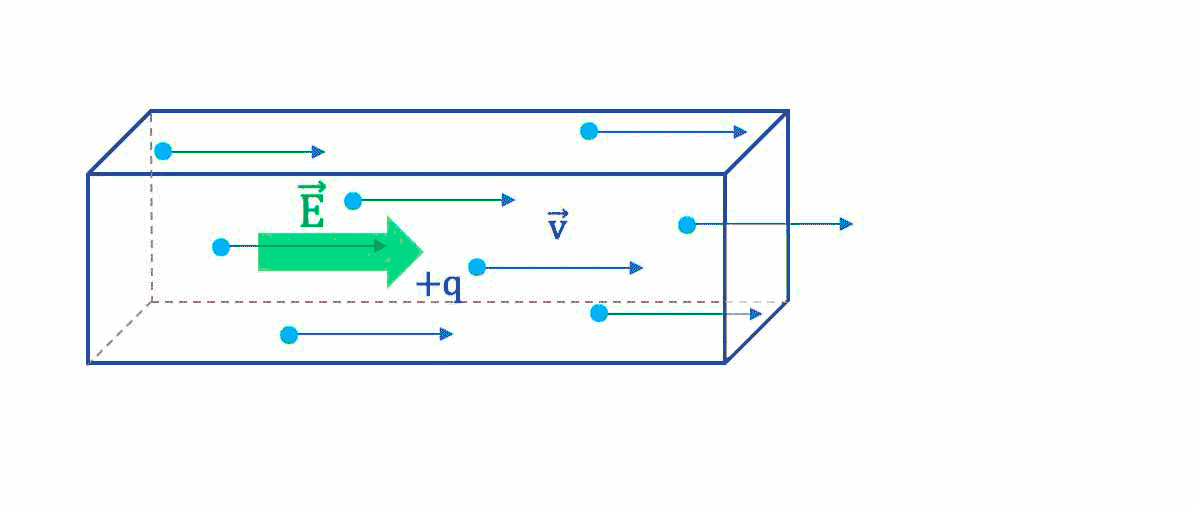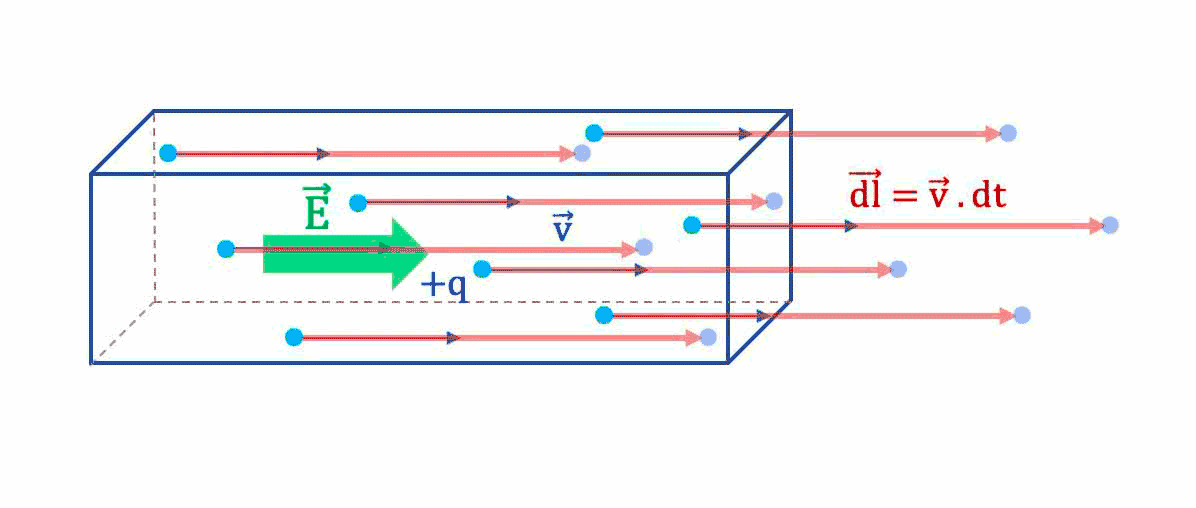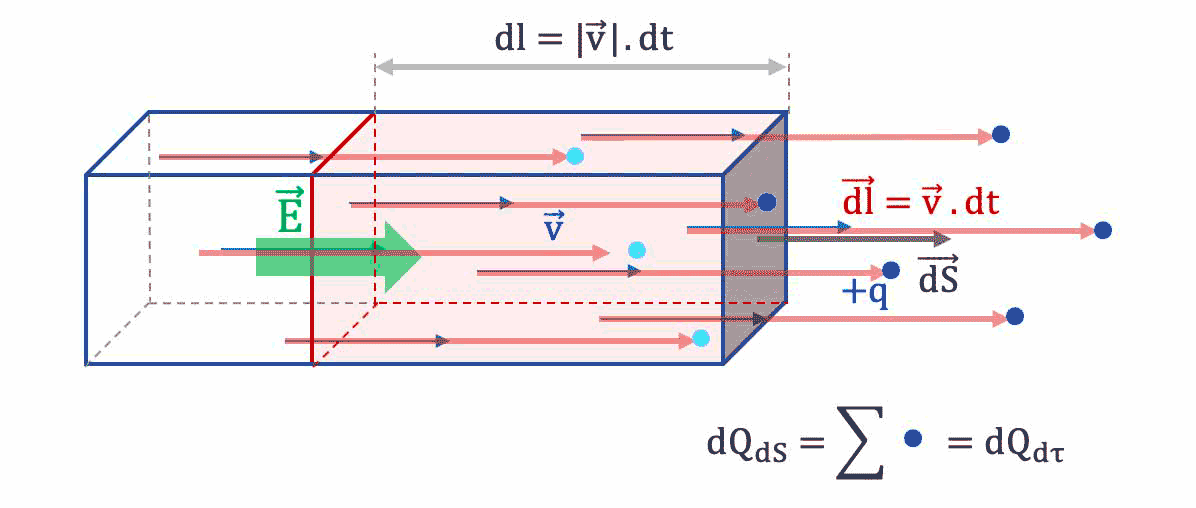
• En un temps $dt$, en moyenne un porteur de charge libre parcourt un vecteur distance $\overrightarrow{dl}$ telle que : $\overrightarrow{dl}= \overrightarrow{v_d} \cdot dt$

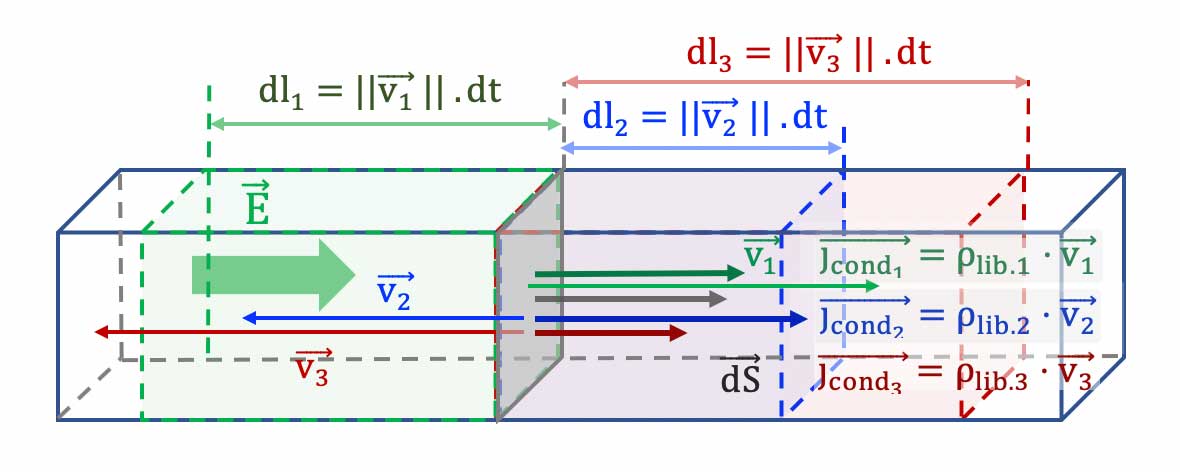
Soit une surface mésoscopique $\overrightarrow{dS}$ orientée en direction et sens de la vitesse de dérive $\overrightarrow{v_d}$ des porteurs de charge.

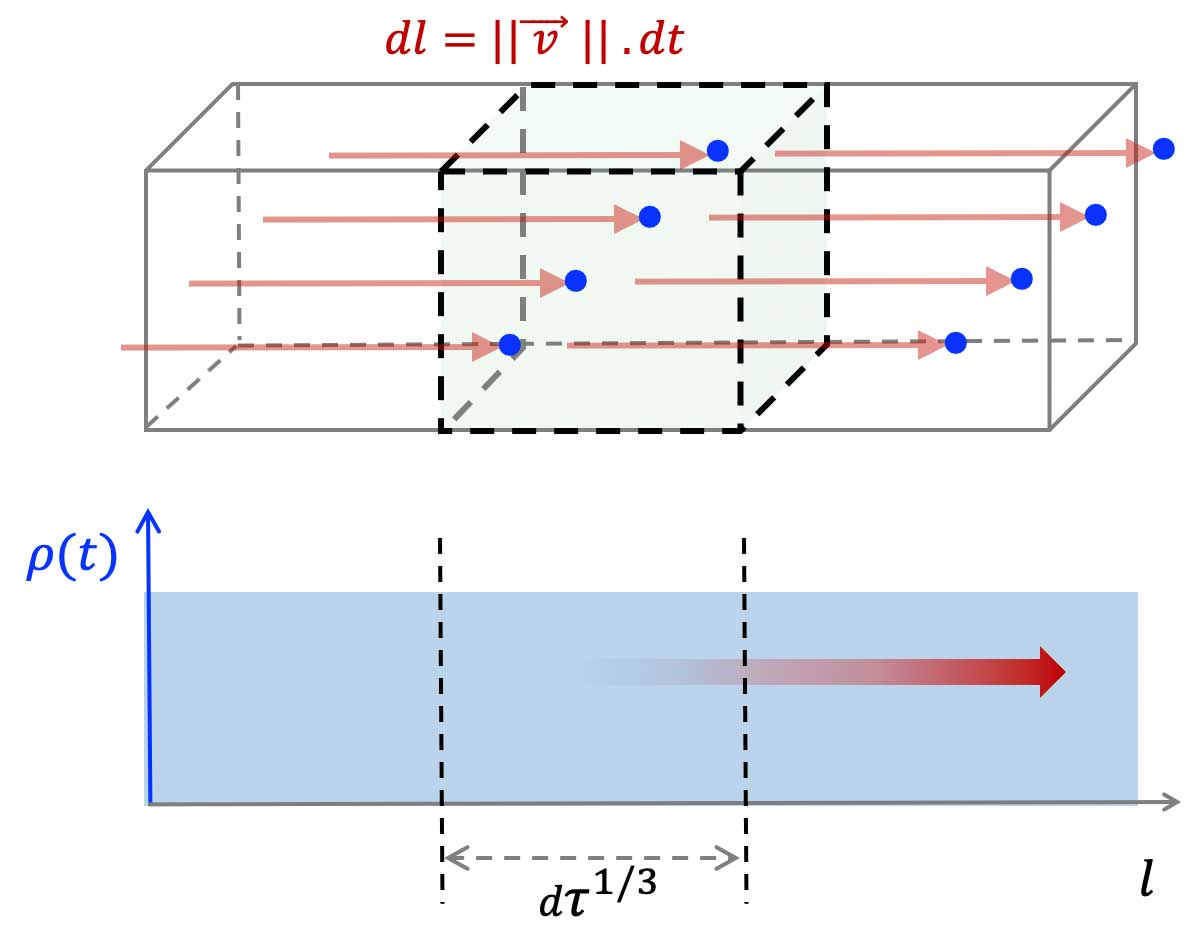
• Les porteurs qui traverseront en ce temps $dt$ la surface $\overrightarrow{dS}$ sont ceux situés dans le parallélépipède rectangle de section $dS$ et de longueur $d$, donc de volume mésoscopique $d\tau$ tel que :
  $d\tau = dl \cdot dS = ||\overrightarrow{v_d}|| \cdot dt\cdot dS$.
  
  La charge totale $dQ_{dS}$ qui traverse dans le temps $dt$ est donc la charge totale $dQ_{d\tau}$ des porteurs de charge libres contenus dans le volume $d\tau$.

• La charge totale $dQ_{dS}$ qui traverse $\overrightarrow{dS}$ dans le temps $dt$ est donc la charge totale $dQ_{d\tau}$ des porteurs de charge libres contenus dans le volume $d\tau$. Cette charge totale $dQ_{dS}=dQ_{d\tau}\;(C)$ est donc le produit de la densité volumique de charges libres $\rho \;(C\,m^{-3})$ dans le matériau multipliée par le volume $d\tau \; (m^{-3})$ :

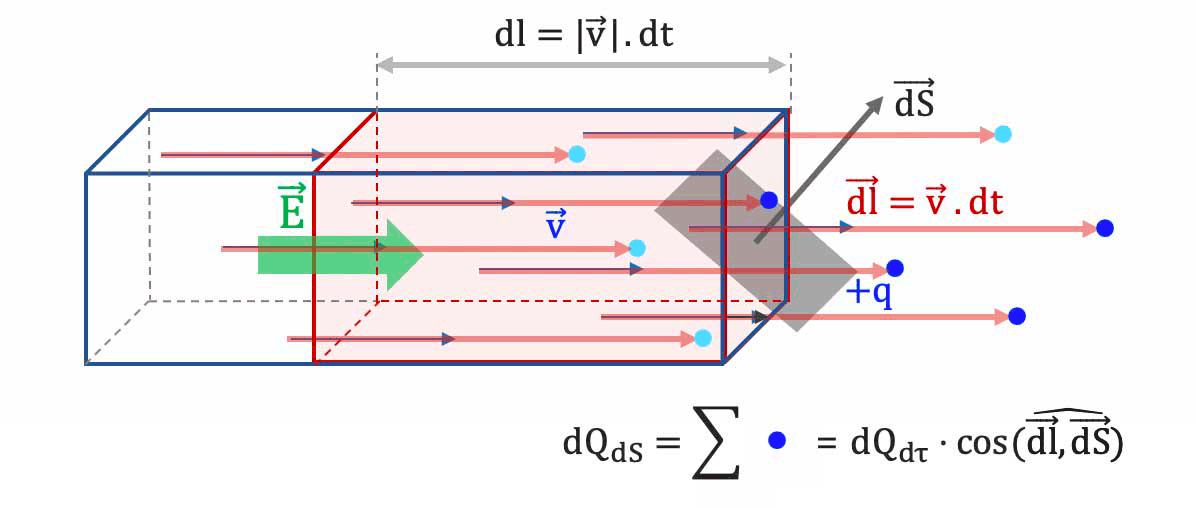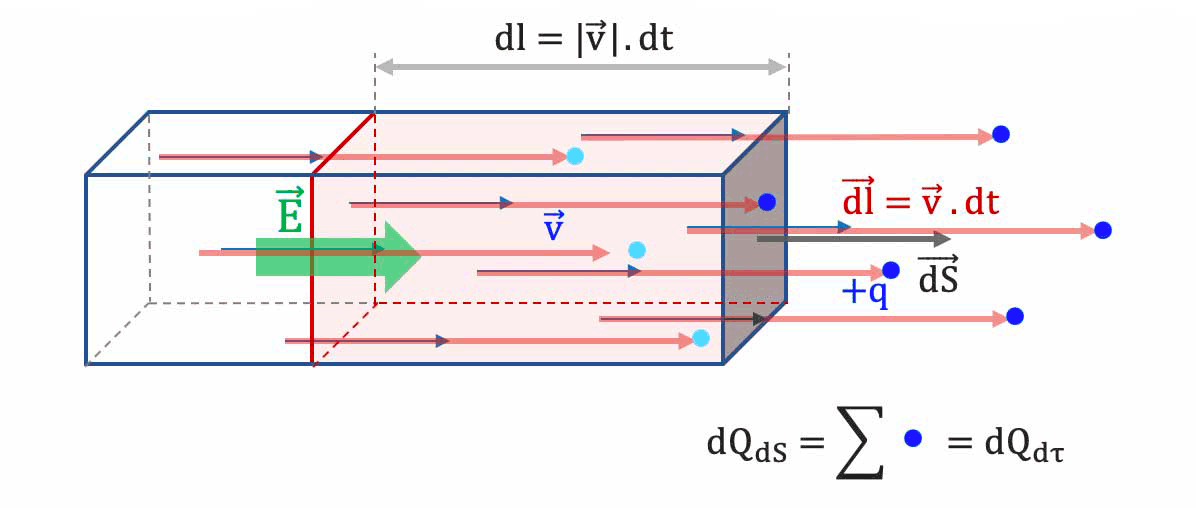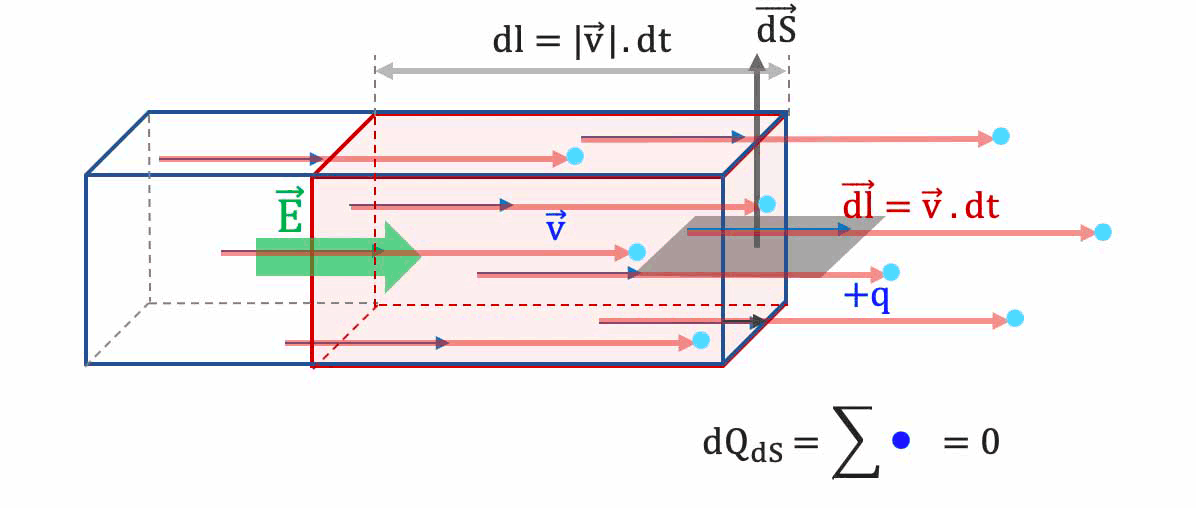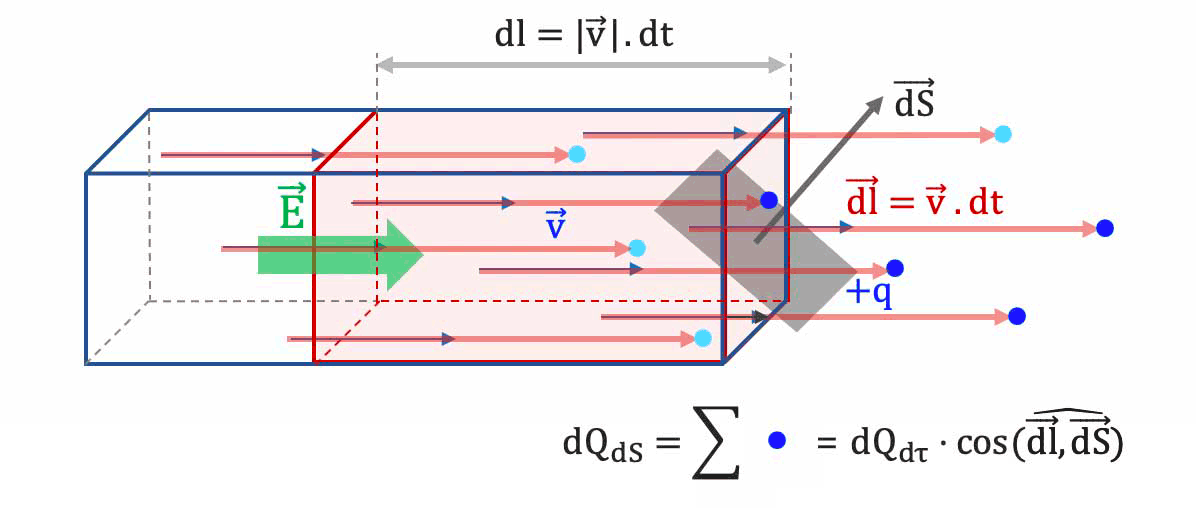
La surface mésoscopique $\overrightarrow{dS}$ n'est pas orientée en direction et sens de la vitesse de dérive $\overrightarrow{v_d}$ des porteurs de charge.

• $\longrightarrow$ seule une partie des charges contenues dans le volume $d\tau=|\overrightarrow{v}|.dt.dS$ franchissent cette surface.
  
  La fraction des charges dans la volume $d\tau$ qui traversent la surface est $cos(\widehat{\vec{v},vec{dS}})$.

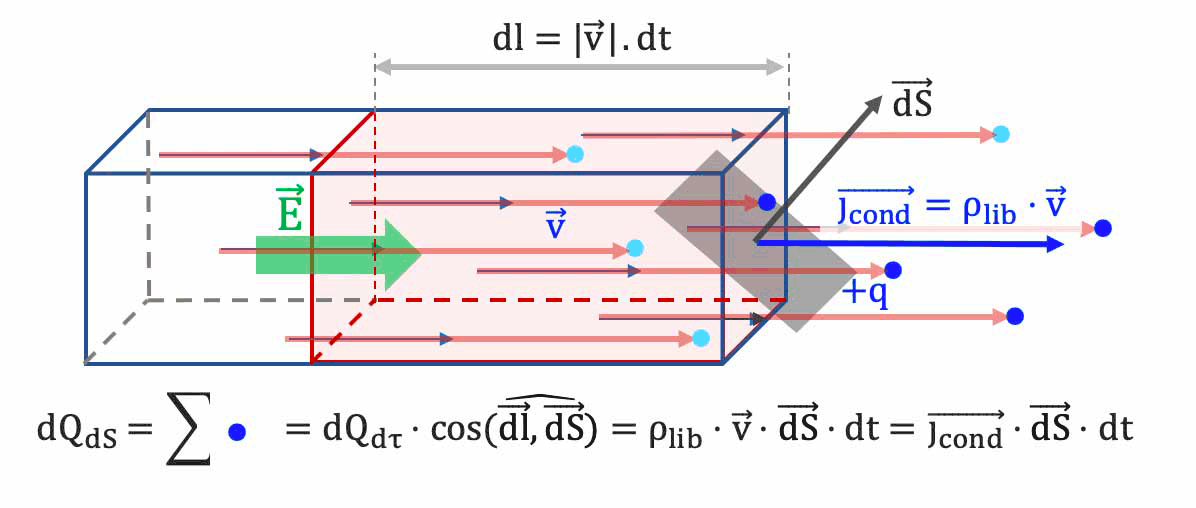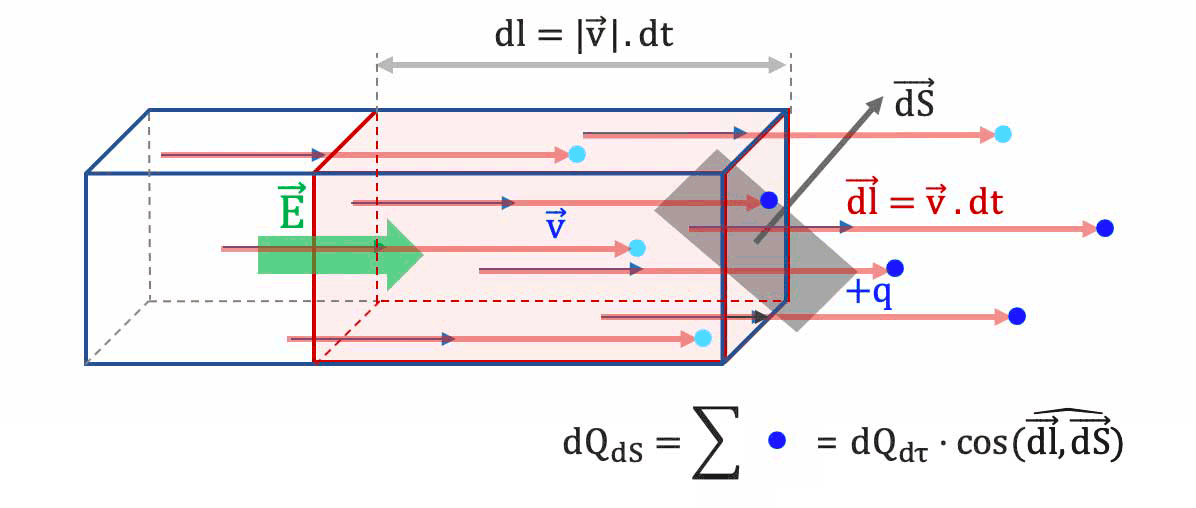
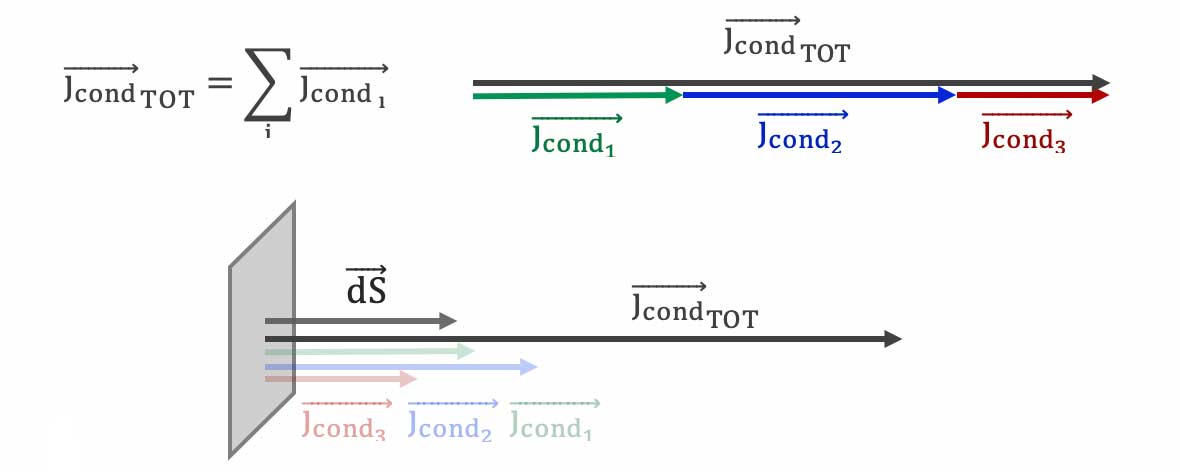
• Nous appelons vecteur densité volumique de courant (de conduction) $\overrightarrow{j_{cond}}$ ** le produit de la densité volumique de charges libres $\rho_{lib}$ par le vecteur vitesse de dérive $\overrightarrow{v_{d}}$ des porteurs libres de ces charges :
  
  $\overrightarrow{j_{cond}} = \rho_{lib} \cdot \overrightarrow{v_d}$**

• Équation aux dimensions et unité SI du vecteur densité volumique de courant :
  
  $[j_{cond}] = [rho_{lib}] \cdot [{v_d}]= [Q] \cdot L^{-3} \cdot L \cdot T^{-1}= [Q] \cdot T^{-1} \cdot L^{-2}= I \cdot L^{-2}$
  
  Unité SI : **ampère par mètre carré : $Am^{-2}$`.

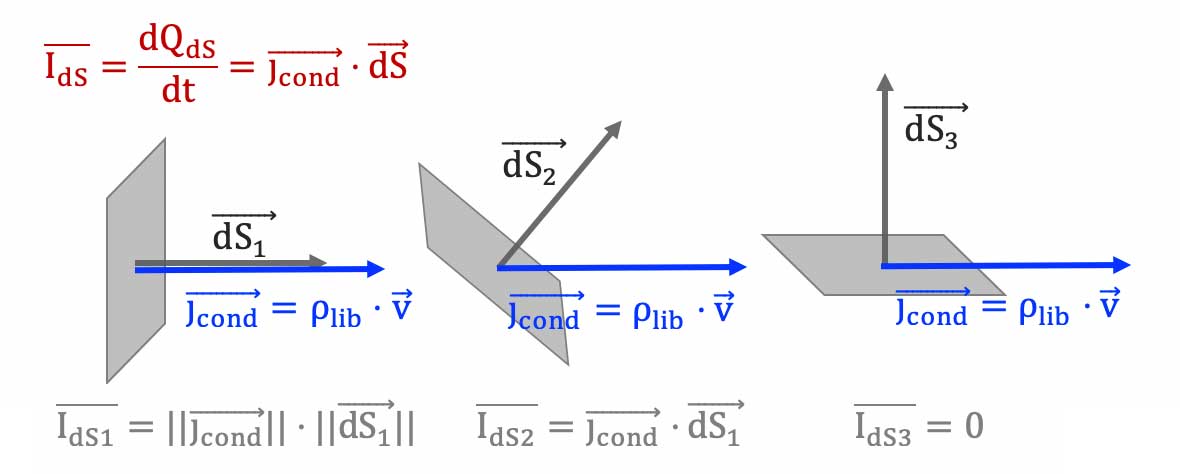
• L'intensité $dI$ qui traverse en un temps $dt$ cette surface $dS$ d'orientation quelconque donnée par le vecteur $\overrightarrow{dS}$ s'exprime donc :
  
  $dI = \dfrac{dQ_{dS}}{dt}= \dfrac{dQ_{d\tau}}{dt}= \rho_{lib} \cdot \overrightarrow{v_d} \cdot dt \cdot \overrightarrow{dS}\;\;\;\;\Longrightarrow$ $dI = \overrightarrow{j_{cond}} \cdot \overrightarrow{dS}$

Que représente le vecteur densité superficielle de courant ?

Quelle équation indique la conservation de la charge ?

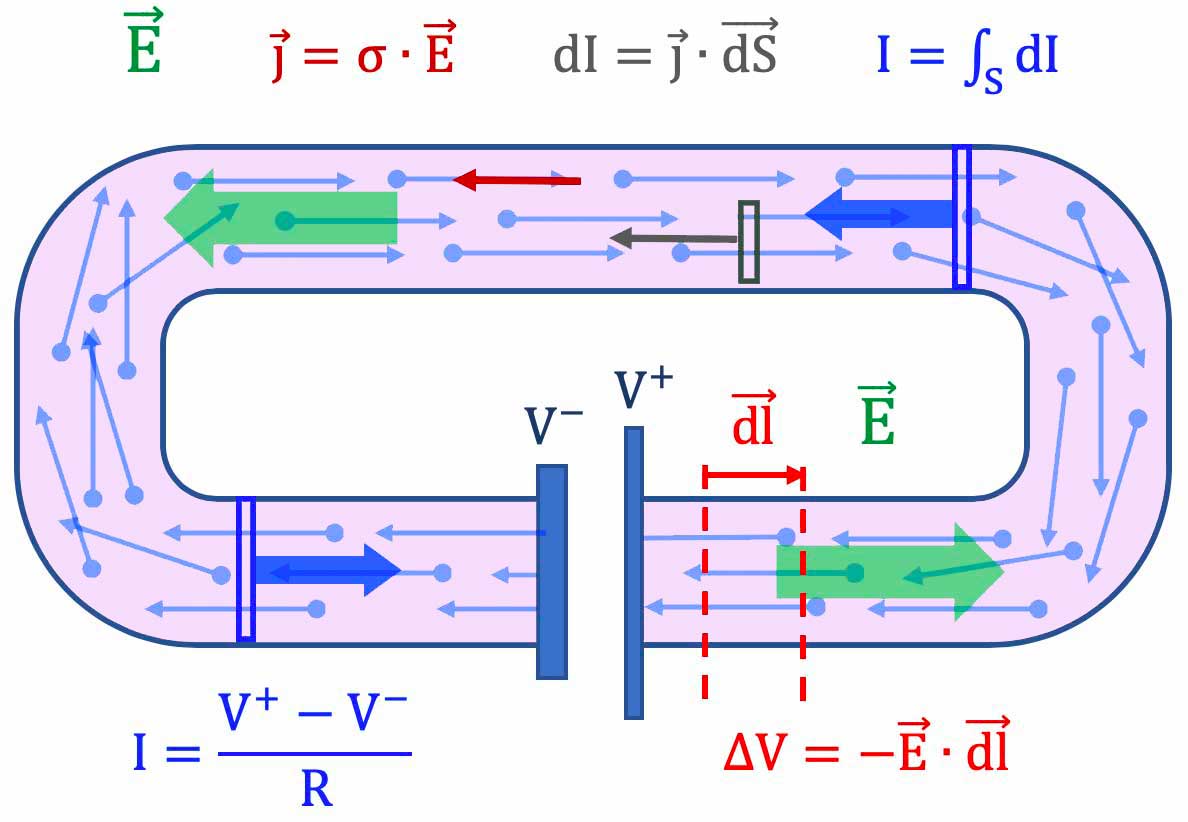
Quelle est la loi d'Ohm ?

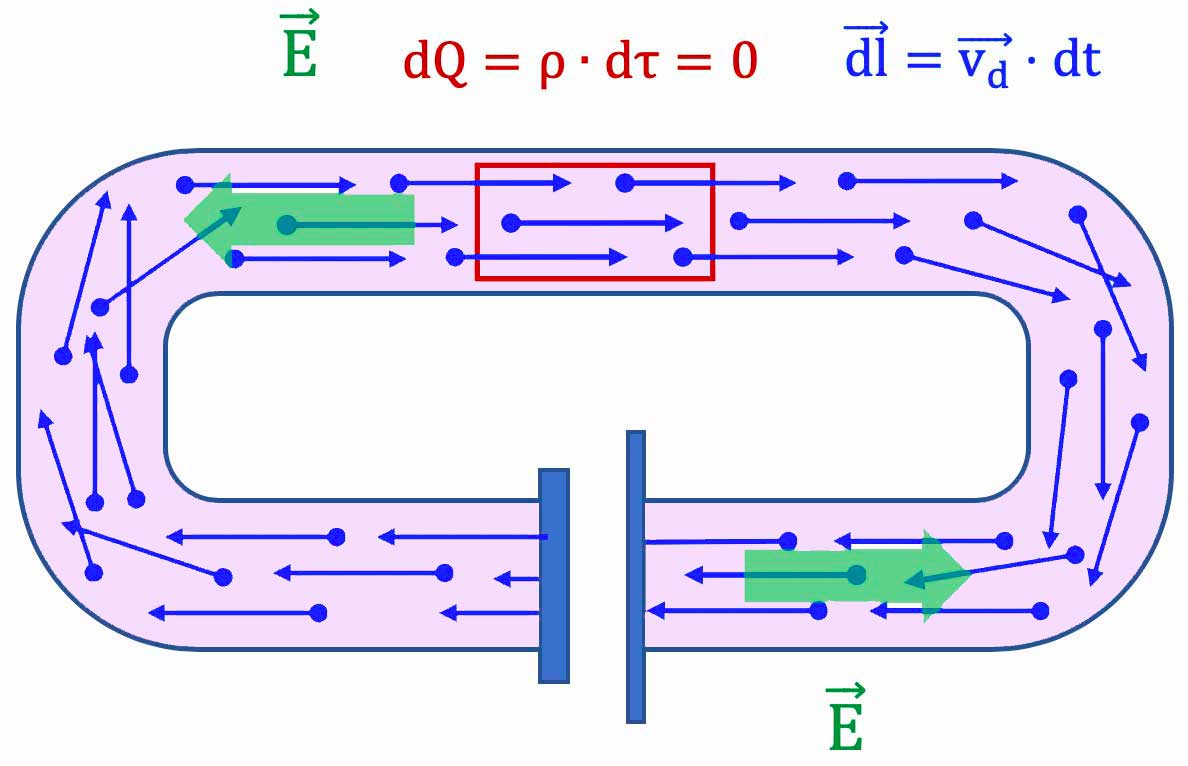
Un circuit conducteur est-il chargé ?

Probablement circuit conducteur en régime stationnaire ou lentement variable