9.1 KiB
| title | published | routable | visible | lessons |
|---|---|---|---|---|
| Magnétostatique 2 | true | true | false | {slug stationary-magnetic-field} {order 3} |
!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.
Quels sont les effets d'un champ magnétique stationnaire ?
Quelle force sur une particule chargée en mouvement ?
Les effets d'un champ magnétiques sont induits par le champ d'induction magnétique $\overrightarrow{B}$.
Ce champ $\overrightarrow{B}$ exerce une force magnétique $\mathbf{\overrightarrow{F_{mag}}}$ sur toute particule chargée de charge $q$ et mobile dans le référentiel d'étude, c'est à dire animée d'une vitesse $\overrightarrow{v}$ non nulle.
L'expression de la force magnétique est $\overrightarrow{F_{mag}}$ :
$\mathbf{\overrightarrow{F}_{mag} = q ; (\overrightarrow{v}\land\overrightarrow{B})}$
Quelle force sur un conducteur parcouru par un courant ?
Le contexte
- Soit un circuit conducteur $
C$ parcouru par un courant électrique $I$ et plongé dans un champ magnétique $\overrightarrow{B}$. - Soit un élément $
dC$ de $C$, de longueur $dl$ et de section $dS$ , de volume $d\tau=dl\cdot dS$ - Soit $
\rho_{liée}$ la densité volumique de charges liées (les ions positifs du métal conducteur) dans cet élément $dC$. - Soit $
\rho_{libre}$ la densité volumique de charges libres (les électrons libres du métal conducteur). - Soit $
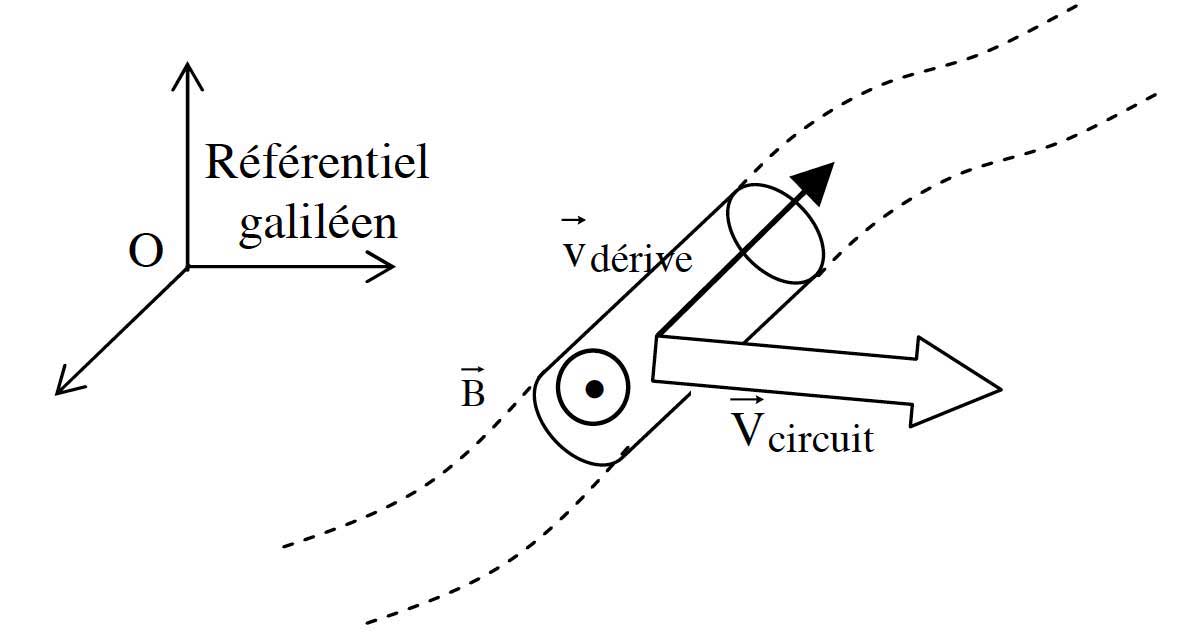
\overrightarrow{v}_{dér\,/\,dC}$ la vitesse de dérive (vitesse orientée sous l'action d'un champ électrique) des charges libres par rapport aux charges fixes (donc par rapport à un référentiel lié à l'élément de circuit $dC$). - Soit $
\overrightarrow{V}_{dC\,/\,\mathcal{R}}$ la vitesse de l'élément de circuit $C$ dans le référentiel du laboratoire supposé galiléen.
- Le courant $
I$ parcourant le circuit $dC$ (donc traversant la section droite $dS$ du circuit) est :
$I= \overrightarrow{j}\cdot\overrightarrow{d_S} = \rho_{libre}\cdot\overrightarrow{v}_{dér\,/\,dC}\cdot \overrightarrow{d_S}$ - Ce circuit est plongé dans un champ d'induction magnétique $
\overrightarrow{B}$ uniforme.
La force de Laplace
-
L'expression de la force magnétique $
\overrightarrow{dF_B}$ s'exerçant sur cet élément de circuit $dC$ est :
$\overrightarrow{dF_B}= \rho_{liée}\cdot d\tau\cdot(\overrightarrow{V}_{dC\,/\,\mathcal{R}}\wedge\overrightarrow{B})\;$$\quad +\; \rho_{libre}\cdot d\tau\cdot [(\overrightarrow{v}_{dér\,/\,dC} +\overrightarrow{V}_{dC\,/\,\mathcal{R}})\wedge\overrightarrow{B}]$
$\overrightarrow{dF_B}= (\rho_{libre}+\rho_{liée}) \cdot d\tau \cdot (\overrightarrow{V}_{dC\,/\,\mathcal{R}} \wedge \overrightarrow{B})$$\quad + \rho_{libre} \cdot d\tau \cdot (\overrightarrow{v}_{dér\,/\,dC} \wedge \overrightarrow{B})$ -
Le matériau conducteur du circuit est neutre : en absence de courant il y a autant de protons positifs que d'électrons liés et libres dans tout volume mésoscopique $
d\tau$ du conducteur :
$\rho=\rho_{liée} + \rho_{libre}=0$
Lorsque le circuit est traversé par un courant stationnaire, cette neutrailté est conservée dans tout $d\tau$ : en effet au cours d'un temps $dt$ une même charge $dq$ (due aux électrons libres) à la fois quitte et entre dans tout volume $d\tau$, maintenant sa neutralité, ce qui entraîne :
$\dfrac{\partial \rho}{dt}=\dfrac{\partial \,(\rho_{liée} + \rho_{libre}}{dt}=0$$\quad\Longrightarrow \overrightarrow{dF_B}= \rho_{libre} \cdot d\tau \cdot (\overrightarrow{v}_{dér\,/\,dC} \wedge \overrightarrow{B})$. -
On nomme force de Laplace cette force magnétique $
\overrightarrow{dF_B}$ qui s'exerce sur chaque élément $dC$ du circuit :
$\mathbf{\overrightarrow{dF}_{Laplace}= \rho_{libre} \cdot d\tau \cdot (\overrightarrow{v}_{dér\,/\,dC} \wedge \overrightarrow{B})}$ -
Cette force de Laplace sur chaque élément $
dC$ peut induire :
- une déformation du circuit électrique dans le cas d'un circuit déformable.
- une force de Laplace $\overrightarrow{F}_{Laplace}=\oint_C \overrightarrow{dF}_{Laplace}$ qui s'aplique à l'ensemble du circuit dans le cas d'un circuit rigide.
Dans ces deux cas, la force de Laplace peut modifier le mouvement du circuit électrique.