11 KiB
| title | published | routable | visible | lessons |
|---|---|---|---|---|
| Magnétostatique 1 | true | true | false | {slug stationary-magnetic-field} {order 2} |
!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.
Quelles sont les causes d'un champ magnétique stationnaire ?
- Les causes d'un champ magnétique sont des courants électriques, donc toute particule chargée en mouvement.
Comment créer un champ magnétique stationnaire ?
- Technologiquement, dans le vide ou en absence de matériaux magnétiques, un champ magnétique stationnaire est créé par des courants constants dans des circuits conducteurs immobiles.
- Tout courant électrique, microscopique comme macroscopique, par la pensée peut être décomposé en ses éléménts de courant.
!!! Exemple de courants :
!!! * microscopiques : un flux d'électrons extraits d'une cathode chauffée et accélérés par une anode se propageant dans le vide.
!!! * macroscopiques : les courants de conduction circulant dans un circuit conducteur soumis à une différence de potentiel électrique.
Qu'est-ce qu'un élément de courant ?
-
Élément de courant = courant infinitésimal = courant élémentaire.
terminologie recommandée -
Un courant élémentaire $
\mathbf{I \cdot\overrightarrow{dl}}$ en un point P de l'espace peut aussi s'exprimer :
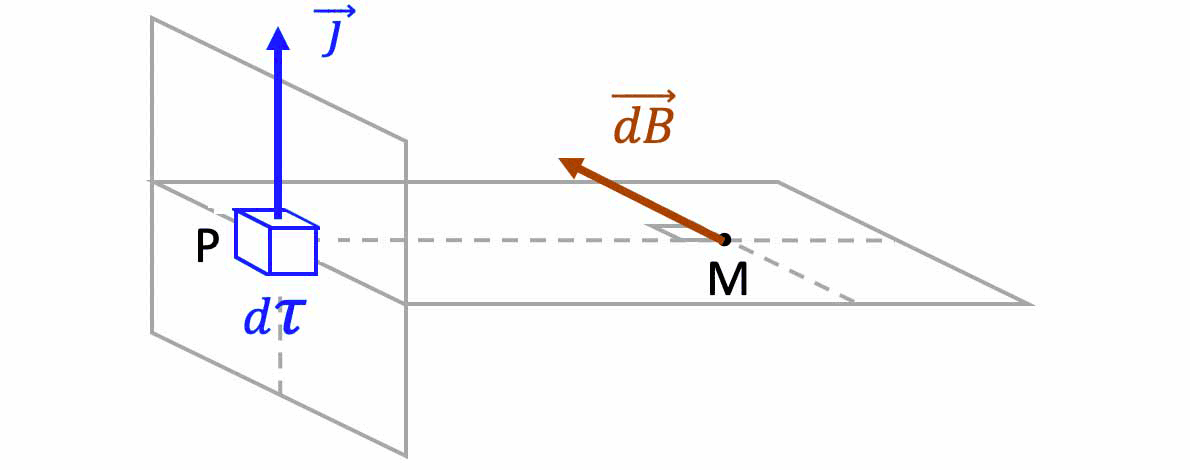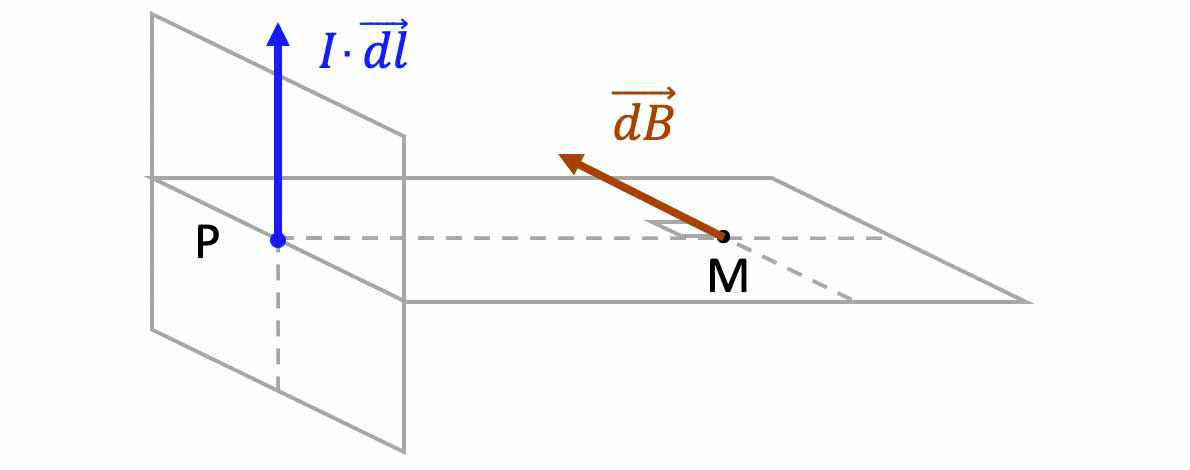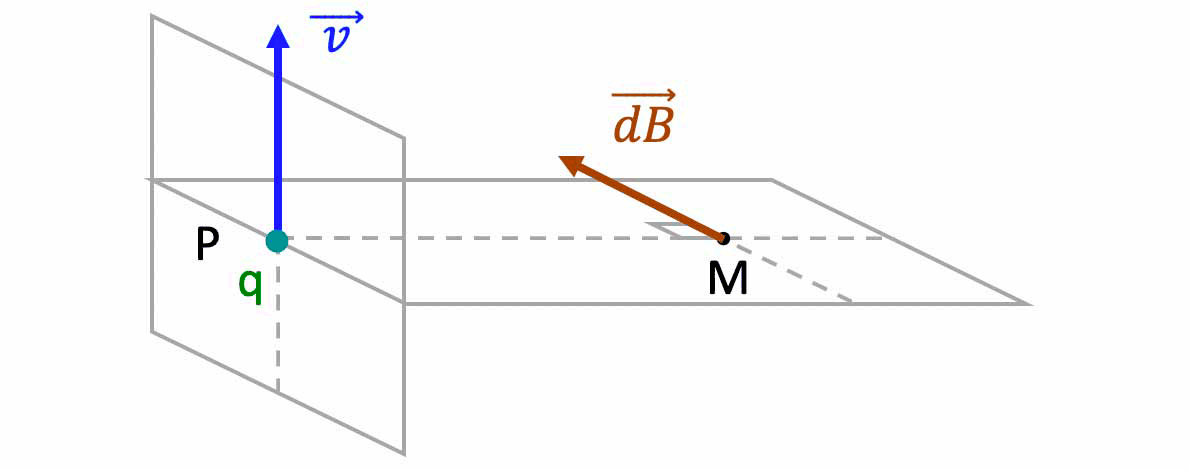
- en fonction du vecteur densité volumique $\overrightarrow{j}$ sur un volume élémentaire $d\tau$ au point P.
- en terme de charge élémentaire $q$ se déplaçant à la vitesse $\overrightarrow{v}$, de sorte que nous avons l'équivalence :
$\mathbf{I \cdot\overrightarrow{dl} \quad\equiv ;\overrightarrow{j} \cdot d\tau\quad \equiv ;q \cdot \overrightarrow{v}}`$ -
Les équations aux dimensions de ces expressions équivalentes montrent qu'elles sont caractérisées par la même grandeur physique, un courant électrique multiplié par une longueur :
- $[I \cdot L]= I \cdot L$
- $[q \cdot v]=[q]\cdot[v] = [q]\cdot L \cdot T^{-1}$$\quad = ([q]\cdot T^{-1})\cdot L = I \cdot L$
- $[j \cdot \tau]=[j]\cdot L^3 = I \cdot L^{-2} \cdot L^3 = I \cdot L$ -
Quelque soit l'expression utilisée, l'unité d'un élément de courant est l'Ampère mètre, $
\mathbf{A\cdot m}$ , dans le système internationale de mesure (SI).
Champ magnétique créé par un courant élémentaire : loi de Biot et Savard
-
Permet le calcul direct du champ magnétique créé en tout point de l'espace par des courants.
-
Les effets induits du champ magnétique ( force magnétique, force de Laplace, moments et couple sur une spire de courant, champ électromoteur et force électromotrice ) sont fonction du vecteur induction magnétique $
\overrightarrow{B}$. Le champ d'induction magnétique $\overrightarrow{B}$ est donc le champ fondamental à prendre en compte pour décrire les effets magnétiques. -
La loi de Biot et Savart exprimée en fonction du champ d'induction magnétique $
\overrightarrow{B}$ ) donne l'expression du champ magnétique élémentaire $d\overrightarrow{B}_M$ créé dans le vide, en tout point $M$ de l'espace par un élément de courant $I \cdot\overrightarrow{dl}_P$ localisé en un point $P$, s'écrit :
$\mathbf{\overrightarrow{dB}_M=\dfrac{\mu_0}{4\pi}\cdot\dfrac{I\cdot\vec{dl}_P\land\overrightarrow{PM}}{||\,\overrightarrow{PM}\,||^{\,3}}}$
soit encore :
$\mathbf{\overrightarrow{dB}=\dfrac{\mu_0}{4\pi}\cdot\dfrac{I\cdot\overrightarrow{dl}\land\overrightarrow{r}}{r^3}=\dfrac{\mu_0}{4\pi}\cdot\dfrac{I\cdot\overrightarrow{dl}\land\overrightarrow{e_r}}{r^2}}$, avec $\overrightarrow{r}=r\;\overrightarrow{e_r}$ et $r>0$, l'élément de courant étant localisé en $\overrightarrow{r}=\overrightarrow{0}$,
où $\mu_0$ est la constante magnétique, encore appelée perméabilité magnétique du vide. Son unité et sa valeur dans le système international sont :
$\mu_0 = 1.256\,6... \cdot 10^{-6}\; kg\,m\,A^{-2}\,s^{-2}$$\quad\approx 4\pi \cdot 10^{-7} \;T\,m \,A^{-1}$ -
*Unité SI de champ d'induction magnétique $
\overrightarrow{B}$ * : Le tesla (T).
!! Pour aller plus loin : sur la nature de $\overrightarrow{B}$ :
!! Dans la définition de $\overrightarrow{B}$ entre un produit vectoriel de deux vecteurs vrais (deux vecteurs polaires), donc dans sa définition entre une fois la règle d'orientation de l'espace $\Longrightarrow$ l'induction magnétique $\overrightarrow{B}$ est un pseudo-vecteur (ou vecteur axial).
!!
!! Cette remarque est importante pour ceux qui devront maîtriser les équations de l'électromagnétisme (les équations de Maxwell). Vecteurs vrais (ou vecteur polaires) et pseudo-vecteurs (ou vecteurs axiaux) se comportent différemment lors de certaines opérations de symétrie. Leur distinction sera fondamentale dans la compréhension et l'utilisation des théorèmes de Gauss en électrostatique et d'Ampère en magnétostatique, première étape avant d'aborder l'électromagnétisme de Maxwell.
!!
!! L'étude des propriétés de symétrie des vecteurs vrais et des pseudo-vecteurs sera un préalable sur le chemin de l'électromagnétisme.
- Ainsi exprimée en fonction du champ d'excitation magnétique $
\overrightarrow{B}$, la loi de Biot et Savart peut prendre les trois expressions équivalentes, à utiliser selon les besoins :
$\overrightarrow{dB}_M=\dfrac{\mu_0}{4\pi}\cdot\dfrac{I\cdot\overrightarrow{dl}_P\land\overrightarrow{PM}}{||\overrightarrow{PM}||^3}\quad$$,\quad\overrightarrow{dB}_M=\dfrac{\mu_0}{4\pi}\cdot\dfrac{\overrightarrow{j} \cdot d\tau_P\land\overrightarrow{PM}}{||\overrightarrow{PM}||^3}\quad$$,\quad\overrightarrow{dB}_M=\dfrac{\mu_O}{4\pi}\cdot\dfrac{q_P \cdot \overrightarrow{v}\land\overrightarrow{PM}}{||\overrightarrow{PM}||^3}$
-
Dans le vide et uniquement dans le vide, le champ magnétique se représentée aussi bien par le champ d'induction magnétique $
\overrightarrow{B}$ que par le champ d'excitation magnétique $\overrightarrow{H}$, qui se déduisent l'un de l'autre par la simple multiplication par une constante : la constante magnétique encore appelée perméabilité magnétique absolue du vide. -
Dans le vide : $
\mathbf{\overrightarrow{B}=\mu_0\,\overrightarrow{H}}$
! Note sur l'interprétation des champs $\overrightarrow{B}$ et $\overrightarrow{H}$
!
! Nous pouvons interpréter les champs et de la façon suivante :
! Un courant électrique excite magnétiquement l'espace vide, interprété comme un milieu linéaire isotrope ($\overrightarrow{B}\propto \overrightarrow{H}$) parmi d'autres. Sous l'effet de ce champ d'excitation magnétique $\overrightarrow{H}$, le milieu réagit en créant le champ d'induction $\overrightarrow{B}$, qui sera la cause des différents effets induits, dont la force magnétique $\overrightarrow{F}_B = q \; (\overrightarrow{v}\land\overrightarrow{B})$ , partie due au champ magnétique de la force de Lorentz $\overrightarrow{F}_{Lor} = q \; (\overrightarrow{E}+\overrightarrow{v}\land\overrightarrow{B})$
!
! Le vide est caractérisé par le rapport de proportionnalité entre $\overrightarrow{B}$ et $\overrightarrow{H}$, appelé constante magnétique ou encore perméabilité magnétique du vide notée $\mu_0$.
!! Pour aller plus loin :
!! Nous verrons lors de l'étude de la magnétostatique dans les milieux magnétiques, que sous excitation d'un champ d'excitation magnétique $\overrightarrow{H}$, le milieu développera une aimantation $\overrightarrow{M}$ (grandeur physique de même dimension physique que $\overrightarrow{H}$ donc d'unité SI $A\cdot m$) qui complètera $\overrightarrow{H}$ pour donner le champ d'induction magnétique $\overrightarrow{B}$ :
!! $\overrightarrow{B}=\mu_0\,(\overrightarrow{H}+\overrightarrow{M})\quad$ , soit $\quad\overrightarrow{H}=\dfrac{\overrightarrow{B}}{\mu_0}+\overrightarrow{M}$.
!!
!! Un milieu magnétique linéaire isotrope sera caractérisé des vecteurs $\overrightarrow{B}$ et $\overrightarrow{H}$ simplement proportionnels, tels que :
!! $\overrightarrow{B}=\mu\overrightarrow{H}=\mu_0\mu_r\overrightarrow{H}\quad[eq.2].$
!! où la perméabilité absolue $\mu$ comme la perméabilité relative $\mu_r$ du milieu caractérise son comportement magnétique.
!!
!! Si le milieu magnétique est linéaire ET anisotrope, $[eq.2]$ restera vérifiée, mais $\mu$ et $\mu_r$ seront de nature tensorielle.
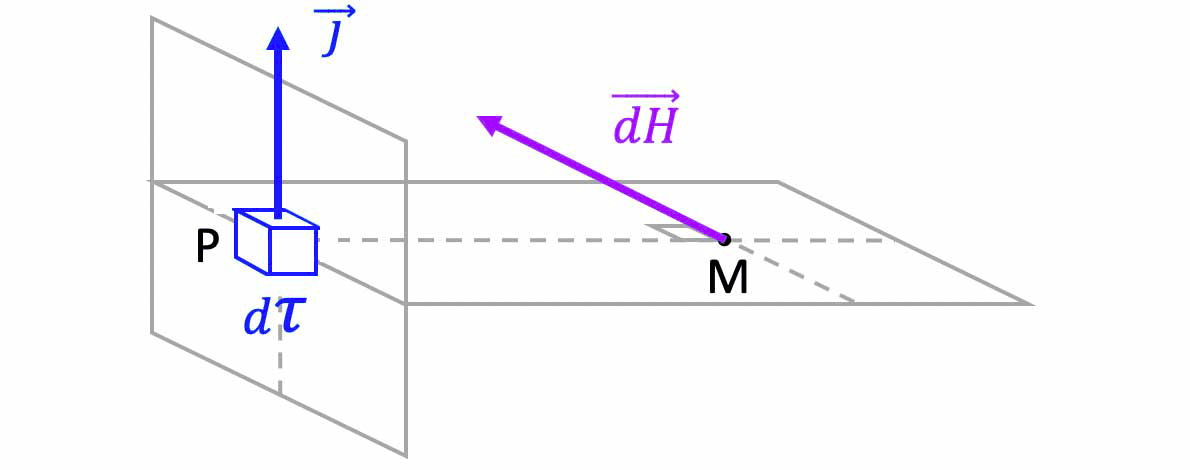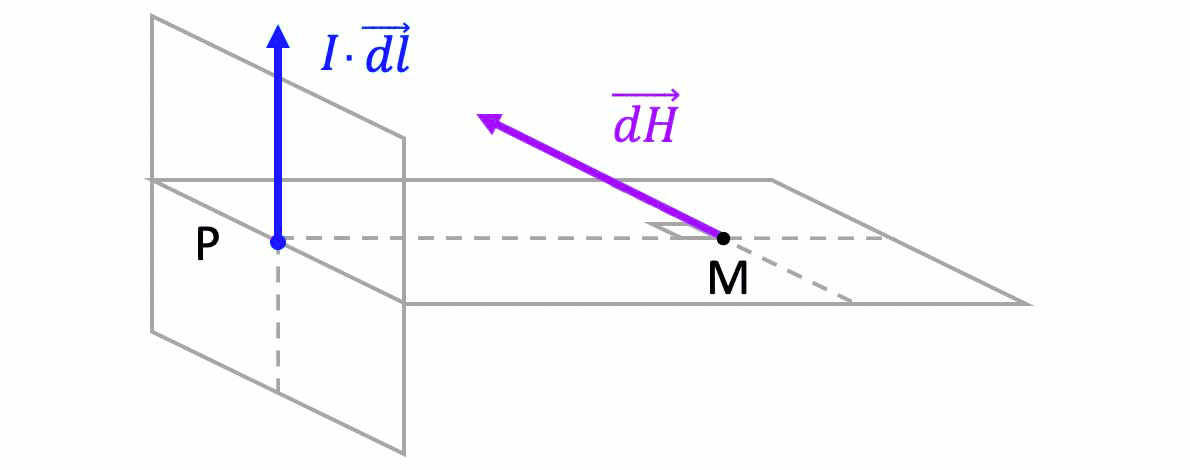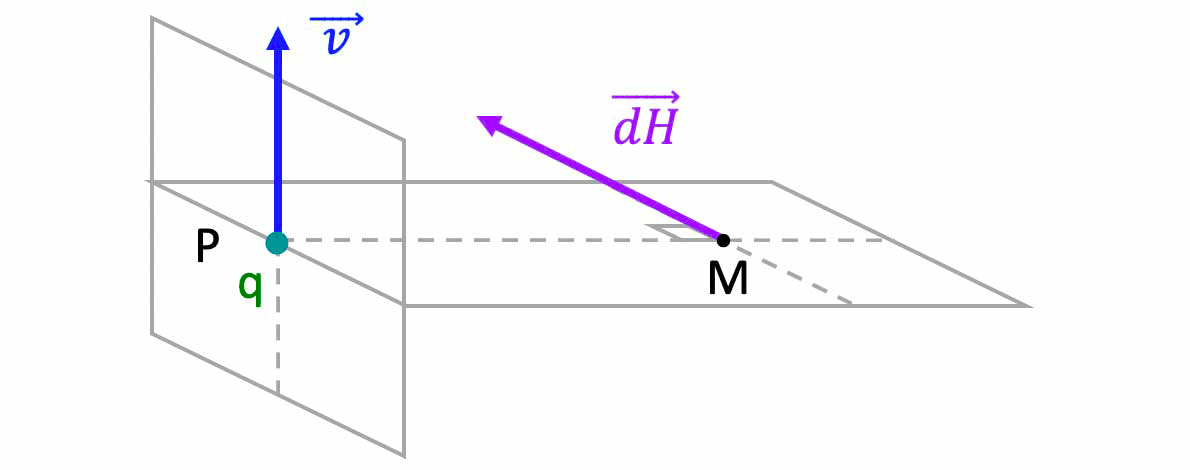
- La loi de Biot et Savart exprimée en fonction du champ d'excitation magnétique $
\overrightarrow{H}$ ) s'écrit :
$\mathbf{\overrightarrow{dH}_M=\dfrac{1}{4\pi}\cdot\dfrac{I\cdot\vec{dl}_P\land\overrightarrow{PM}}{||\,\overrightarrow{PM}\,||^{\,3}}}$
soit encore :
$\mathbf{\overrightarrow{dH}=\dfrac{1}{4\pi}\cdot\dfrac{I\cdot\overrightarrow{dl}\land\overrightarrow{r}}{r^3}=\dfrac{1}{4\pi}\cdot\dfrac{I\cdot\overrightarrow{dl}\land\overrightarrow{e_r}}{r^2}}$, avec $\overrightarrow{r}=r\;\overrightarrow{e_r}$ et $r>0$, l'élément de courant étant localisé en $\overrightarrow{r}=\overrightarrow{0}$,
- L'équation au dimension du champ d'excitation magnétique $
\overrightarrow{H}$ peut être obtenue à partir de cette loi de Biot et Savard :
$[H]=\dfrac{I \cdot L \cdot L}{L^3}= I \cdot L^{2-3} = I \cdot L^{-1}$
L'unité du champ d'excitation magnétique est l'Ampère par mètre, $\mathbf{A\cdot m^{-1}}$, dans le système internationale de mesure (SI).
! Note :
! * Séparer des charges de signes opposées créé un *champ électrique $\overrightarrow{E}$ * dont l'unité SI est le Volt par mètre, $V\cdot m^{-1}$.
! * Générer des courants électriques créé un *champ d'excitation magnétique $\overrightarrow{H}$ * dont l'unité SI est l'Ampère par mètre, $A\cdot m^{-1}$.
!! Pour aller plus loin sur la nature de $\overrightarrow{H}$ :
!! Pour les mêmes raisons que l'induction magnétique , l'excitation magnétique $\overrightarrow{H}$ est un pseudo vecteur (ou vecteur axial).