courses/12.temporary_ins/magnetostatics-magnetic-media/overview/cheatsheet.fr.md

title	published	routable	visible
Magnétostatique des milieux magnétiques	true	true	false

!!!! COURS EN CONSTRUCTION :
!!!! Publié mais invisible : n'apparait pas dans l'arborescence du site m3p2.com. Ce cours est en construction, il n'est pas validé par l'équipe pédagogique à ce stade.
!!!! Document de travail destiné uniquement aux équipes pédagogiques.

Équilibre magnétostatique dans les milieux magnétiques

Qu'est ce qu'un milieu magnétique ?

Tous les atomes contiennent des électrons en mouvements qui crééent des champs magnétiques par un effet quantique.

Les atomes des matériaux magnétiques agissent comme des dipoles magnétiques.

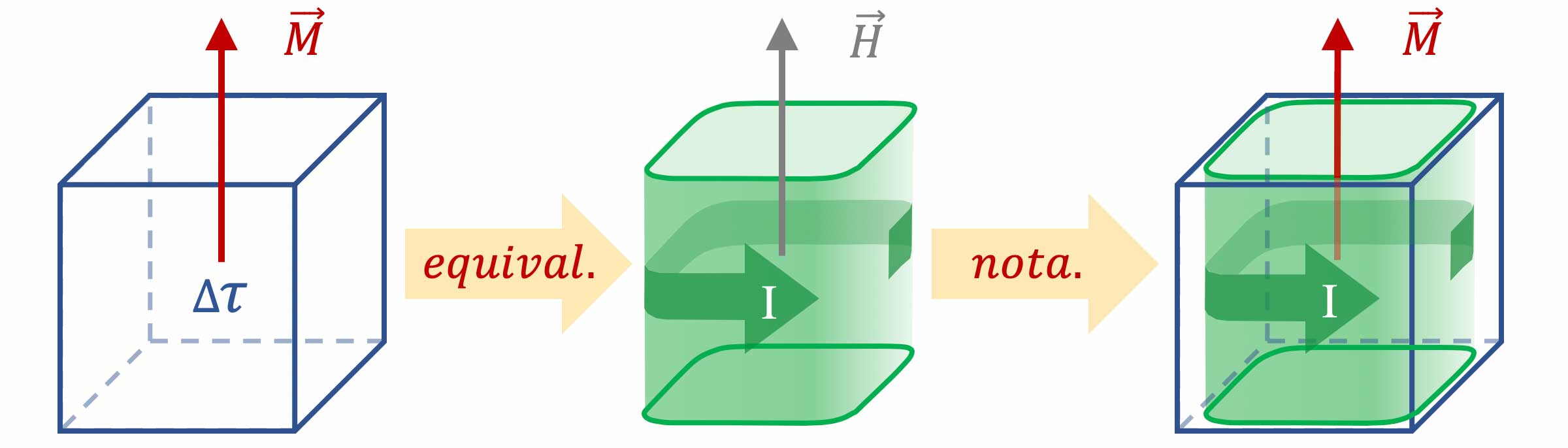
Un petit volume de matière aimanté présente les mêmes caractéristiques qu'un moment magnétique associé à une boucle de courant.

• Il créé un champ d'induction magnétique $\mathbf{\vec{B}}$ identique.

• En présence d'un champ magnétique, il subit le même couple et la même force.

Les milieux magnétiques sont caractérisés par l'existence de moments dipolaires magnétiques individuels $\vec{m}_i$ associés aux atomes, ions ou molécules qui les composent.

Boucle élémentaire de courant = tourbillon = dipôle magnétique

Qu'est-ce qu'un moment magnétique $\overrightarrow{m}$

• un vecteur $\mathbf{\overrightarrow{m}}$ qui caractérise un dipôle magnétique.

• moment magnétique $\mathbf{\overrightarrow{m}=I\cdot \overrightarrow{s}}$ : $I$ est l'intensité dans la boucle plane de courant qui délimite une surface d'aire $s$. La surface $s$ est représentée par son vecteur surface $\overrightarrow{s}$ orienté selon la règle de la main droite, lorsque le sens positif sur la boucle est le sens de circulation du courant $I$.

• unité SI : $\mathbf{A\,m^2}$

• Intérêt de $\overrightarrow{m}$ : le champ magnétique créé à grande distance (devant sa taille) par un dipôle magnétique s'exprime simplement en fonction de $\overrightarrow{m}$ :
  
  $\overrightarrow{B}=\dfrac{\mu_0}{4\,\pi}\cdot\left(3\overrightarrow{r}\cdot\dfrac{\overrightarrow{m}\cdot\overrightarrow{r}}{r^5}-\dfrac{\overrightarrow{m}}{r^3}\right)$

Quels sont les phénomènes à l'origine de moments magnétiques ?

Les atomes comprend des protons et électrons en mouvement, et à ce titre ils peuvent être source de champs magnétiques. Leurs mouvements confinés les font agir comme des dipôles magnétique.

A cette échelle atomique, la description classique en terme de particules chargées possédant une position, une vitesse et une trajectoire est très réductrice et fausse, la description correcte nécessite la physique quantique.

Moment magnétique orbital

• C'est le moment magnétique créé par les électrons sur leurs orbitales atomiques.

• S'il la description ne peu être que quantique, à ce niveau une vision classique de ce phénomène reprenant le modèle atomique planétaire de Bohr, peut-être utile pour une perception intuitive, et faire le lien avec spires ou solénoïdes macroscopiques parcourus par des courants de conduction.

• Imaginons un électron classique de masse $m_e$ se déplaçant à la vitesse $v_e$ sur une orbite circulaire de rayon $r_e$. Cet électron équivaut à une petite boucle de courant. Dans un fil électrique (on néglige sa section), l'intensité du courant est la charge qui traverse chaque seconde un point donné de ce fil. Appliquons ceci à notre électron.
  
  La circonférence de l'orbite de rayon $r_e$ est $2\pi r_e$. L'électron parcourt cette orbite en un temps $\delta\tau=\dfrac{2\pi r_e}{v_e}$. Il traverse donc un point de cette orbite $\dfrac{v_e}{2\pi r_e}$ fois par seconde. Comme il porte une chargé électrique $-e$, cette situation correspond à une petite boucle plane de courant, de section $s=\pi\,r^2$ et d'intensité $I=\dfrac{e\,v_e}{2\pi r_e}$. Le moment magnétique de cette petite boucle de courant est :
  
  $\mathbf{\overrightarrow{m_e}=I\cdot\overrightarrow{s}}$$\;=\dfrac{e\,v_e}{2\pi r_e}\times\pi\,r_e^2\cdot\overrightarrow{u_s}$$\;\mathbf{=\dfrac{e\,r_e\,v_e}{2}\cdot\overrightarrow{u_s}}$
  
  où $\overrightarrow{u_s}$ est le vecteur unitaire perpendiculaire au plan de l'orbite, orienté selon la règle de la main droite lorsque le sens positif pris sur l'orbite est le sens du courant (donc le sens opposé au mouvement de l'électron).

• Ce moment magnétique peut se réécrire :
  
  $\overrightarrow{m_e}=\dfrac{e\,r_e\,v_e}{2}\cdot\overrightarrow{u_s}=-\dfrac{e}{2\,m_e}\cdot(-m_e\,r_e\,v_e\;\overrightarrow{u_s})$$\;=-\dfrac{e}{2\,m_e}\cdot(+m_e\,r_e\,v_e\;\overrightarrow{u_e})$
  avec $\overrightarrow{u_e}=-\overrightarrow{u_s}$
  pour faire apparaître le moment cinétique $\mathbf{\overrightarrow{L_e}=m_e\,r_e\,v_e\;\overrightarrow{u_e}}$ de l'électron sur son orbite, où $\overrightarrow{u_e}$ est le vecteur unitaire perpendiculaire au plan de l'orbite, orienté selon la règle de la main droite lorsque le sens positif pris sur l'orbite est le sens du mouvement de l'électron (sens inverse du courant qu'il créé). Au total :
  
  $\mathbf{m_e=-\dfrac{e}{2\,m_e}\cdot\overrightarrow{L_e}}$

Moment magnétique de spin

• L'électron possède un moment magnétique qui lui est propre, indépendant de son mouvement orbitale. Ce moment magnétique est purement quantique et est appelé moment magnétique de spin.

• Une image classique serait d'associer le moment magnétique de spin à la rotation de l'électron sur lui-même. Si nous modélisons l'électron par une petite sphère, que sa charge est répartie sur sa surface sphérique et qu'il tourne sur lui-même, alors nous aurions l'équivalent de boucles circulaires de courant de même axe et de rayons variables s'adaptant à la surface de la sphère. Même en donnant une extension spatiale à l'électron (si l'électron peut être caractérisée par une taille, celle-ci doit être inférieure à $10^{-18}\,m$`), le moment magnétique de l'électron nécessiterait qu'un point à sa surface équatoriale se déplace à une vitesse bien supérieure à la vitesse de la lumière, ce que la relativité et l'expérience interdit.

Qu'est-ce que le vecteur aimantation $\overrightarrow{M}$ ?

• Au sein de la matière les dipoles magnétiques sont contenu dans un volume de dimension atomique.

• Un "point" d'observation ou de caractérisation représente un volume de dimension mésoscopique.

• Un volume mésoscopique est un volume :
  ▪  de taille grande devant l'échelle atomique caractéristique des entités élémentaires ou des variations des champs induits, afin de définir des moyennes spatiales pertinentes.
  
  ▪  de taille quasi-ponctuelle devant l'échelle de description macroscopique de la matière, de façon que les moyennes spatiales définies et mesurées varient continuement
  

• Le vecteur aimantation $\overrightarrow{M}$ :
  ▪  caractérise l'état d'aimantation de chaque volume mésoscopique $\Delta\tau$.
  ▪  c'est le vecteur densité de moment magnétique :
  
  $\displaystyle\mathbf{\overrightarrow{M}=\dfrac{1}{\Delta\tau}\sum_{i\in\Delta\tau}\overrightarrow{m_i}}$

• unité SI : $\mathbf{A\;m^{-1}}$
  

• Au sein d'un matériau :
  ▪  $\mathbf{\overrightarrow{M}=\overrightarrow{cst}}$ $\Longrightarrow$ aimantation uniforme.
  ▪  $\mathbf{\overrightarrow{M}}$ varie continument $\Longrightarrow$ aimantation non uniforme.

En absence d'un champ magnétique extérieur, un matériau contient-il des dipôles magnétiques ?

La matière est composée d' atomes qui peuvent posséder chacun un moment magnétique nul ou un moment magnétique non nul. Le moment magnétique de chaque atome dépend de la position et des moments magnétiques des atomes voisins, de la température, des champs magnétiques appliquées de l'extérieur.

En absence d'un champ magnétique extérieur, un matériau est t-il aimanté ?

• Dans la plupart des atomes, les moments magnétiques orbitaux et de spins s'annulent et donc le moment magnétique atomique est nul. Si cela n'est pas le cas, du fait de l'agitation thermique les moments magnétiques atomiques ont des orientations aléatoires, ce qui confère une aimantation nul au matériau auquel ils appartiennent.

• Dans certains matériaux appelés matériaux ferromagnétiques, des interactions interatomiques conduisent à un alignements d'atomes voisins. Ces matériaux présentent alors une aimantation permanente. Au-delà d'une température élevée qui dépend du matériau et appelée température de Curie, l'agitation thermique peut détruire l'alignement spontané des atomes, auquel cas l'aimantation disparaît.

Comment un champ magnétique extérieur aimante un matériau ?

• Un champ d'induction magnétique uniforme à l'échelle d'un dipôle magnétique
  $\Longrightarrow\;$ couple non nul qui tend à orienter le dipôle en direction du champ.
  $\Longrightarrow\;$ force résultante nulle sur le dipôle.

• L'application d'un champ magnétique extérieur $\overrightarrow{B_{ext}}$ dans un volume mésoscopique $\Delta\tau$
  $\Longrightarrow\;$ création de dipôles d'orientation moyenne en direction de $\overrightarrow{B_{ext}}$
  ou $\Longrightarrow\;$ réorientation des dipôles préexistants vers une direction moyenne selon $\overrightarrow{B_{ext}}$
  
  

• L'application d'un champ d'induction magnétique extérieur stationnaire
  

$\Longrightarrow\;$ établissement d'un équilibre où le matériau a une aimantation non nulle

Un milieu aimanté est-il équivalent à une densité volumique de courants liés ?

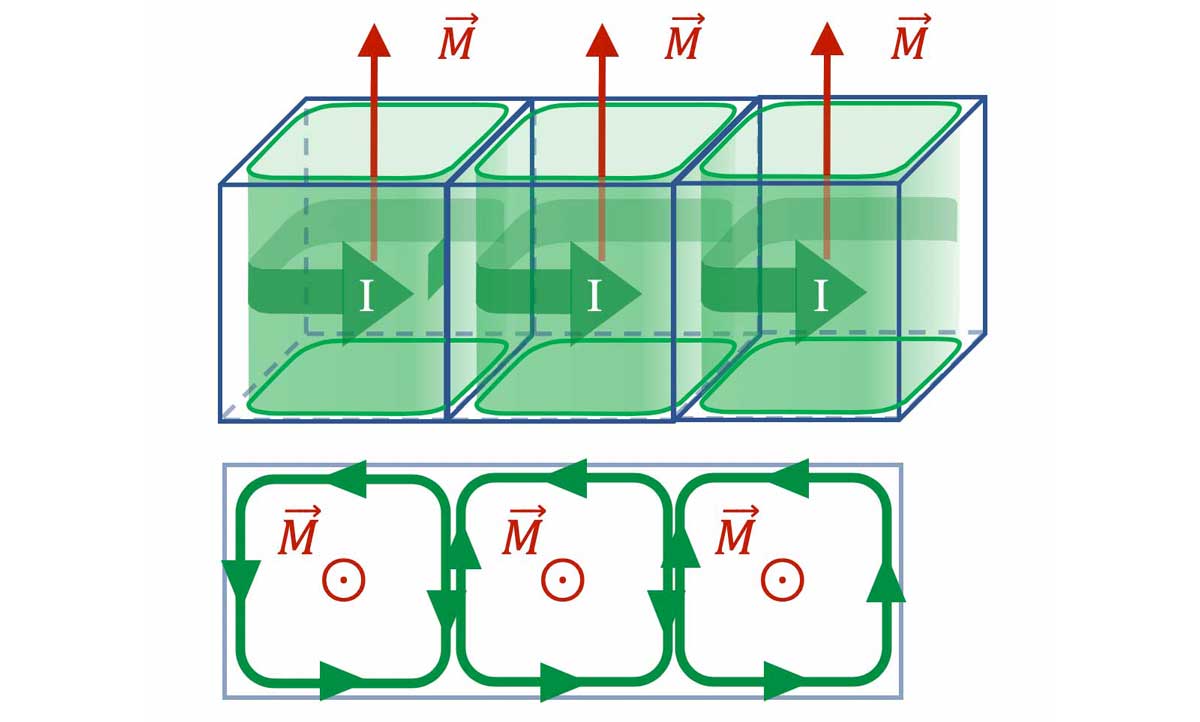
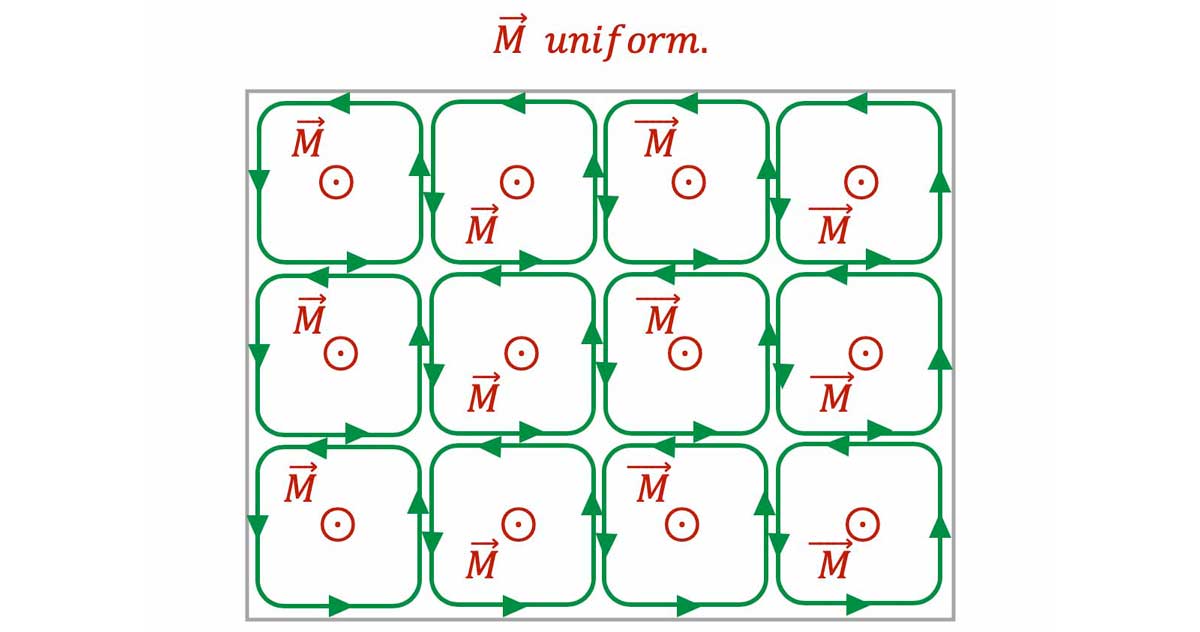
L'aimantation est uniforme

• Aimantation uniforme $\mathbf{\Longrightarrow\overrightarrow{M}(\overrightarrow{r})=\overrightarrow{const}}$
  $\Longrightarrow$ pas de variation de $\overrightarrow{M}$ d'un volume mésoscopique $\Delta\tau$ à un autre.
  $\Longrightarrow$ pas de variation de $\overrightarrow{M}$ si le volume mésoscopique $\Delta\tau$ considéré se déplace d'une fraction de sa longueur. poly_

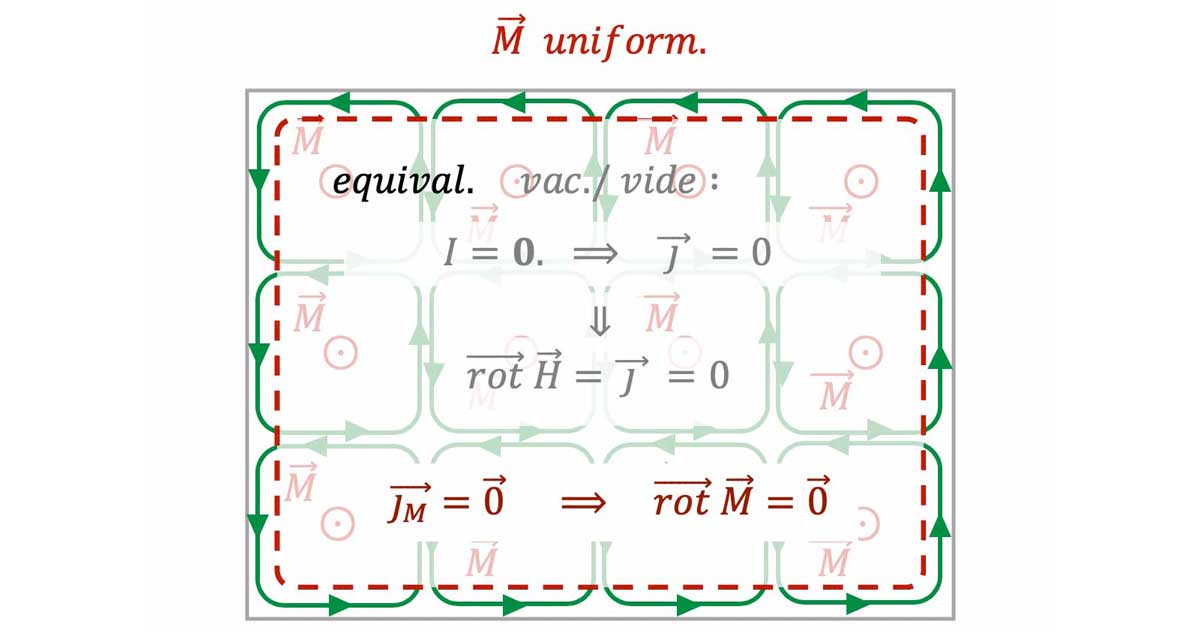
• Aimantation uniforme $\Longrightarrow$ pas de courant d'aimantation en volume
  $\mathbf{\overrightarrow{M}=\overrightarrow{const}}$$\quad\Longrightarrow\quad\mathbf{\overrightarrow{j_M}=0}$.

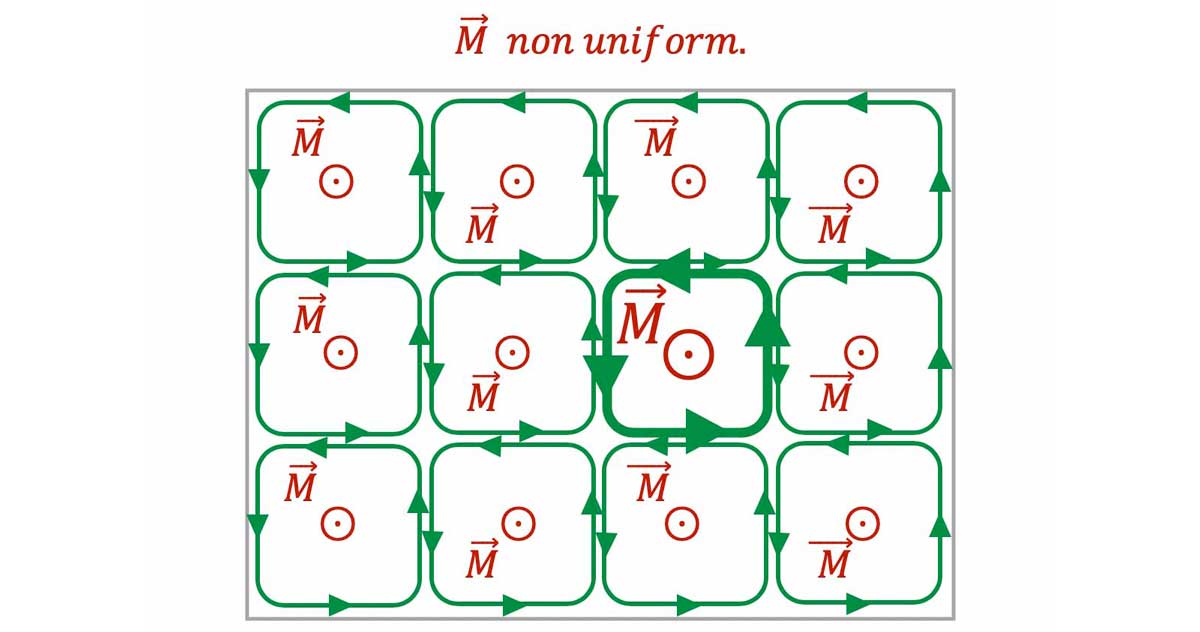
L'aimantation est non uniforme

• Aimantation non uniforme $\Longrightarrow\mathbf{\overrightarrow{M}}$ est fonction de la position $\mathbf{\overrightarrow{r}}$
  $\Longrightarrow$ variation de $\overrightarrow{M}$ d'un volume mésoscopique $\Delta\tau$ à un autre.
  $\Longrightarrow$ variation de $\overrightarrow{M}$ si le volume mésoscopique $\Delta\tau$ considéré se déplace d'une fraction de sa longueur. poly_

• Pour revenir au cas précédent, la rotationnel d'une aimantation uniforme est nul. Nous en déduisons un fait et une relation très importante :

En tout point d'un matériau, le vecteur densité volumique de courant d'aimantation $\mathbf{\overrightarrow{j}_M}$ est égal au rotationnel du vecteur aimantation en ce point.

$\mathbf{\overrightarrow{j}_M=\overrightarrow{rot}\,\overrightarrow{M}}$

Un milieu d'aimantation $\overrightarrow{M}$ uniforme est-il équivalent à une densité surfacique de courants liés ?

• Le vecteur densité surfacique de courant d'aimantation $\mathbf{\vec{j}_{Msu.}}$ en surface est :
  
  $\mathbf{\overrightarrow{j}_{Msu.}=\overrightarrow{M}\wedge\overrightarrow{u}_{su.}}$
  
  où $\overrightarrow{u}_{su.}$ est le vecteur unitaire perpendiculaire à la surface, et orienté de l'intérieur vers l'extérieur du volume aimanté.

Que devient le théorème d'Ampère dans un matériau magnétique ?

Le théorème d'Ampère en fonction de $\overrightarrow{B}$.

Dans le vide, l'équation de Maxwell reliant le champ magnétique à ses causes est

$\mathbf{\overrightarrow{rot}\,\overrightarrow{B}=\mu_0\,\overrightarrow{j}}$ ou $\mathbf{\overrightarrow{rot}\,\overrightarrow{H}=\overrightarrow{j}}$

où $\overrightarrow{j}$ est le vecteur densité volumique de courant à l'origine du champ magnétique)

! Important : ! ! Dans le vide le champ d'induction magnétique $\vec{B}$ et le champ d'excitation magnétique $\vec{H}$ sont reliés l'un à l'autre par le simple rapport de proportionnalité scalaire $\mu_0$ tel que : ! ! $\vec{B}=\mu_0\;\vec{H}\quad$ ! ! où $\mu_0$ est la constante magnétique, encore appelée perméabilité magnétique du vide, d'unité et de valeur dans le S.I.: ! !$\mu_0 = 1.256\,6... \cdot 10^{-6}\; kg\,m\,A^{-2}\,s^{-2} \;=4\pi \cdot 10^{-7} \;T\,m \,A^{-1}$ ! ! Dans le vide $\vec{B}$ et $\vec{H}$ sont deux représentations d'un même champ, le champ magnétique*.

Dans la matière, la détermination du champ d'induction magnétique $\mathbf{\vec{B}}$ s'exprime de façon identique à celle du vide, mais en considérant deux types de courant :

• des courants de conductions, courant de particules libres, de vecteur densité volumique de courant $\mathbf{\vec{j_{lib}}}$.
• des courants associés à l'aimantation de la matière, de vecteur densité volumique de courant $\mathbf{\vec{j_M}}$.

Nous avons donc :

$\overrightarrow{rot}\,\overrightarrow{B}=\mu_0\,\left(\overrightarrow{j_{lib}}+\overrightarrow{j_M}\right)$

soit, avec l'égalité $\overrightarrow{j_M}=\overrightarrow{rot}\,\overrightarrow{M}$

Théorème d'Ampère en fonction de $\overrightarrow{H}$ redéfini dans la matière

L'expression

$\overrightarrow{rot}\,\overrightarrow{B}=\mu_0\,\left(\overrightarrow{j_{lib}}+\overrightarrow{rot}\,\overrightarrow{M}\right)$

peut se réécrire :

$\overrightarrow{rot}\,\overrightarrow{B}-\mu_0\,\overrightarrow{rot}\,\overrightarrow{M}=\mu_0\,\overrightarrow{j_{lib}}$

soit :

$\mathbf{\overrightarrow{rot}\,\left(\dfrac{\overrightarrow{B}}{\mu_0}-\overrightarrow{M}\right) =\overrightarrow{j_{lib}}}$

Dans la matière, le champ d'excitation magnétique $\mathbf{\vec{H}}$ se redéfinit comme :

$\mathbf{\vec{H}=\dfrac{\vec{B}}{\mu_0}-\vec{M}}$

et il vérifie le théorème d'Ampère :

$\mathbf{\overrightarrow{rot}\,\overrightarrow{H}=\overrightarrow{j_{lib}}}$

L'avantage de cette expression est que n'apparait seulement que le vecteur densité voulmique de courants libres, courants de conduction mesurables.

! Important : ! ! Cette définition de $\vec{H}$ dans la matière est cohérente avec l'expression de $\vec{H}$ dans le vide où par définition il n'y à pas de matière donc pas d'aimantation possible. ! ! $\overrightarrow{M}=0\quad\Longrightarrow\overrightarrow{B}=\mu_0\,\overrightarrow{H}$

!!!! Attention : !!!! !!!! Dans la matière et contrairement au vide, les champs $\vec{B}$ et $\vec{H}$ sont deux champs distincts. !!!! !!!! En effet, pour un même champ $\vec{H}$, $||\vec{M}||-||\vec{H}||$ varie en valeur selon les matériaux, peut être négatif ou positif. Dans le cas d'un matériau anisotrope, les orientations de $\vec{H}$ et $\vec{M}$ peuvent être différentes, ce qui implique que les champs $\vec{B}$ et $\vec{H}$ ne sont pas parallèles.

• Si un volume mésoscopique est plongé dans un champ d'excitation magnétique $\vec{H}$, l'aimantation induite $\vec{M}$ est une fonction de $\vec{H}$ qui dépend du milieu : $\mathbf{\overrightarrow{M} = \overrightarrow{M}(\overrightarrow{H})}$

• Si le milieu est linéaire (L)
  $\Longrightarrow\; \mathbf{||\overrightarrow{M}|| \propto ||\overrightarrow{H}||}$ : les normes des vecteurs $\overrightarrow{M}$ et $\overrightarrow{H}$ varient proportionnellement. $

• Si le milieu est homogène et isotrope (HI)
  $\Longrightarrow\; \mathbf{\overrightarrow{M} // \overrightarrow{H}}$ : les vecteurs $\overrightarrow{M}$ et $\overrightarrow{H}$ ont même direction.

• Si le milieu est linéaire, homogène et isotrope (LHI)
  $\Longrightarrow\; \mathbf{\overrightarrow{H} \propto \overrightarrow{M}}$ : les vecteurs $\overrightarrow{M}$ et $\overrightarrow{H}$ sont proportionnels.

Qu'est-ce que la susceptibilité magnétique d'un milieu ?

• Pour un milieu homogène, isotrope et linéaire (LHI), la susceptibilité magnétique notée $\mathbf{\chi_m}$ est le rapport de proportionnalité entre $\overrightarrow{M}$ et $\overrightarrow{H}$
  
  $\chi_m=\dfrac{\overrightarrow{M}}{\overrightarrow{H}}$$\Longrightarrow\;\mathbf{\overrightarrow{M}=\chi_m\, \overrightarrow{H}}$

• unité SI : sans unité (scalaire pur)
  

Qu'est-ce que la perméabilité (magnétique) relative $\mu_r$ d'un matériau ?

Pour un milieu linéaire, homogène et isotrope (LHI) , la perméabilité (magnétique) relative est le nombre réel $\mu_r$ qui vérifie :

$\mathbf{\overrightarrow{B}=\mu_0\,\mu_r\,\overrightarrow{H}}$ $\;=\mu_O\cdot\left(\overrightarrow{H}+\overrightarrow{M}\right)$

Lien entre perméabilité relative et susceptibilité magnétique

Pour un milieu linéaire, homogène et isotrope (LHI) : $\overrightarrow{M}==\chi_m\, \overrightarrow{H}$

Donc :

$\overrightarrow{B}=\mu_0\cdot\left(\overrightarrow{H}+\overrightarrow{M}\right)$

$\overrightarrow{B}=\mu_0\cdot\left(1+\chi_m\right) \overrightarrow{H}=\mu_0\,\mu_r\,\overrightarrow{H}$

ce qui donne

$\mathbf{\mu_r=1+\chi_m}$