9.1 KiB
| title | published | routable | visible |
|---|---|---|---|
| <nil> | false | false | false |
!!!! ATTENTION ! : statut de ce cours : non validé, en construction
Quelle propriété doit satisfaire un système optique imageur "idéal" ?
-
Système optique imageur : système macroscopique.
(de taille caractéristique grande devant la longueur d'onde de la lumière incidente). -
Tous rayons issus d'un même point object A incidents en tout point d'un système imageur, après interaction avec le système, doivent converger en un même point image B:
Cette propriété s'appelle le stigmatisme. $\Longrightarrow$ le stigmatisme est une propriété macroscopique. -
En tout point d'un système optique, la déviation d'un rayon incident dépend du plan et de l'angle d'incidence en ce point et suit la loi de la réflexion ou le loi de la réfraction :
$\Longrightarrow$ la déviation d'un rayon incident est une phénomène local (microscopique). -
$
\Longrightarrow$ le stigmatisme, propriété macroscopique, émerge de la forme macroscopique du système optique imageur.
(courbure de la surface d'un dioptre ou d'un miroir).
Quelles courbures considérer pour étudier le stigmatisme ?
- Pour que localement les lois de la réflexion et de la réfraction s'appliquent,
la surface doit être localement assimilable à un plan.
$\Longrightarrow$ en chaque point, le rayon de courbure $R_c$ de la surface doit être grand devant la longueur d'onde de la lumière incidente : $R_c \gg \lambda$.
$\Longrightarrow$ la taille caractéristique $d$ des défauts de surface doit être petite devant la longueur d'onde : $d \ll \lambda /10$.
-
Pour des raisons de facilité de réalisation technique et donc de côut de fabrication, les éléments optiques simples ont des surfaces planes ou sphériques :
$\Longrightarrow$ les éléments optiques simples seront :
- le miroir plan.
- les miroirs sphériques.
- les dioptres plans.
- le dioptres sphériques. -
Bien que un peu plus difficile à réaliser techniquement et à étudier analytiquement, le miroir parabolique est important car il est "plus stigmatique" que les miroirs sphériques, et donc est largement utilisé en optique.
Un dioptre sphérique est-il un système stigmatique ?
-
dioptre = surface séparant deux milieux d'indices de réfraction différents .
-
Chaque rayon issu d'un même point objet, est dévié en chaque point du dioptre selon des conditions purement locales (plan et angle d'incidence et loi de Snell-Descartes) :
$\Longrightarrow$ aucune raison que les rayons émergeants convergent en un point image.
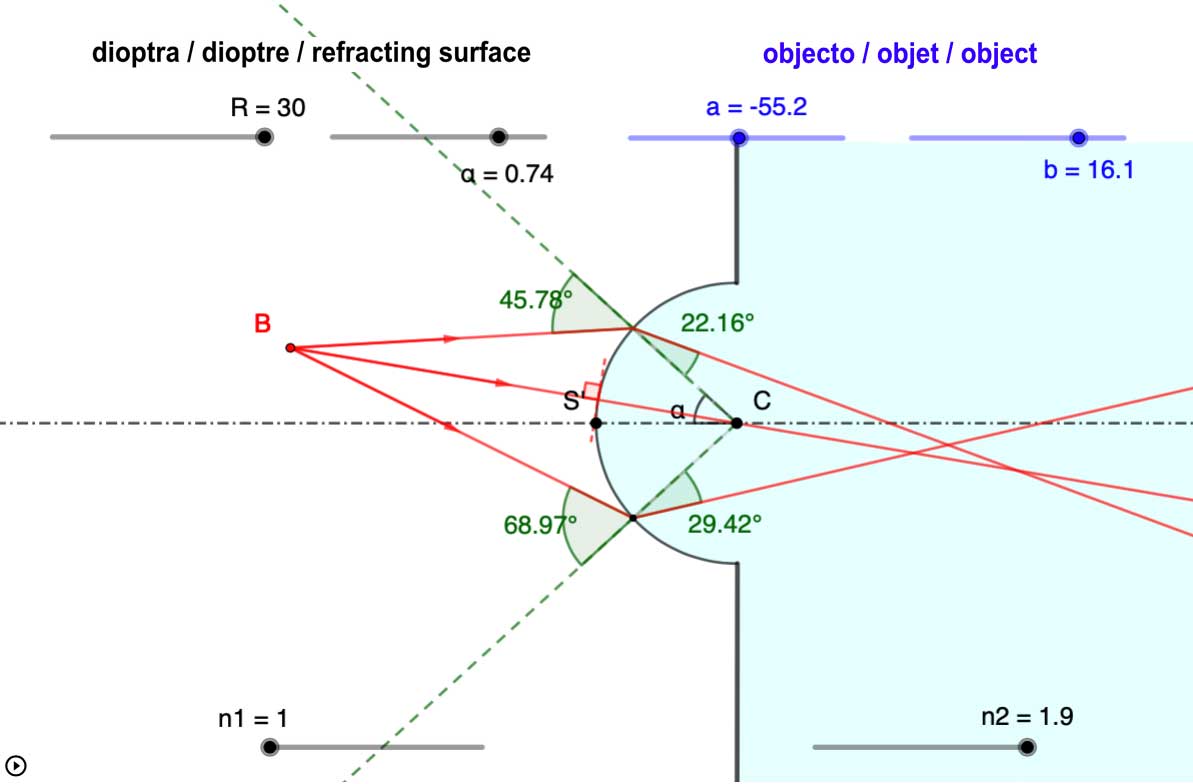
Figure 2 : en chaque point d'un dioptre, la déviation du rayon lumnieux incident obéit à la loi de Snell-Descartes.
! Rappel loi de Snell-Descartes :
! $n_1 \cdot sin(i_1)=n_2 \cdot sin(i_2)$
! $i_1$ est l'angle d'incidence et $i_2$ l'angle de réfraction, , notés
! par rapport à la normale à la surface au point d'impact.
- En chaque point d'un dioptre sphérique, la réfraction d'un rayon lumineux suit
la loi de Snell-Descartes qui s'applique selon des conditions locales propres
à chaque point :
$\Longrightarrow$ aucune raison à l'émergence d'un comportement d'ensemble qui serait "tous les rayons réfractés ou les droites qui les prolongent convergent en un même point".
$\Longrightarrow$ un dioptre sphérique est un élément optique non stigmatique.
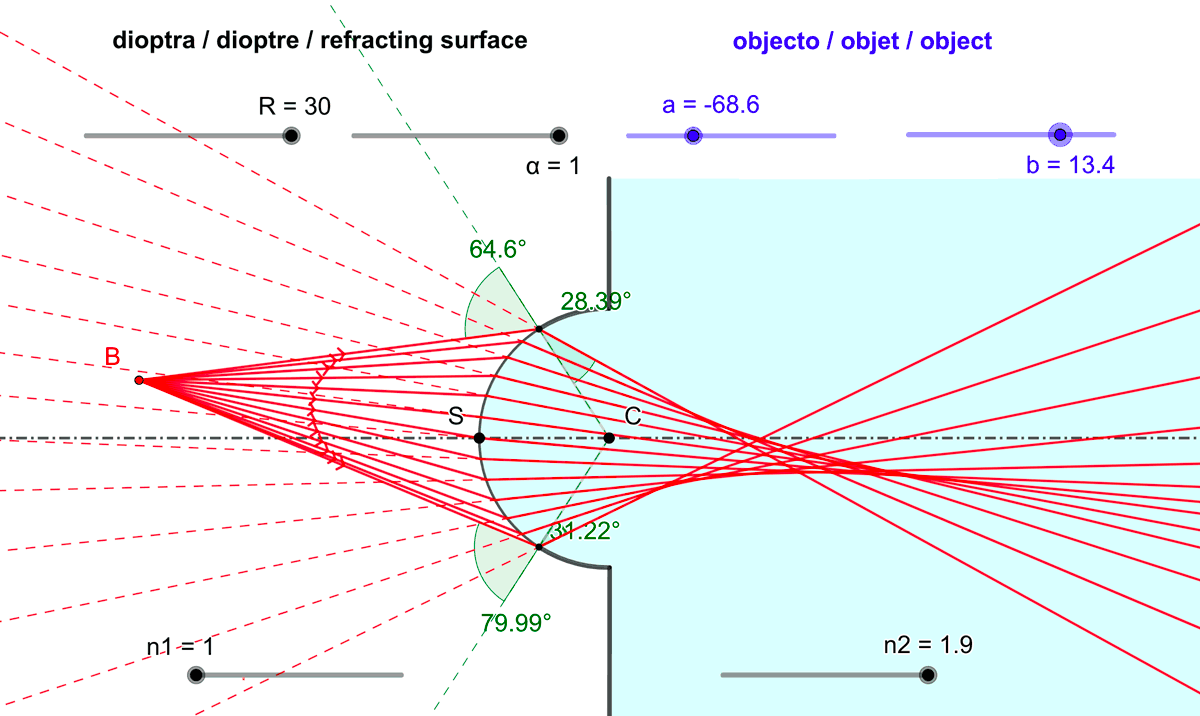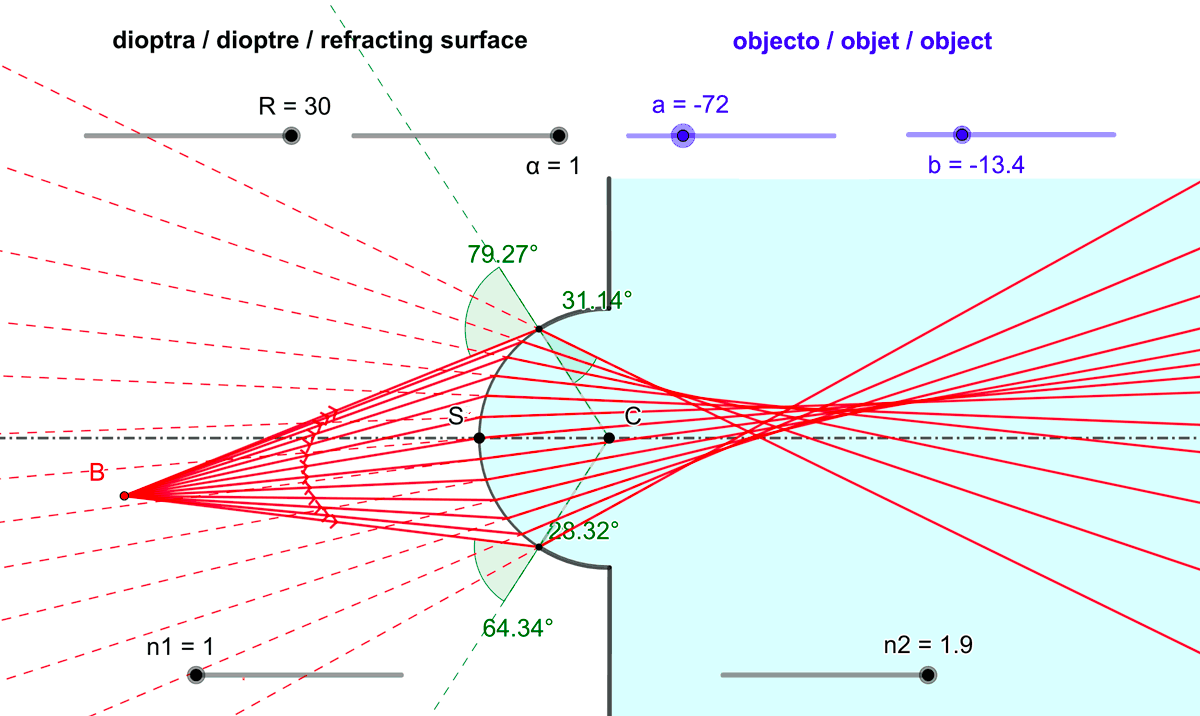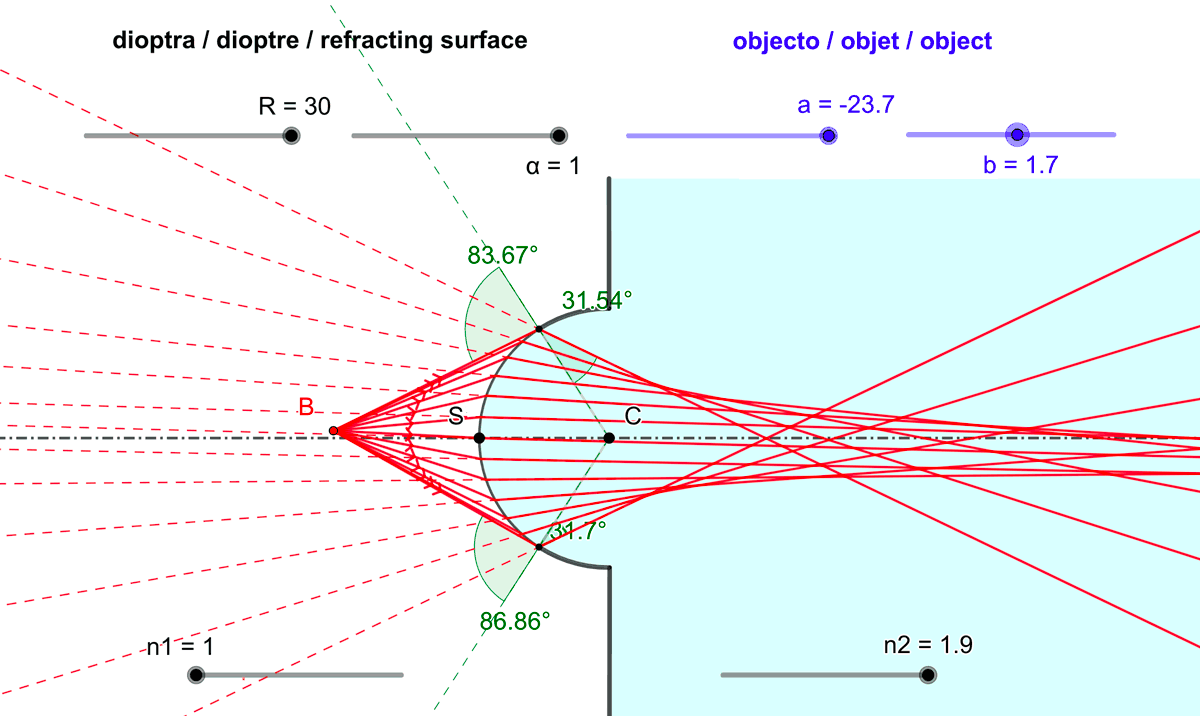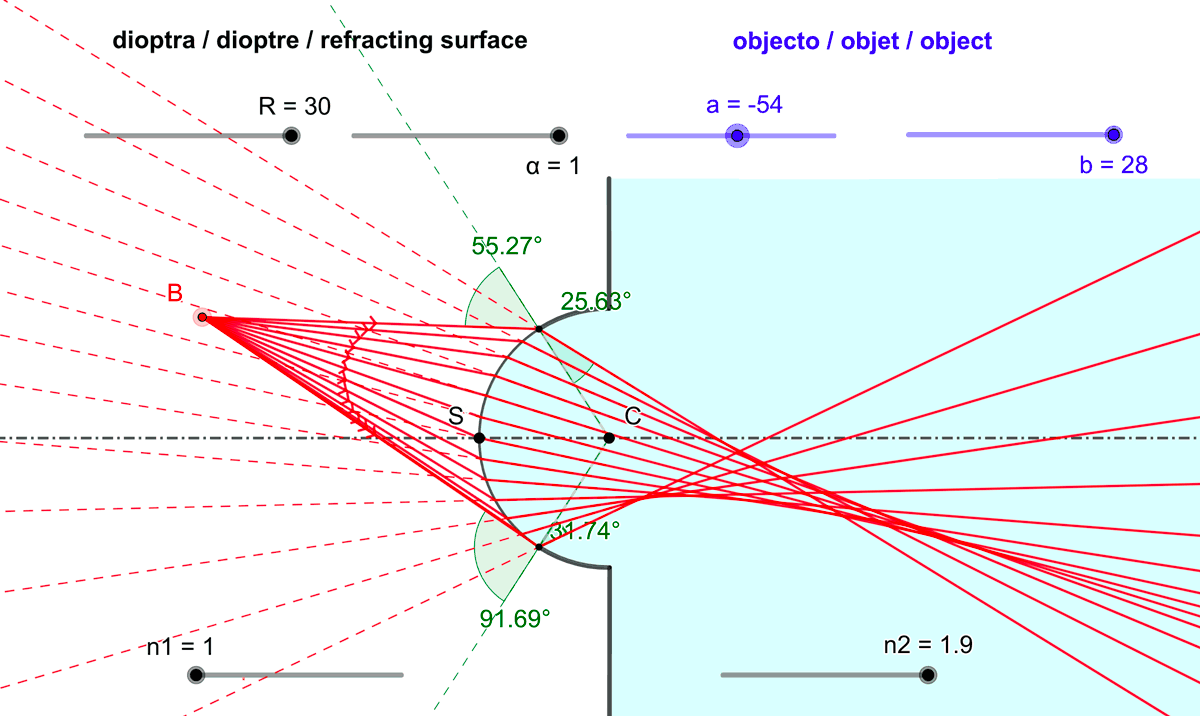
Figure 3 : Les rayons lumineux (ou les droites qui les prolongent) issus d'un point objet et réfractés
à la traversée d'un dioptre sphérique ne convergent en général pas en un point unique :
Un dioptre sphérique est non stigmatique.
Dans quelles conditions un dioptre sphérique peut-il être "presque" stigmatique ?
- "presque" stigmatique = quasi-stigmatique.
On parle de stigmatisme approché.
Le stigmatisme d'un dioptre sphérique s'améliore en limitant le faisceau aux rayons
présentant des angles d'incidence $i_1$ faibles. Pour réaliser cette conditions il faut :
- limiter l'angle d'ouverture du dioptre sphérique (l'angle $
\alpha$ sur la figure 4).
Ceci peut être réalisé en mettant un diaphragme centré sur l'axe optique.
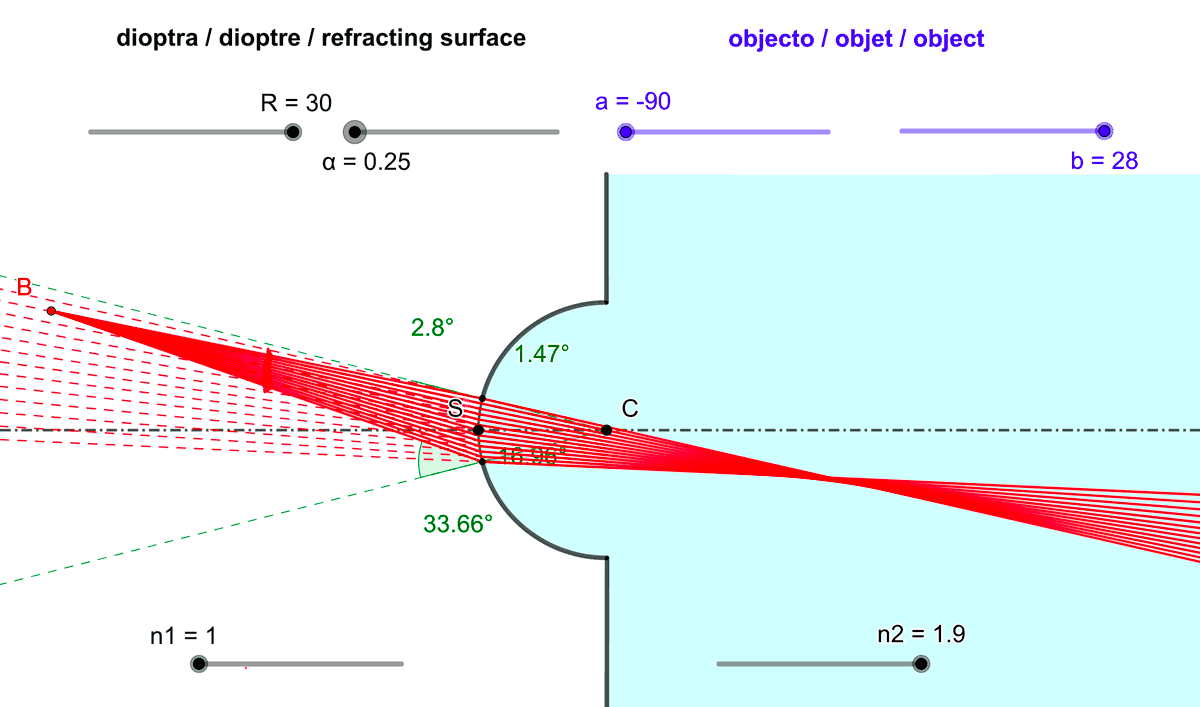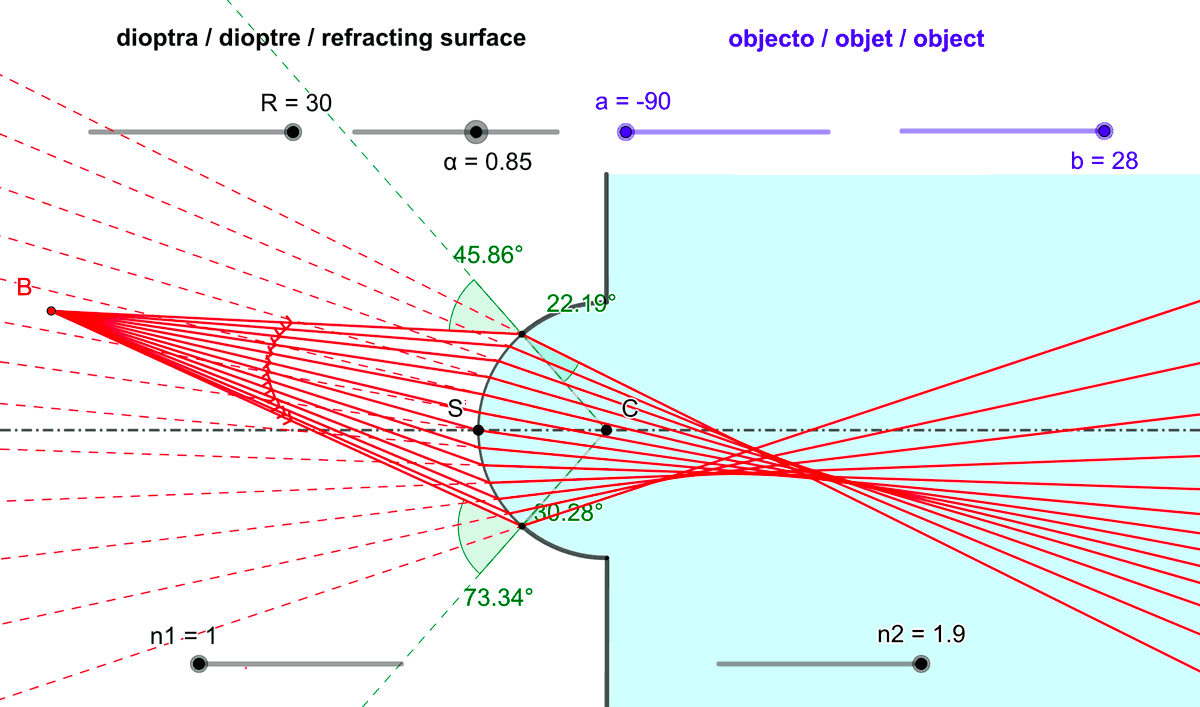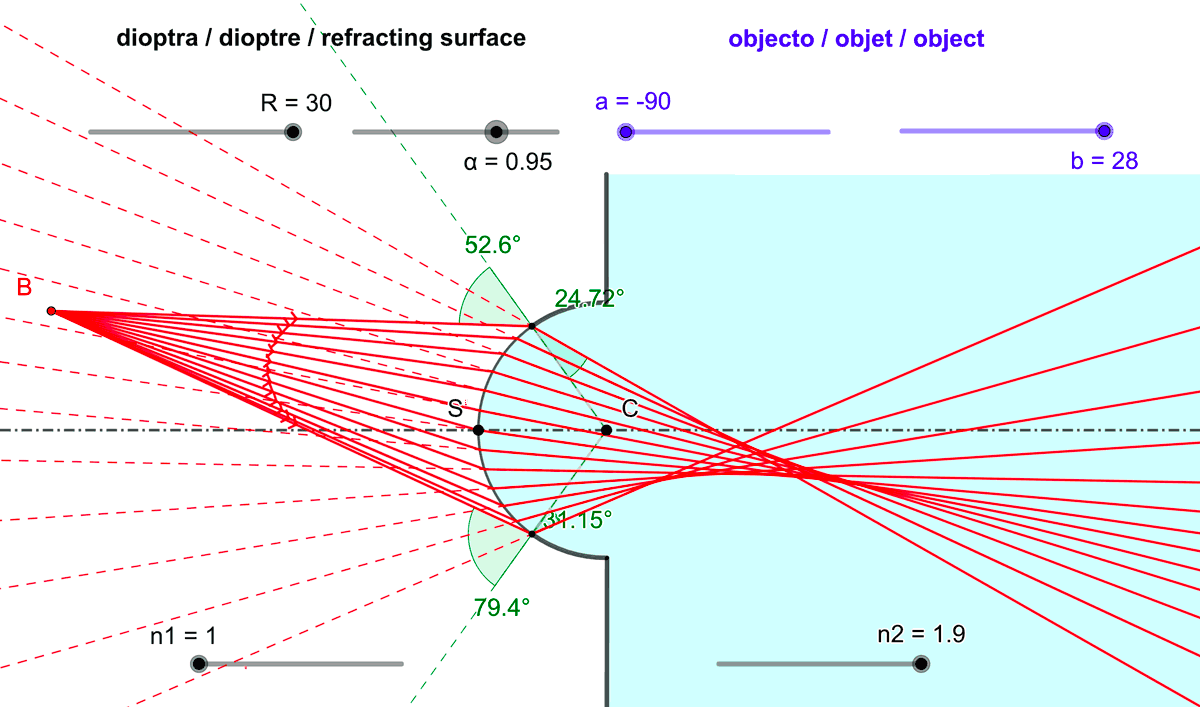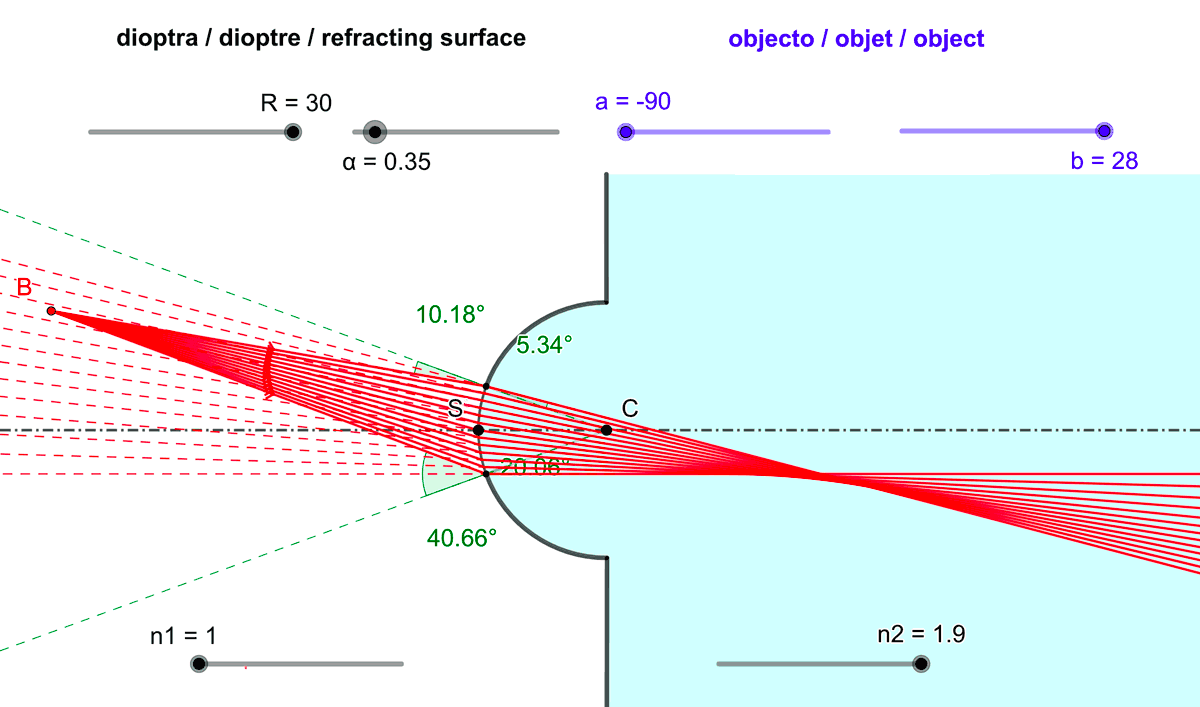
Figure 4 : Réduire l'angle d'ouverture $\alpha$ du dioptre sphérique améliore le stigmatisme.
- limiter l'observation à travers le dioptre aux points objets proches de l'axe optique.
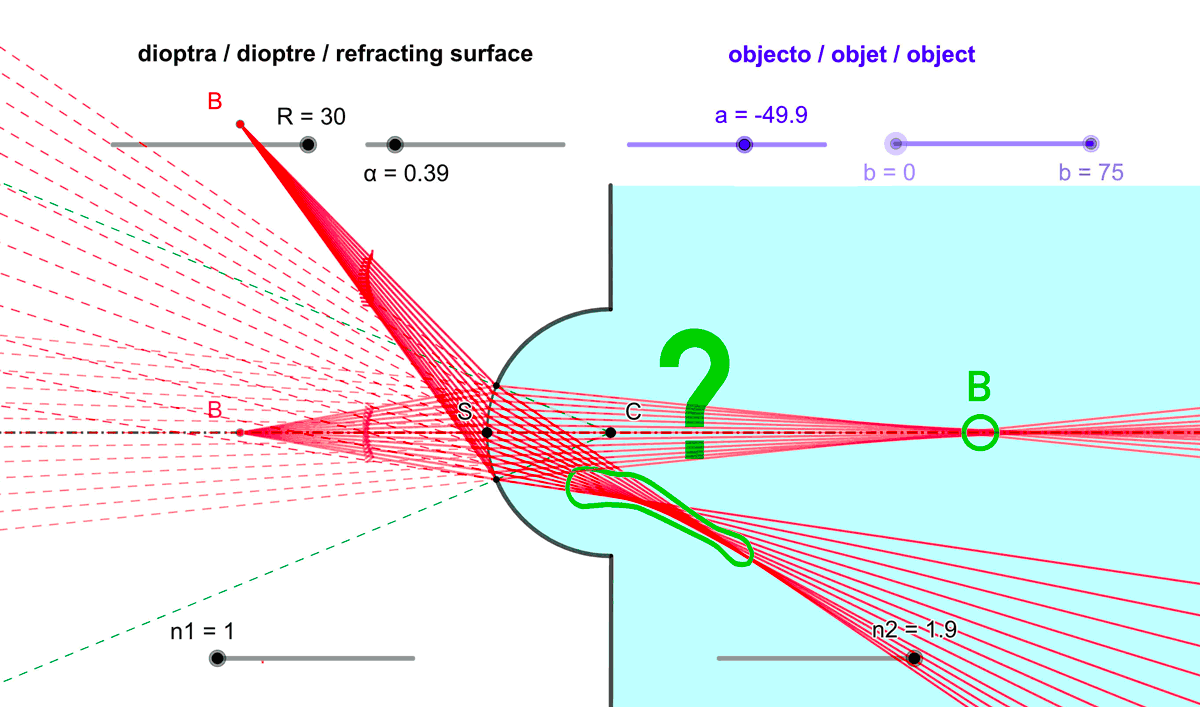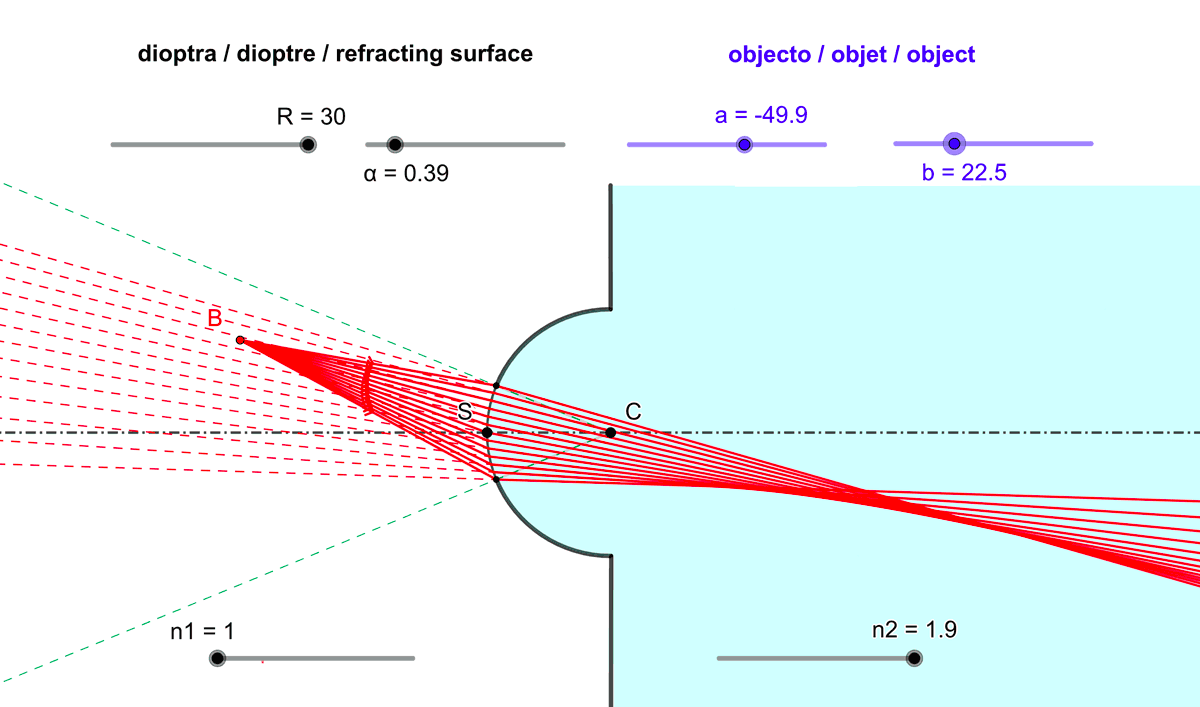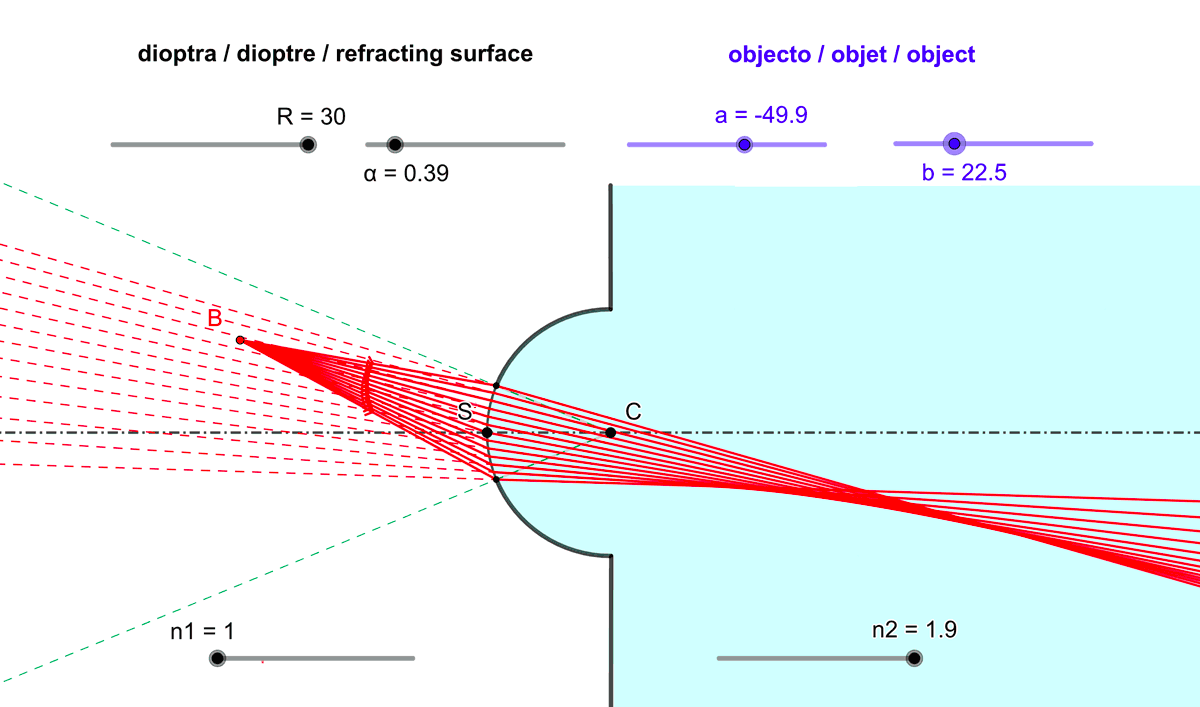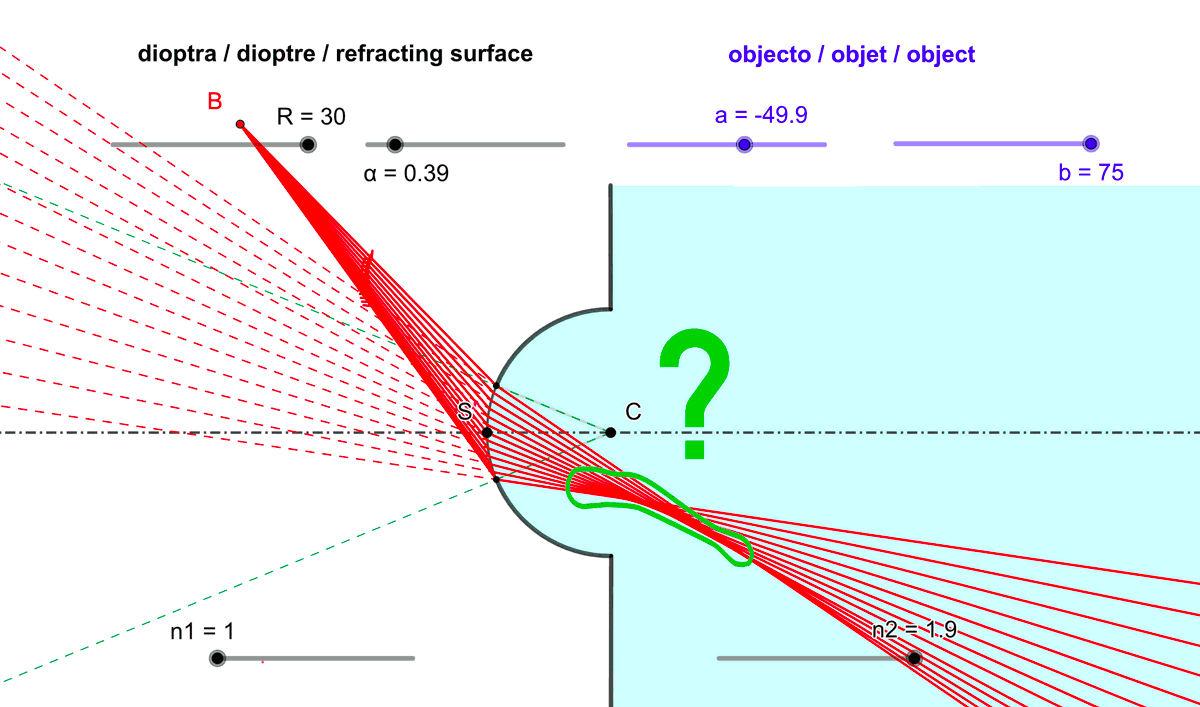Figure 5 : Limiter l'exposition du dioptre sphérique aux rayons incidents issus de points objets proches de l'axe optique améliore le stigmatisme.
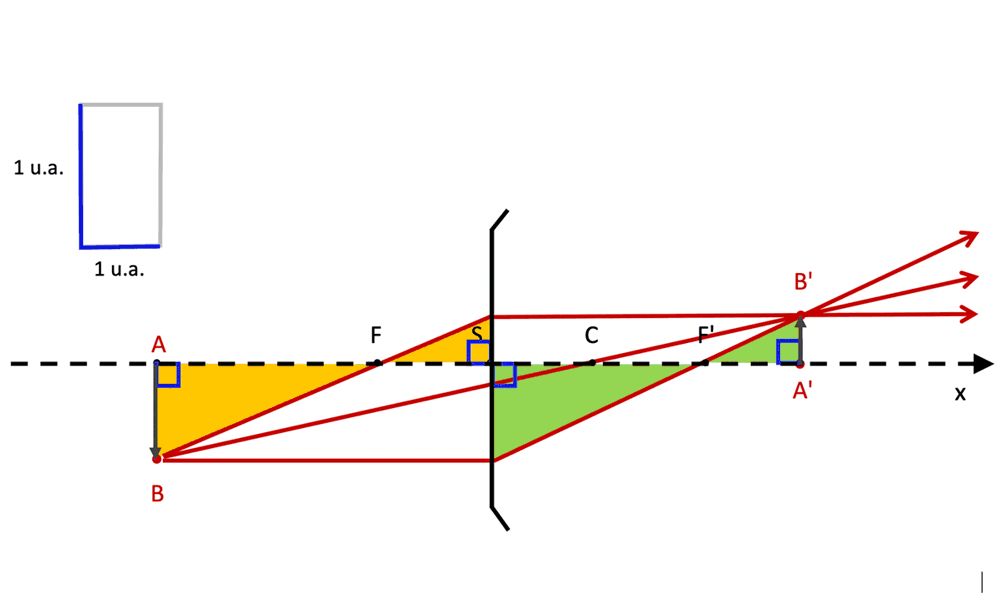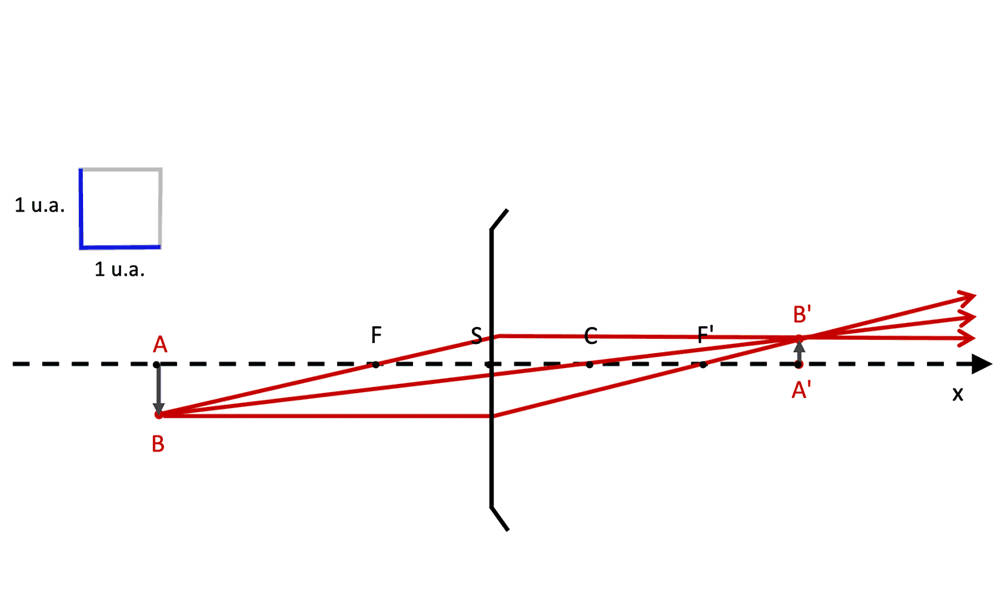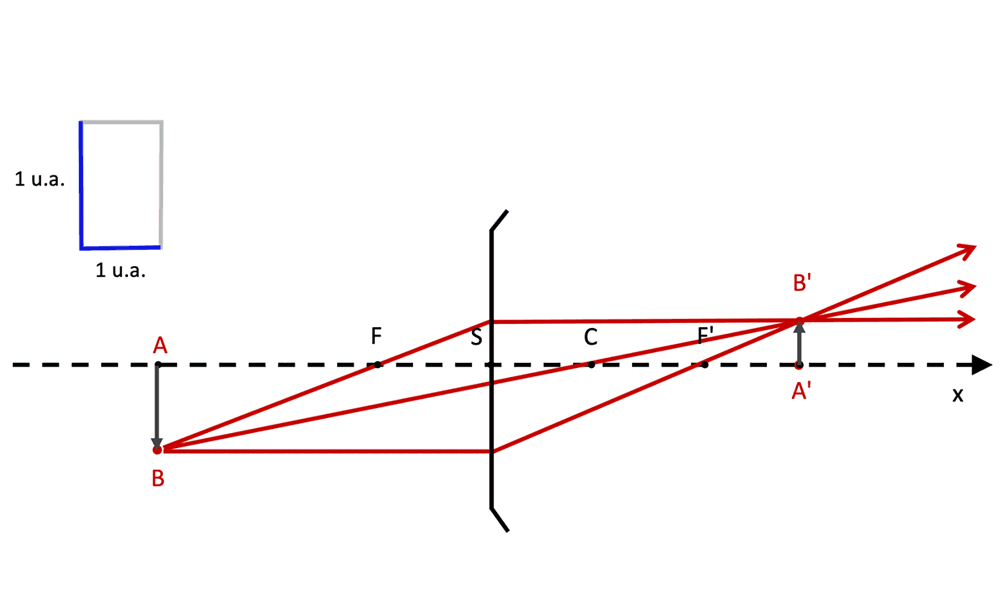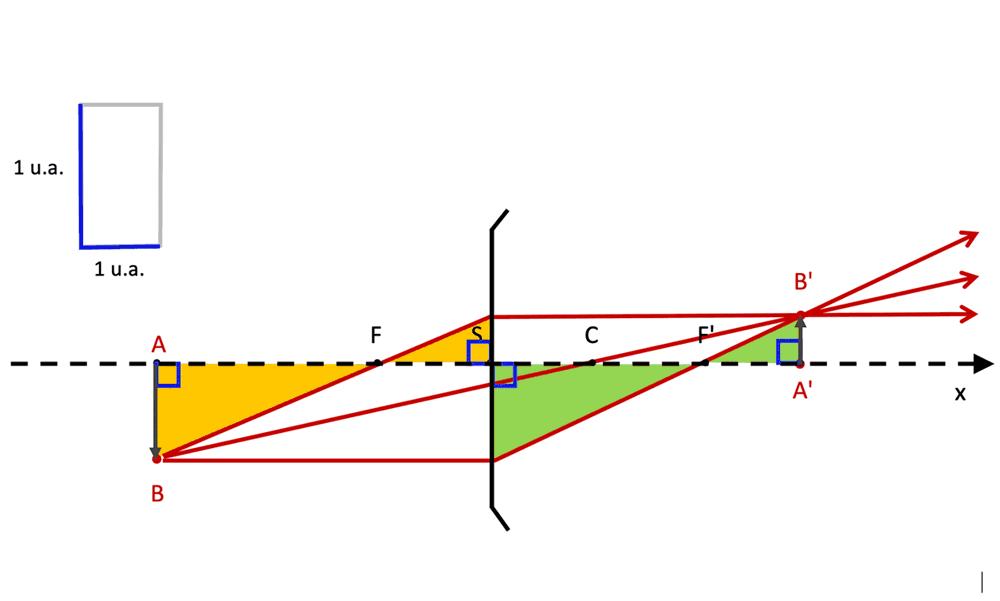
Que sont les conditions de Gauss ?
- conditions de Gauss = conditions de l'optique paraxiale
blablablz
Comment savoir si les conditions de Gauss sont réalisées ?
Quelles conséquences supplémentaires impliquent les conditions de Gauss ?
-
balbalbla.
-
Tous les points objets $
B_i$ situés dans un même plan perpendiculaire à l'axe optique appelé plan objet, et qui traversent le système optique en respectant les conditions de Gauss, donnent des points images situés "dans" ou "au voisinage" d'un même plan perpendiculaire à l'axe optique appelé plan image. -
point objet B et son point image B' sont appelés points conjugués par le sysytème optique.
-
point objet du oint objet B et pla image du point image conjugué de B sont appelés plans conjugués par le sysytème optique.
-
blablabla, gros paragraphe là (dans partie "principale"), on va pouvoir utiliser traingles rectangles, Thalès, faire de la géométrie, d'où le nom :
optique paraxiale = optique gaussienne
Que signifie passer de l' Optique des rayons à l' Optique gaussienne ?
C'est un modèle qui ...
Qu'est-ce que "les aberrations optiques" ?
Elles décrivent, par catégorie, les écarts entre le comportement réel de la lumière décrit dans le cadre de l'optique des rayons, et prévisions données par l'optique paraxiale.
blablabla, à refaire.