6.2 KiB
| title | media_order |
|---|---|
| The thin lens | Const_lens_conv_point_AapresO.gif,lens-convergent-N2-en.jpeg,Const_lens_conv_point_AentreFO.gif,lens-convergent-N2-es.jpeg,lens-convergent-N2-fr.jpeg,Const_lens_conv_point_AavantF.gif,lens-divergent-N2-es.jpeg,lens-divergent-N2-fr.jpeg,lens-divergent-N2-en.jpeg,diverging-thin-lens-representation.jpeg,converging-thin-lens-representation.jpeg |
What is a lens ?
Objective
- initial : to focuse or disperse the light.
- ultimate : to realize images, alone or as part of optical instruments.
Physical principle
- uses the refractive phenomenon, described by the Snell-Descartes' law.
Constitution
- Piece of glass, quartz, plastic (for visible and near infrared and UV).
- Rotationally symmetrical.
- 2 polished surfaces perpendicular to its axis of symmetry, either or both curved (and most often spherical).
Interest in optics : thin lenses
- Thin lens : thickness << diameter
- Thins lens : most important simple optical element that is used alone or combined in serie in most optical instruments : magnifying glasses, microscopes, tele and macro objectives, camera, refracting telescopes.
Modeling a thin lens surrounded by air, gaz or vaccum.
Why modeling ?
- To understand, calculate and predict images of objects given by thin lenses
Why surrounded by air, gaz or vaccum?
- In most optical instruments, lenses are surrounding by air.
- air, gaz and vaccum have refractive index values in the range "$1.000\pm0.001$, and can be approximated by *$n_{air}=n_{gaz}=n_{vaccum}=1$*
$\Longrightarrow$ same optical behavior in air, gaz and vacuum.
Types and characterization of thin lenses
Convergent = converging = convexe = positive lenses
- Characterized by :
- Focal lenght (usually in cm) always >0 + adjective "converging"
or
- Its image focal length $f'$ (in algebraic value, usually in cm), that is positive $f'>0$.
or
- Its vergence $V$ (in ophtalmology) that is positive $V>0$,
with $V (\delta)=\dfrac{1}{f'(m)}$ ($f'$ being expresssed in m "meter" and $V$ in $\delta$ "dioptre", so $\delta=m^{-1}$).
Divergent = diverging = **concave ** = negative lenses
- Characterized by :
- Focal lenght (usually in cm) always >0 + adjective "diverging"
or
- Its image focal length $f'$ (in algebraic value, usually in cm), that is negative $f'<0$.
or
- Its vergence $V$ (in ophtalmology) that is negative $V<0$,
with $V (\delta)=\dfrac{1}{f'(m)}$ ($f'$ being expresssed in m "meter" and $V$ in $\delta$ "dioptre", so $\delta=m^{-1}$).
Analytical modeling
(for thin lens surrounded by air, gaz or vaccum)
Thin lens equation
$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=V=-\dfrac{1}{\overline{OF}}=\dfrac{1}{\overline{OF'}}$
Transverse magnification expression
**$M_{T-thinlens}=\dfrac{\overline{OA'}}{\overline{OA}}$**
Graphical modeling
Thin lens representation
-
optical axis = revolution axis of the lens, positively oriented in the direction of propagation of the light (from the object towards the lens).
-
thins lens representation :
- line segment, perpendicular to optical axis, centered on the axis with symbolic indication of the lens shape at its extremities (convexe or concave).
- S = C = O : vertex S = nodal point C = center O of the thin lens $\Longrightarrow$ is used point O.
- point O, intersection of the line segment with optical axis.
- object focal point F and image focal point F', positioned on the optical axis symmetrically with respect to the point O ($f=-f'$) at algebraic distances $\overline{OF}=f$ and $\overline{OF'}=f'$.
- object focal plane (P) and image focal plane (P'), planes perpendicular to the optical axis at respectively points $F$ and $F'$.
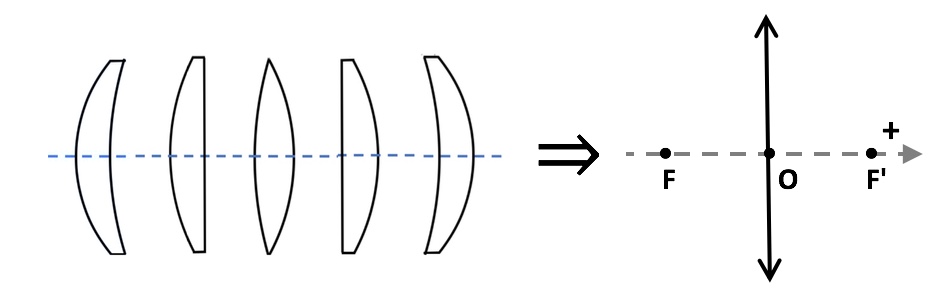
Converging thin lens representation : $\overline{OF}<0$ , $\overline{OF'}>0$ and $|\overline{OF}|=|\overline{OF'}|$
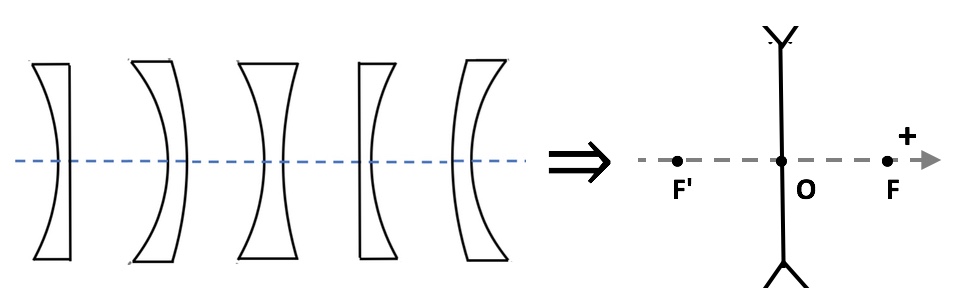
Divverging thin lens representation : $\overline{OF}>0$ , $\overline{OF'}<0$ and $|\overline{OF}|=|\overline{OF'}|$
Determining conjugate points :
Converging thin lens
Towards geogebra animations :
- Graphical construction
Click here for geogebra animation
- Graphical construction and light pencils
Click here for geogebra animation
- Graphical construction and transverse magnification
Click here for geogebra animation
- Point source located between ∞ et F
- Point source located between F et O
- Virtual object point (will be seen at level foothills, to remove from here).
Diverging thin lens
(to be implemented)